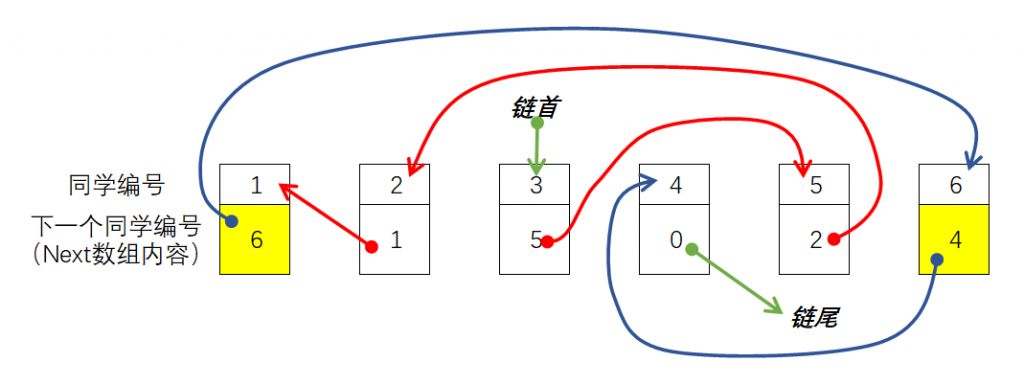
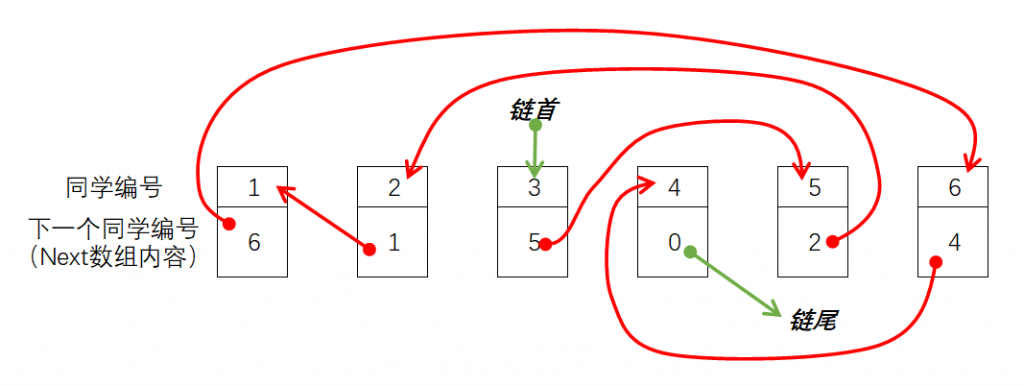
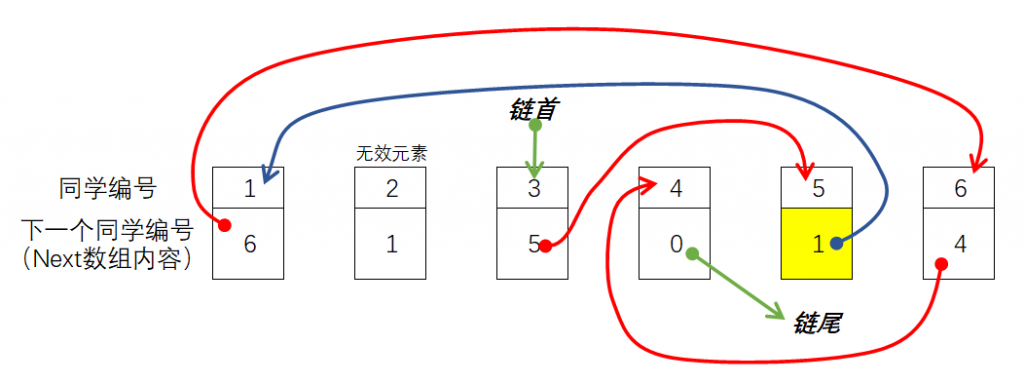
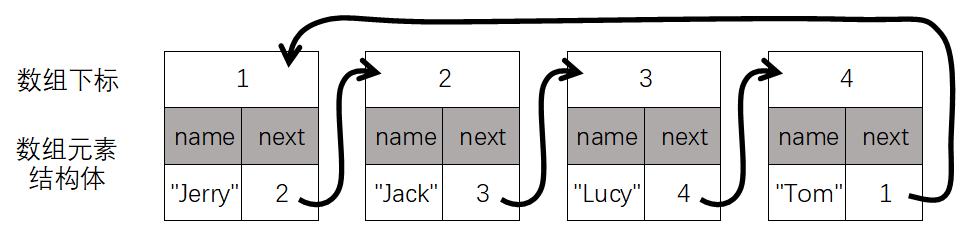
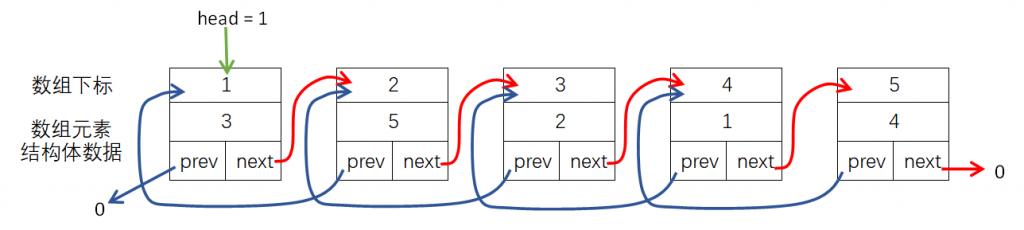
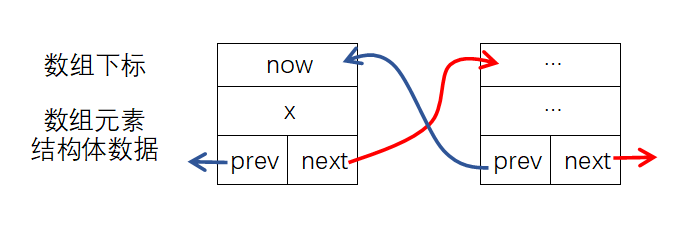
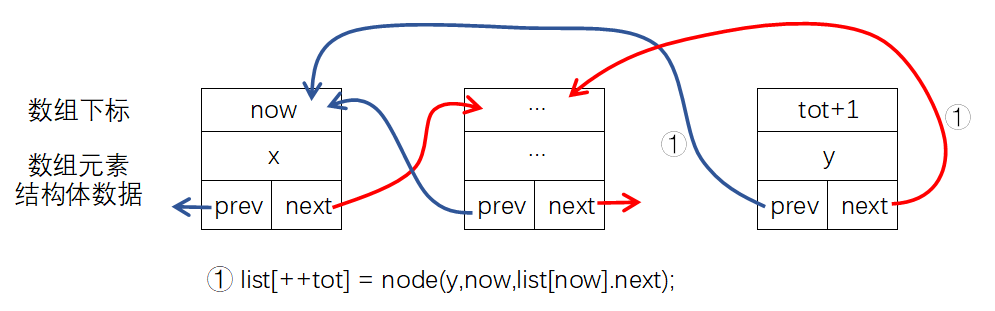
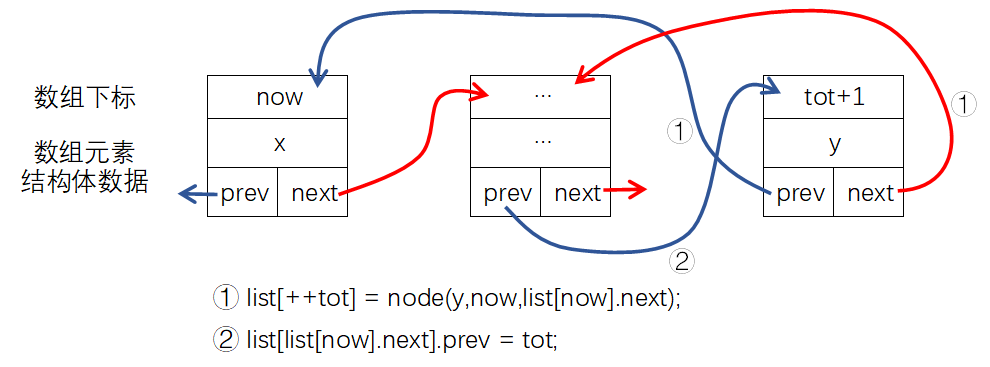
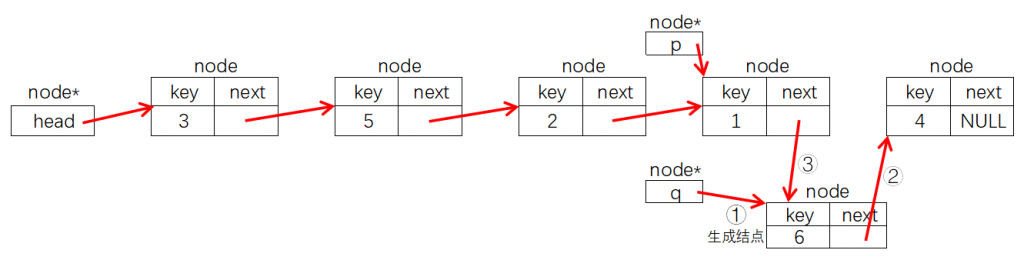
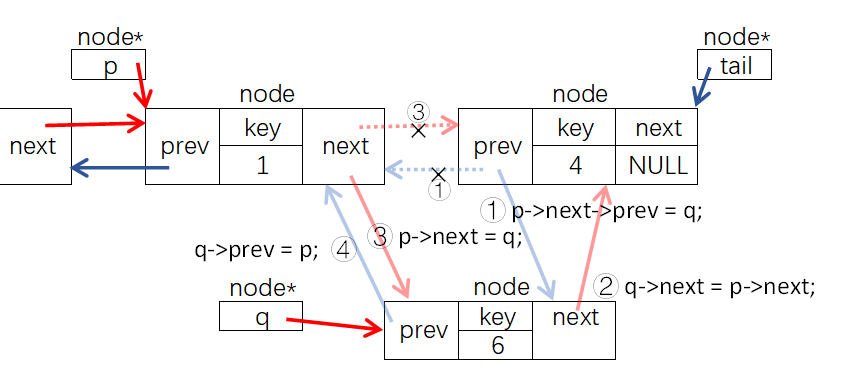
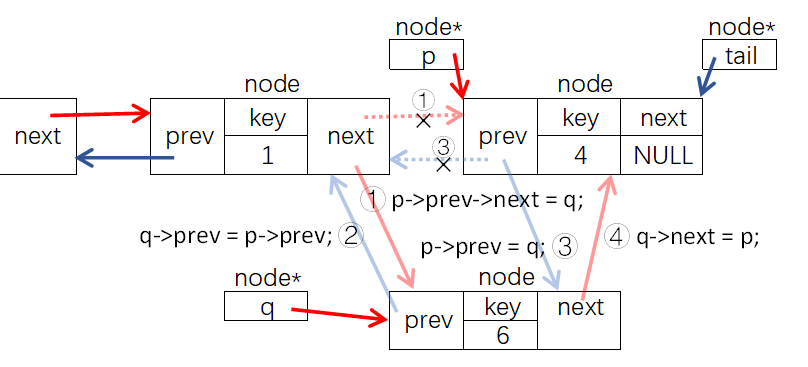
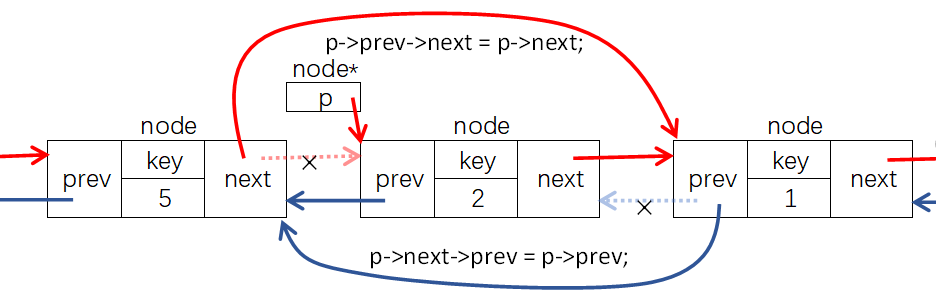
线性表是最简单、最基本的一种数据结构,线性表可以描述为若干具有相同数据类型的数据按照线性“串起来”的结构,线性表中的每个元素都有前一个元素(前驱)和后一个元素(后继)。线性表可以分为栈、队列、链表等。
一、栈的定义
先来看一个例子:小张是流水线上的检验工人,他的工作是将传送带送来堆叠在一起的薄片零件从上到下依次取出检验。在他检验的过程中,还有大量的零件源源不断的传送过来,新传送来的零件堆在最上面。在工作的前半段时间,传送带传送零件的速度会快于小张的检验速度。
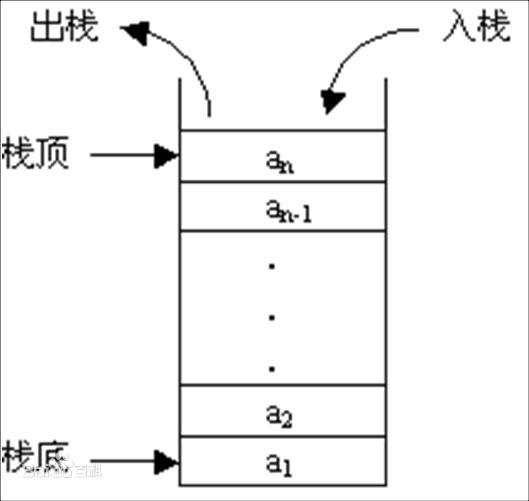
仔细分析我们会发现,每次新来的零件放在最上面,每次拿走检验的也是最上面的零件,但是由于检验速度慢一些,所以会造成零件逐渐积压。在这个过程中,每次检验的都是最新传送来的零件。这个例子表现出来的数据结构就是栈。栈是一种后进先出(LIFO——last in first out)的线性表,其特点是只允许在线性表的一端(称为栈顶)插入元素(称为入栈)和删除元素(称为出栈)。
二、栈的实现
可以使用“数组+函数”来模拟栈和栈的一些操作:入栈、出栈、取栈顶元素、判断栈是否为空等:
#include<iostream>
using namespace std;
const int MAX = 10000;
int stack[MAX];
int top = -1; //栈顶“指针”,也就是栈顶对应数组的下标
void push(int n){ //入栈(没有考虑数组已经被存满时不能入栈的情况)
stack[++top] = n;
}
void pop(){ //出栈(没有考虑栈为空时不能出栈的情况)
top--;
}
int getop(){ //取栈顶元素(没有考虑栈为空时不能取栈顶元素的情况)
return stack[top];
}
bool empty(){ //判断栈是否为空
return top==-1;
}
void print(){ //依次输出从栈底到栈顶的元素(测试需要)
for(int i=0;i<=top;i++) cout<<stack[i]<<" ";
cout<<endl;
}
int main()
{
for(int i=1;i<=5;i++) push(i);
print();
cout<<getop()<<endl;
pop();
print();
push(6);push(7);
print();
while(!empty()){ //全部出栈
cout<<getop()<<endl;
pop();
}
return 0;
}
三、经典例题
1.P1739 表达式括号匹配
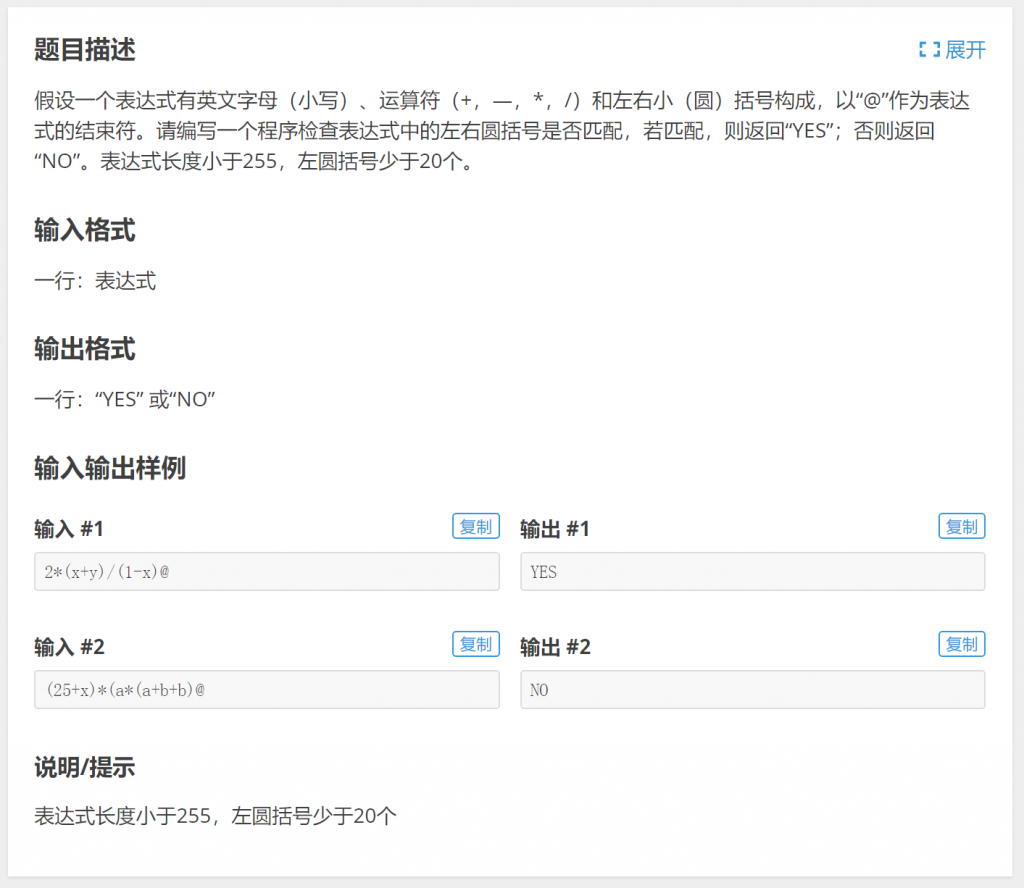
分析:使用栈来处理,依次扫描表达式中的字符,碰到左括号入栈,碰到右括号出栈。如果发现栈为空时要出栈的情况,或者扫描结束后栈不为空,那么括号不匹配。
#include<iostream>
using namespace std;
const int MAX = 300;
int stack[MAX];
int top = -1; //栈顶“指针”,也就是栈顶对应数组的下标
void push(int n){ //入栈(没有考虑数组已经被存满时不能入栈的情况)
stack[++top] = n;
}
int pop(){ //出栈(不仅仅出栈还返回出栈元素,没有考虑栈为空时不能出栈的情况)
return stack[top--];
}
bool empty(){ //判断栈是否为空
return top==-1;
}
int main()
{
char ch;
while(cin>>ch){
if(ch=='(') push(1); //入栈(入栈的数据在本题意义不大)
else if(ch==')'){
if(empty()){ //该出栈却发现栈为空,肯定不匹配
cout<<"NO";
return 0;
}
pop(); //出栈
}
}
//扫描结束后,栈为空则匹配
if(empty()) cout<<"YES";
else cout<<"NO";
return 0;
}
本问题较简单,不使用栈也能处理。可以记录扫描过程中遇到的左括号的数量,遇到左括号计数+1,遇到右括号计数-1:
#include<iostream>
using namespace std;
int main()
{
char ch;
int cnt = 0;
while(cin>>ch){
if(ch=='(') cnt++;
else if(ch==')'){
if(cnt==0){
cout<<"NO";
return 0;
}
cnt--;
}
}
if(cnt==0) cout<<"YES";
else cout<<"NO";
return 0;
}
2.P1241 括号序列

分析:仍然使用栈来找出所有“找不到与之配对的括号”。对于这些没有与之配对的括号,如果是左括号,紧跟着左括号添加对应右括号;如果是右括号,在前面添加上对应左括号即可(下面的代码没有用函数来实现栈的操作)。
#include<iostream>
using namespace std;
struct node{
char ch;
int pos;
node(){}
node(char ch,int pos){
this->ch = ch;
this->pos = pos;
}
};
const int MAX = 110;
node stack[MAX];//栈里元素是结构体,记录字符和序号
int top = -1; //栈顶“指针”
char b[MAX]; //原始字符
int c[MAX]; //标记每个字符的匹配情况:0匹配,1不匹配
int main()
{
int i = 0;
while(cin>>b[i]){
if(b[i]=='(' || b[i]=='['){ //左括号:入栈
stack[++top] = node(b[i],i);
} else{
//右括号匹配上左括号,出栈
if(top!=-1 && (stack[top].ch=='(' && b[i]==')' || stack[top].ch=='[' && b[i]==']'))
top--;
else //匹配不上,标记
c[i] = 1;
}
i++;
}
while(top!=-1){ //栈里的左括号都是找不到与之匹配的,全部出栈,标记不匹配
c[stack[top--].pos] = 1;
}
for(int j=0;j<i;j++){
if(b[j]=='(' || b[j]=='['){ //左括号
cout<<b[j];
if(c[j]){ //没有匹配的右括号,直接在后面补上右括号
if(b[j]=='[') cout<<"]";
else if(b[j]=='(') cout<<")";
}
}else{ //右括号
if(c[j]){ //没有匹配的左括号,直接在前面补上左括号
if(b[j]==']') cout<<"[";
else if(b[j]==')') cout<<"(";
}
cout<<b[j];
}
}
return 0;
}
四、*利用结构体实现栈
【选择阅读】也可以将栈封装成一个结构体,在结构体里使用成员函数实现栈的功能,通过调用结构体变量的成员函数实现入栈、出栈、判断栈是否为空:
#include<iostream>
using namespace std;
//用结构体封装栈
const int N = 10000;
struct stack{
int pool[N];
int top;
stack(){ //构造函数
top = -1;
}
//判断栈是否为空
bool empty(){
return top==-1;
}
//入栈(如果存放栈元素的数组已满,返回false)
bool push(int n){
if(top>=N) return false;
pool[++top] = n;
return true;
}
//出栈(如果栈为空,返回false)
bool pop(){
if(empty()) return false;
top--;
return true;
}
//获取栈顶元素(如果栈为空,返回一个特殊值-1)
int getop(){
if(empty()) return -1;
return pool[top];
}
};
void print(stack s){ //依次输出从栈底到栈顶的元素(测试需要)
for(int i=0;i<=s.top;i++) cout<<s.pool[i]<<" ";
cout<<endl;
}
int main()
{
stack s;
for(int i=1;i<=5;i++) s.push(i);
print(s);
if(!s.empty()) cout<<s.getop()<<endl;
s.pop();
print(s);
s.push(6);s.push(7);
print(s);
while(!s.empty()){ //全部出栈
cout<<s.getop()<<endl;
s.pop();
}
return 0;
}
 NOIP学习小站
NOIP学习小站