再谈变量的使用

变量用来存储数据，变量的值在程序中可以通过输入语句或者赋值语句来赋值，并且可以按照需求多次给变量重新赋值，这正是变量一词中“变”的由来。在实际编程时，可以利用变量的这一特征来持续“追踪”变化的状态。

1.猴子吃桃

一只猴子有若干桃子。第一天它吃了这些桃子的一半以后，又贪嘴多吃了一个；第二天它也吃了剩余桃子的一半，又贪嘴多吃了一个；第三天它又吃了剩余桃子的一半，并贪嘴多吃了一个。第四天起来一看，只剩下 n 个桃子了。问：猴子最开始有多少个桃子？

【分析】直接求解问题有一定难度，不过可以从第四天倒推回去，这样就简单多了。第四天剩下 n 个桃子，那么第三天应该是 (n+1)*2 个（(n+1)*2/2-1 → n）,同理可以继续推算第二天和第一天的情况。

#include<iostream>
using namespace std;
int main()
{
	int day4,day3,day2,day1;
	cin>>day4;				//第4天 
	day3 = (day4+1)*2;		//第3天 
	day2 = (day3+1)*2;		//第2天 
	day1 = (day2+1)*2;		//第1天 
	cout<<day1<<endl;
    return 0;
} 

在倒推的过程中，可以用变量 n 一直来记录这一天猴子吃桃子前的桃子数量，第四天就是输入的 n 值，那么倒推第三天的桃子数应该是 (n+1)*2 ，直接将这个值又赋值给 n（n = (n+1)*2;），这样的话第三天的桃子数量仍然记录在变量 n 中。接着倒推第二天、第一天，仍然用这样的方法。在倒推的过程中，通过连续的赋值语句不断修改变量 n 的值，让 n 一直记录的是倒推到的天数的桃子数量，也就是用 n 来持续“追踪”倒推过程中每天的桃子数量。

#include<iostream>
using namespace std;
int main()
{
	int n;
	cin>>n;		 //第4天桃子数 
	n = (n+1)*2;	//第3天桃子数，仍然保存在n中 
	n = (n+1)*2;	//第2天桃子数，仍然保存在n中 
	n = (n+1)*2;	//第1天桃子数，仍然保存在n中 
	cout<<n<<endl;
    return 0;
} 

当然，本题也可以用数学解析法求解，可知第一天的桃子数应该是：(((n+1)*2+1)*2+1)*2，程序中直接输出即可，但这样计算表达式比较复杂，不能一下子看清楚中间的计算过程，反而还没有上面的程序可读性强。

2.分糖果游戏

#include<iostream>
using namespace std;
int main()
{
	int a,b,c,d,e,s1,s2;
	cin>>a>>b>>c>>d>>e;
	s1 = a+b+c+d+e;		//计算游戏开始前糖果总数 

	//每个小朋友分糖果导致糖果数变化，通过赋值语句重新赋值
	a/=3; e+=a; b+=a;	//第1位小朋友分糖果，a、e、b要重新赋值，三条语句写到了一行里 
	b/=3; a+=b; c+=b;
	c/=3; b+=c; d+=c;
	d/=3; c+=d; e+=d;
	e/=3; d+=e; a+=e;
	
	s2 = a+b+c+d+e;		//计算游戏结束后糖果总数
	
	cout<<a<<" "<<b<<" "<<c<<" "<<d<<" "<<e<<endl;
	cout<<s1-s2<<endl;
	return 0;
}

第二种方式就是使用累加器来累加计算吃掉的糖果总和，要注意的是累加器先要清零。

#include<iostream>
using namespace std;
int main()
{
	int a,b,c,d,e,s = 0;	//s用来计算吃掉糖果数，先清零 
	cin>>a>>b>>c>>d>>e;
	//每个小朋友分糖果导致糖果数变化，通过赋值语句重新赋值
	s+=a%3; a/=3; e+=a; b+=a;	//第1位小朋友分糖果，吃掉的糖果数a%3累加到s 
	s+=b%3; b/=3; a+=b; c+=b;
	s+=c%3; c/=3; b+=c; d+=c;
	s+=d%3; d/=3; c+=d; e+=d;
	s+=e%3; e/=3; d+=e; a+=e;
	
	cout<<a<<" "<<b<<" "<<c<<" "<<d<<" "<<e<<endl;
	cout<<s<<endl;
	return 0;
}

3.分钱游戏

#include<iostream>
using namespace std;
int main()
{
	int a,b,c,n;
	cin>>n;
	a = b = c = n/3;	//结束后三人钱数都是n/3
	 
	//逆推丙分钱前三人钱数
	//对于甲来说，他从丙那里拿到了和他已有钱相等的钱数，两份相加是a
	//那么在丙分钱之前，甲的钱数应该是a/2。乙的情况类似。
	a /= 2;			//重新赋值a，赋值后a就是丙分钱前甲的钱数 
	b /= 2;
	c = n-a-b;			//丙分钱前丙的钱数是n-a-b.也可以用 c+=a+b; 
	
	//逆推乙分钱前三人钱数
	a /= 2;
	c /= 2;
	b = n-a-c;			//也可以用 b+=a+c; 
	
	//逆推甲分钱前三人钱数
	b /= 2;
	c /= 2;
	a = n-b-c;			//也可以用 a+=b+c;
	
	cout<<a<<" "<<b<<" "<<c<<endl; 
	return 0;
}

也可以使用数学解析的方法来逆推整个过程，得出的三人钱数就是与总钱数相关的计算公式。假设总钱数为n，那么数学解析的逆推过程如下表所示：

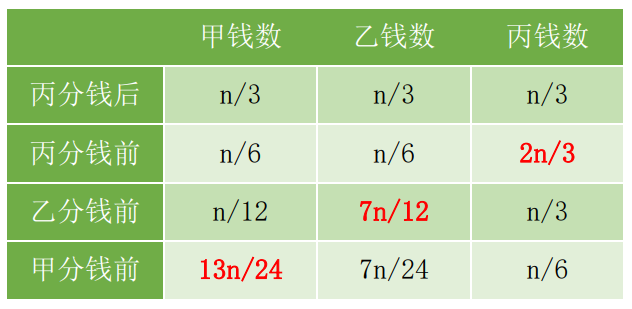
#include<iostream>
using namespace std;
int main()
{
    int n;
    cin>>n;
    cout<<13*n/24<<" ";
    cout<<7*n/24<<" ";
    cout<<n/6<<endl;
    return 0;
}