顺序结构的程序设计是最简单的,只要按照解决问题的顺序写出相应的语句就行,它的执行顺序是自上而下,依次执行。顺序结构也是最基础的,其他复杂的程序结构中都有顺序结构的影子。
一、顺序结构
顺序结构是程序设计最简单、最基础的结构,顺序结构的特点是按照解决问题的算法的详细步骤书写对应的语句,执行的时候是自上而下,依次执行。
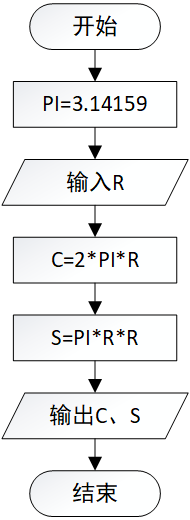
还是以计算圆的周长和面积为例:
#include<iostream>
using namespace std;
int main()
{
const double PI = 3.14159;
double r,C,S;
cin>>r;
C = 2 * PI * r;
S = PI * r * r;
cout<<C<<endl<<S<<endl;
return 0;
}
可以看出右边的代码就是将左边的算法的步骤一一依次转换成程序语句,而程序运行的时候也是按照书写的顺序从上到下依次执行语句——这就是典型的顺序结构!这个算法是按照“输入数据→计算结果→输出结果”的顺序组织的。
二、赋值语句
通过前面的学习我们已经知道,通过赋值语句可以为变量赋新值。赋值语句的格式是:\(变量名 = 表达式;\)。赋值符号 \( = \) 的作用是将右边表达式的计算结果赋值给左边的变量。赋值后变量的旧值被新值覆盖。
其实赋值语句有结果,来看一段代码:
#include<iostream>
using namespace std;
int main()
{
int n;
cout<<(n=2)<<endl; //注意()不能少,否则会出现语法错误
return 0;
}
会发现程序输出了赋值后n的值2,证明了赋值语句的结果就是变量被赋予的新值。
正因为如此,C++支持多个变量连续赋值。例如:
int a,b,c; a = b = c = 1;
此外要注意前面已经介绍过的一些特殊的赋值语句:
int n = 4,m = 6; n = n + m; n += m; //自赋值(与 n = n + m; 等效,可以认为是简写) n = n + 1; n += 1; //自赋值(与 n = n + 1; 等效,可以认为是简写) n++; //自赋值( n += 1;的简写) ++n; //自赋值( n += 1;的简写) n = n - 1; n -= 1; n--; //自赋值( n -= 1;的简写) --n; //自赋值( n -= 1;的简写)\(n++;\)与\(n++;\)几乎没有区别,特别是单独成句的时候。但是两者的执行流程不同,通过下面两段程序对比测试:
#include<iostream>
using namespace std;
int main()
{
int n,m;
n = 1;
m = n++;
cout<<n<<" "<<m;
return 0;
}
运行结果如下:
2 1\(n++;\)是先使用\(n\)的值然后\(n\)再自加1;所以\(m = n++;\),赋值语句先执行\(m = n;\),然后再执行\(n = n+1;\),最终\(n = 2\),\(m = 1\)
#include<iostream>
using namespace std;
int main()
{
int n,m;
n = 1;
m = ++n;
cout<<n<<" "<<m;
return 0;
}
运行结果如下:
2 2\(++n;\)是\(n\)先自加1然后再使用\(n\)的值,所以\(m = ++n;\),赋值语句先执行\(n = n+1;\),然后再执行\(m = n;\),最终\(n = 2\),\(m = 2\)
三、经典顺序结构
1.交换器
如何交换两个变量a、b的值?注意:是真正的在计算机内部的值交换,而不是“输入a、b;输出b、a”这样的障眼法。你可能会想到这样:
#include<iostream>
using namespace std;
int main()
{
int a,b;
cin>>a>>b;
cout<<a<<" "<<b<<endl;
a = b;
b = a;
cout<<a<<" "<<b<<endl;
return 0;
}
#include<iostream>
using namespace std;
int main()
{
int a,b;
cin>>a>>b;
cout<<a<<" "<<b<<endl;
b = a;
a = b;
cout<<a<<" "<<b<<endl;
return 0;
}
很显然,上面的两段代码都不能实现交换a、b的值,左边代码导致a、b的值都变成原来b的值,右边的代码导致a、b的值都变成原来a的值。很显然a=b、b=a这样简单的赋值不能实现交换,那试试下面的代码:
#include<iostream>
using namespace std;
int main()
{
int a,b,c,d;
cin>>a>>b;
cout<<a<<" "<<b<<endl;
c = a;
d = b;
a = d;
b = c;
cout<<a<<" "<<b<<endl;
return 0;
}
思路是用两个变量c、d分别赋值成a、b的值(相当于在接下来要修改a、b的值之前把a、b的值保存到其它的变量中,存了一个副本一样),然后就可以放心大胆地修改a、b的值而不用担心a、b原来的值无法找回来(在变量c、d里保存着),然后执行赋值语句\(a = d;\) \(a\)的值变成了\(d\)(也就是原来的\(b\)),执行赋值语句\(b = c;\) \(b\)的值变成了\(c\)(也就是原来的\(a\))。
注意体会这里的算法,要修改变量的值,并且修改后还要用到变量修改前的旧值,可以借助额外的变量在修改之前把旧值保存下来。
其实这里并不需要两个额外的变量来保存a、b的值,用1个变量就行:
#include<iostream>
using namespace std;
int main()
{
int a,b,t;
cin>>a>>b;
cout<<a<<" "<<b<<endl;
t = a;
a = b;
b = t;
cout<<a<<" "<<b<<endl;
return 0;
}
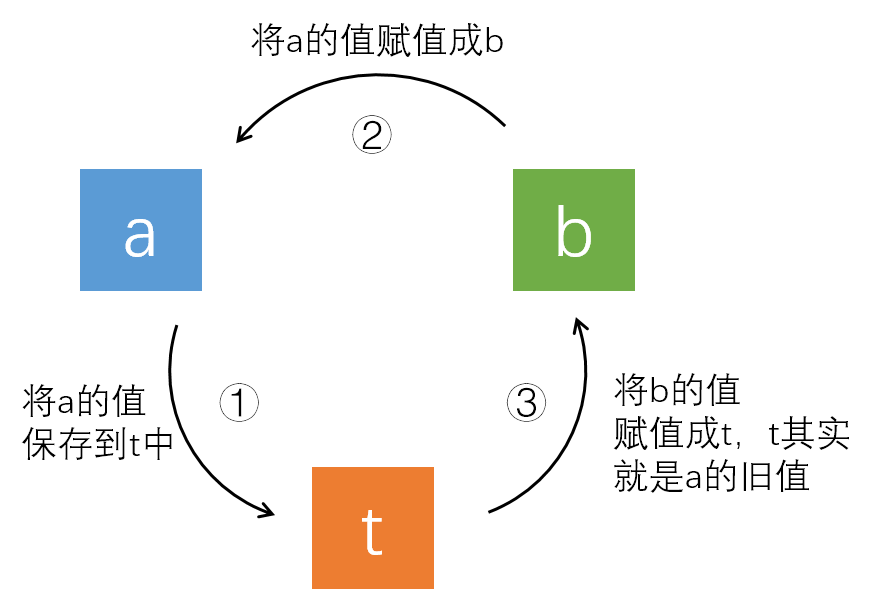
再来试试下面的代码,不借助额外的变量,靠简单的加减运算也能实现交换:
#include<iostream>
using namespace std;
int main()
{
int a,b;
cin>>a>>b;
cout<<a<<" "<<b<<endl;
a = a+b;
b = a-b;
a = a-b;
cout<<a<<" "<<b<<endl;
return 0;
}
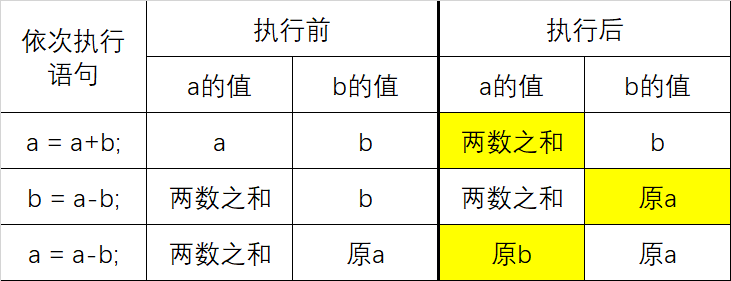
这一个精心设计的算法,没有用到额外的变量,却很巧妙地实现了交换。看吧,这就是算法的魅力!
2.计数器
现在想统计一下参加兴趣小组活动的同学的数量,现实生活中最简单的做法是报数,我们也能借助程序来模拟报数的过程:
#include<iostream>
using namespace std;
int main()
{
//变量tot用来报数(计数)
int tot = 0; //初始值0
//第1个同学报数
tot++;
cout<<tot<<endl;
//第2个同学报数
tot++;
cout<<tot<<endl;
//第3个同学报数
tot++;
cout<<tot<<endl;
//后面的同学依次报数
//...
return 0;
}
左边的程序“每位同学都报数了”,当然最后报数就是人数。也可以只在最后输出tot变量,实现真正的“计数”,而不是每位同学都报数:
#include<iostream>
using namespace std;
int main()
{
int tot = 0;
tot++;
tot++;
tot++;
//...
//每一位同学报数其实就是执行一次tot++;
cout<<tot<<endl;
return 0;
}
3.累加器
再来看一个问题,统计同学们捐献的爱心图书数量。我们也可以借助“计数器”的思路实现,不过计数器每次累加的都是1,而这里可能是任意的整数(每位同学捐献的图书数量不一定都是1本):
#include<iostream>
using namespace std;
int main()
{
int s = 0; //初值0
//第1位同学捐献爱心图书5本
s += 5;
//第2位同学捐献爱心图书2本
s += 2;
//第3位同学捐献爱心图书1本
s += 1;
//...
//对于每位同学,s累加上捐献图书本数
cout<<s<<endl;
return 0;
}
左边的程序结构称之为累加器,通过多条赋值(自赋值)语句不停地将数累加到变量s上,最后s就是所有数的和。
可知,计时器是累加器的特例:每次累加的数都是1。
不过要记住,对于计数器和累加器变量,最开始一般要赋初值0。
这里还看不出来计数器和累加器的实用价值,等后面学习了循环结构,借助循环语句它们的实用性就能充分体现出来。
4.累乘器
和前面的计数器、累加器相似,累乘器实现的效果是重复将一个数放大若干倍数,例如要计算5的阶乘(\(n!=1 \times 2 \times 3 \times ... \times n\)),使用累乘器代码如下:
#include<iostream>
using namespace std;
int main()
{
int t = 1; //初值为1
t *= 2;
t *= 3;
t *= 4;
t *= 5;
cout<<t<<endl;
return 0;
}
同样地,这里还看不出来累乘器的实用价值,等后面学习了循环结构,借助循环语句它们的实用性就能充分体现出来。
 NOIP学习小站
NOIP学习小站