if语句的嵌套-NOIP学习小站

前面一小节介绍了if语句的基本使用方法，其中条件的描述从最简单的单一数据、简单的关系表达式，再到复杂的多条件复合逻辑运算。本小节我们主要学习if语句的嵌套，也就是if语句的if子句部分或者else子句部分中又出现if语句的结构。

通过前一小节的学习，我们已经知道，选择结构下的if语句对应的是两种对立情况的分类讨论。如果要处理的问题需要分更多的情况来分类处理，很显然此时简单的if语句是无法满足的，这个时候可以使用本小节介绍的if语句的嵌套结构来解决问题。

先来看一个简单的问题：输入一个整数$n$，输出这个整数的符号（0或者+或者-）。

很明显，这里可以分三种情况讨论：

如果$n>0$，输出+；
如果$n==0$，输出0；
如果$n<0$，输出-；

这里的三种情况是“互斥”的（对于一个整数$n$，只能满足三种情况的一个条件，不可能满足这三种情况中的多个条件），所以这里可以使用三个先后顺序的if语句来解决问题：

#include<iostream>
using namespace std;
int main()
{
	int n;
	cin>>n; 
	if(n>0) cout<<"+"<<endl; 
	if(n==0) cout<<"0"<<endl;
	if(n<0) cout<<"-"<<endl;
	return 0;
}

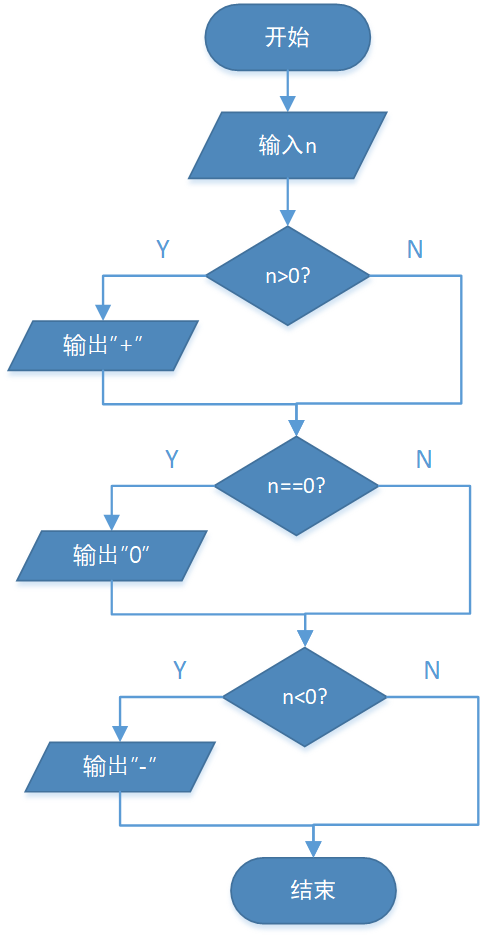
算法的流程图如下左图所示：

其实算法还可以这样设计：

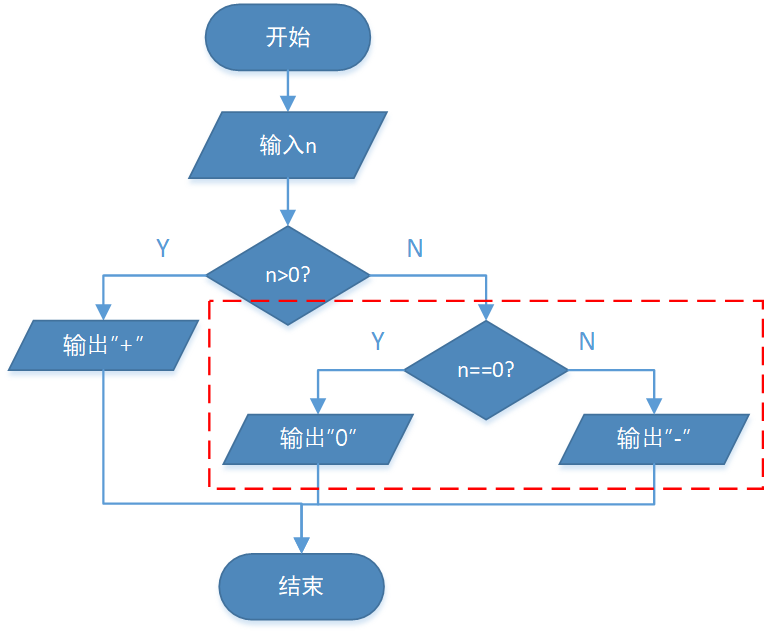
我们注意上面流程图中用红色虚线标注出来的选择结构，这个选择结构属于外层选择结构条件不成立的部分。像这样的选择结构内部又包含了选择结构的情况，称为选择结构的嵌套。

使用if语句的嵌套解决上述问题参考代码如下：

#include<iostream>
using namespace std;
int main()
{
	int n;
	cin>>n;
	if(n>0){
		cout<<"+";
	}else{	//这里的else意味着n<=0 
		if(n==0){
			cout<<"0";
		}else{
			cout<<"-";
		}
	}
	return 0;
}

#include<iostream>
using namespace std;
int main()
{
	int n;
	cin>>n;
	//下面的嵌套结构和上面流程图不同，请自行分析
	if(n>=0){
		if(n==0){
			cout<<"0";
		}else{
			cout<<"+";
		}
	}else{
		cout<<"-";
	}
	return 0;
}

一、if语句的嵌套与多分支结构

再来看一个稍微复杂的问题，计算三个整数$a,b,c$的最大值。

如果使用前面介绍的$max$函数，那么可以这样处理：

#include<iostream>
using namespace std;
int main()
{
	int a,b,c,t;
	cin>>a>>b>>c;
	t = max(a,b);
	cout<<max(t,c);
	return 0;
}

#include<iostream>
using namespace std;
int main()
{
	int a,b,c;
	cin>>a>>b>>c;
	//将max函数的计算结果作为另一个max函数的参数
	cout<<max(max(a,b),c);
	return 0;
}

思路：分类讨论，可以分以下三种情况讨论：

a>b && a>c：此时最大值是a；
b>a && b>c：此时最大值是b；
其它情况：最大值是c。

从前一小节可知，简单的if语句只能用于两种情况的分类讨论（条件成立或者不成立两种情况），这里有三种情况，怎么用if语句实现呢？

其实还可以这样分类讨论：

a>b && a>c：此时最大值是a;
其它情况。这里可以再分类讨论：
1. b>a && b>c：此时最大值是b；
2. 其它情况：最大值是c。

可以看出，思路是将情况1单独拿出来，剩余的情况看成一个整体（此时只有两种情况：情况1、情况2和情况3的组合）；然后又可以从剩余的情况中再取出来一种情况（原来的情况2），剩余的情况又可以看成一个整体（此时仍然只有两种情况，不过这里剩余的就是一个简单情况——原来的情况3）。

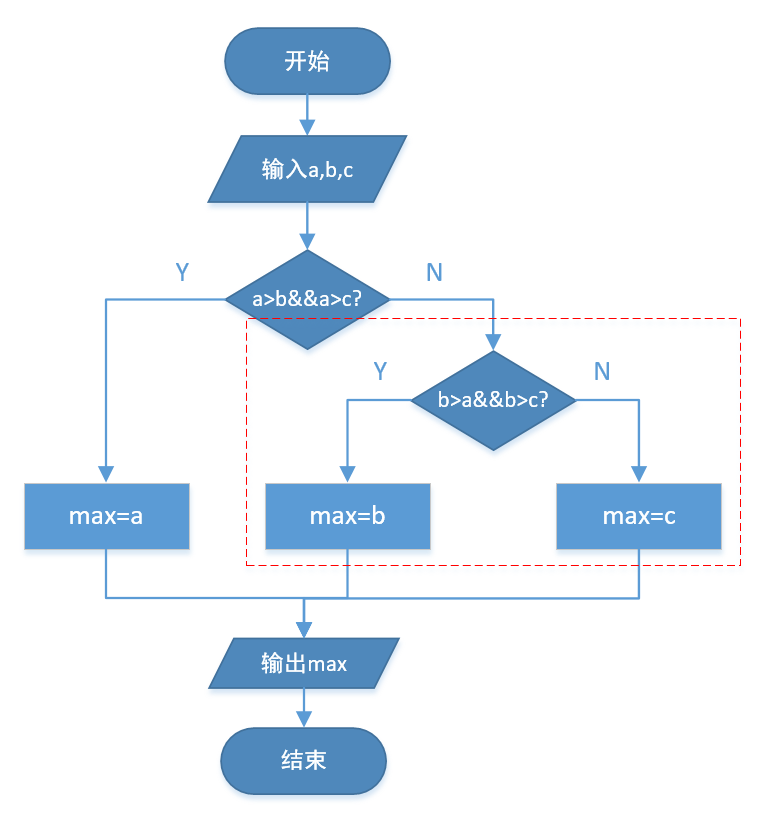
流程图如右图所示：

可以预见，在第一次判断if语句的else部分（图中虚线框部分）又会出现一个完整的if语句。

完整的代码如下：

#include<iostream>
using namespace std;
int main()
{
	int a,b,c,max;
	cin>>a>>b>>c; 
	if(a>b && a>c){
		max = a;
	}else{
		//else部分又是一个if语句
		//这种情况称为 if语句的嵌套
		if(b>a && b>c){
			max = b;
		}else{
			max = c;
		}
	}
	cout<<max<<endl;
	return 0;
}

左边外层if的else部分是一个整体，{}省略并将内容与else写到一行的效果如下：

#include<iostream>
using namespace std;
int main()
{
	int a,b,c,max;
	cin>>a>>b>>c; 
	if(a>b && a>c){
		max = a;
	}else if(b>a && b>c){
		max = b;
	}else{
		max = c;
	}
	cout<<max<<endl;
	return 0;
}

对于更多情况的分类讨论，思路一致，每次从剩余情况中分出一种，流程图如下：

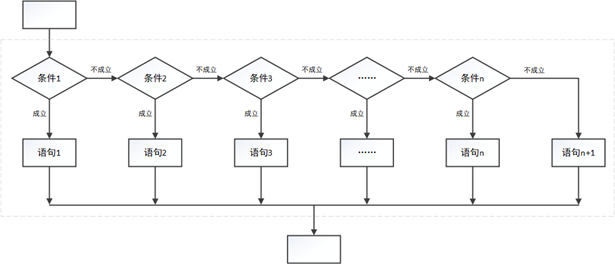
可知上面多分支结构的流程图执行过程如下：从左往右（从代码角度看是从上往下）先后判断每个条件是否成立：如果某个条件成立，那么执行该分支的语句，然后退出整个多分支结构（后续的判断也就不会被执行了）；如果所有条件都不成立，那么执行最后的否则分支，然后退出整个多分支结构。

注意上面流程图的执行特点：对于流程图中的任意一个“不成立”，如果能执行到这里，意味着前面所有的条件都不成立；对于最后一个“不成立”，如果能执行到这里，意味着所有的条件都不成立。

对应的是if...else if...else结构，这里else if可以有多个：

#include<iostream>
using namespace std;
int main()
{
	if(条件1){
		//条件1成立时执行的语句

	}else if(条件2){
		//条件1不成立、条件2成立时执行的语句

	}else if(条件3){
		//条件1不成立、条件2不成立、条件3成立时执行的语句
			
	}...else if(条件n){
		//前面条件都不成立、条件n成立时执行的语句

	}else{
		//前面条件都不成立时执行的语句

	} 
	return 0;
}

再通过一个例子来巩固if...else if...这样的if嵌套结构和该语句体现的算法策略（每次从剩余情况中分出一种）：

已知分段函数（自变量$x$位于不同的取值范围，$y$对于$x$的函数不同）如下，输入$x$，计算并输出$y$：

$$ y=\left\{ \begin{aligned} x^3+2x^2+1\ (x \ge 10) \\ x+1\ (5 \le x <10) \\ 0\ (-5 < x <5)\\ -x-1\ (-10 < x \le -5)\\-x^3-2x^2-1\ (x \le -10)\end{aligned} \right. $$

分段函数一共5段，每次分出一种情况（一段）来处理：

如果x>=10，那么...
否则如果x>=5，那么...
否则如果x>-5，那么...
否则如果x>-10，那么...
否则，...

#include<cstdio>
int main()
{
	double x,y;
	scanf("%lf",&x);
	if(x>=10) y = x*x*x+2*x*x+1;
	else if(x>=5) y = x+1;
	else if(x>-5) y = 0;
	else if(x>-10) y = -x-1;
	else y = -x*x*x-2*x*x-1;
	printf("%.5lf",y);
	return 0;
}

注意使用if...else if...时要同时联想到它的流程图，大家体会上面程序else if的条件为什么可以简写，例如第一个else if，条件不用写成 x>=5 && x<10，直接用x>=5即可。

二、“打擂”求极值

还是上面求三个整数最大值的问题，还可以这样分类讨论：

如果a>b，那么b肯定不是最大值，不用考虑b，但需要考虑a、c的大小关系，可以再分两种情况讨论：
1. a>c：最大值是a
2. 其它情况（a<=c）：最大值是c
其它情况（a<=b），那么a肯定不是最大值，不用考虑a，但需要考虑b、c的大小关系，可以再分两种情况讨论：
1. b>c：最大值是b
2. 其它情况（b<=c）：最大值是c

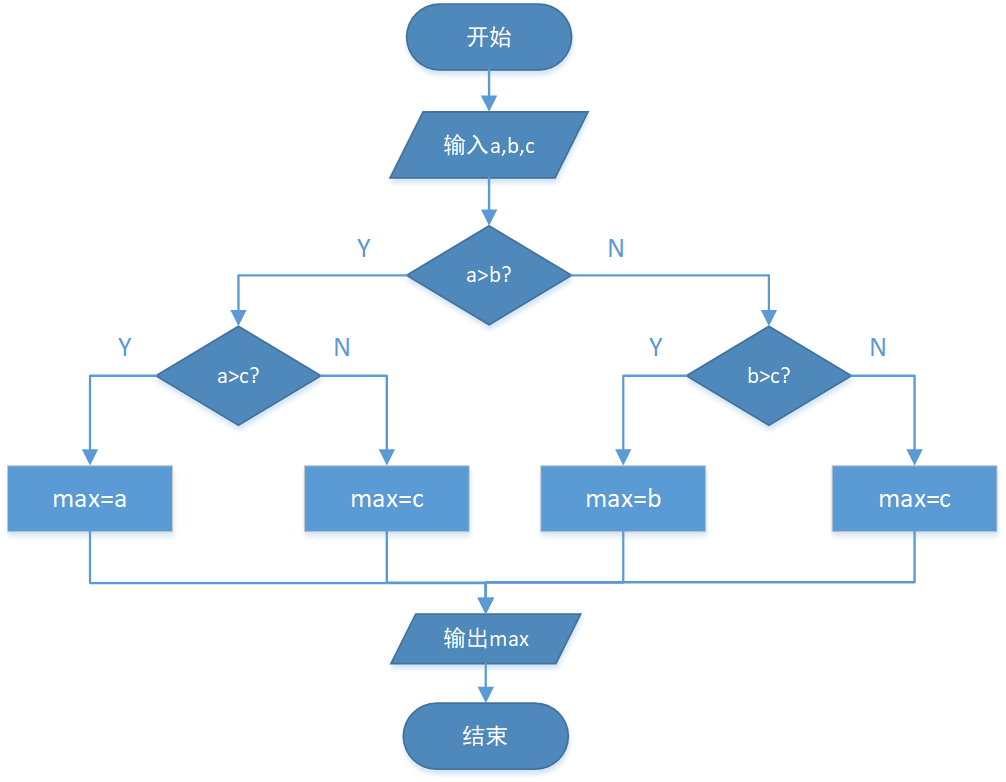
从流程图可以明显看出来，if语句的if子句部分和else子句部分都嵌套了if语句：

#include<iostream>
using namespace std;
int main()
{
	int a,b,c,max;
	cin>>a>>b>>c; 
	if(a>b){      //a>b，那么此时只需要考虑a、c 
		if(a>c) max = a;
		else max = c;
	}else{		//a<=b(else)，那么此时只需要考虑b、c
		if(b>c) max = b;
		else max = c;
	}
	cout<<max<<endl;
	return 0;
}

这里强调代码缩进对于确保程序可读性的重要性，我们对比下面两段代码就能体会到：

#include<iostream>
using namespace std;
int main()
{
	int a,b,c,max;
	cin>>a>>b>>c; 
	if(a>b){
		if(a>c)
			max = a;
		else
			max = c;
	}else{
		if(b>c)
			max = b;
		else
			max = c;
	}
	cout<<max<<endl;
	return 0;
}

#include<iostream>
using namespace std;
int main()
{
int a,b,c,max;
cin>>a>>b>>c; 
if(a>b){
if(a>c)
max = a;
else
max = c;
}else{
if(b>c)
max = b;
else
max = c;
}
cout<<max<<endl;
return 0;
}

大家在编程时，特别是初学阶段，一定要注意良好编码习惯的养成！

还可以模拟现实生活中“打擂台”的方式来求最大值：

用一个变量$max$记录最大值，首先第一个数$a$站到擂台上，那么此时最大值就是$a$（$max=a$），接下来每次都是一个新数字上到擂台上，和擂台上的留下的数字$max$比较大小（两两“打擂”），哪一个数字大就留到擂台上（其实就是更新变量$max$的值），那么所有的数都处理结束后，最大值就保存在变量$max$中（其实每处理完一个数，已经处理过的所有数的最大值就是变量$max$）。

假设$a=1,b=3,c=2$

处理整数$a$，$max$直接赋值成$a$。处理后$max$的值是1；
处理整数$b$，$max$值赋值成$max$（1）和$b$（3）的最大值。处理后$max$的值是3，此时$max$是$a,b$的最大值；
处理整数$c$，$max$值赋值成$max$（3）和$c$（2）的最大值。处理后$max$的值仍然是3，此时$max$是$a,b,c$的最大值。

#include<iostream>
using namespace std;
int main()
{
    int a,b,c,max;
    cin>>a>>b>>c; 

    max = a;
    
    if(b>max) max = b;
    
    if(c>max) max = c;
    
    cout<<max<<endl;
    return 0;
}

在上面程序的基础上，添加相似代码很容易实现求更多整数的最大值。

如果我们再添加一个前提条件：三个整数都是正整数，我们还可以进一步修改代码，让代码更加工整：

#include<iostream>
using namespace std;
int main()
{
	//求三个正整数a、b、c的最大值（注意：a、b、c都是正整数） 
    int a,b,c,max;
    cin>>a>>b>>c; 

    max = 0;   //体会这里赋值成0的用途 
    
    if(a>max) max = a;
    
    if(b>max) max = b;
    
    if(c>max) max = c;
    
    cout<<max<<endl;
    return 0;
}

再来分析前面的代码，程序结构有if嵌套结构，还有先后执行的多个if语句：

#include<iostream>
using namespace std;
int main()
{
    int a,b,c,max;
    cin>>a>>b>>c; 
    if(a>b&&a>c){
        max = a;
    }else if(b>a && b>c){
        max = b;
    }else{
        max = c;
    }
    cout<<max<<endl;
    return 0;
}

#include<iostream>
using namespace std;
int main()
{
    int a,b,c,max;
    cin>>a>>b>>c; 

    max = a;
    
    if(b>max) max = b;
    
    if(c>max) max = c;
    
    cout<<max<<endl;
    return 0;
}

最后来探讨一下程序的效率问题。仍然是计算三个整数最大值，前面说过可以分三种情况讨论（这里的描述和前面稍微不同）：

a>=b && a>=c，此时最大值是a；
b>=a && b>=c，此时最大值是b；
c>=a && c>=b，此时最大值是c。

不少同学自然地使用了先后三个if语句来实现：

#include<iostream>
using namespace std;
int main()
{
    int a,b,c,max;
    cin>>a>>b>>c; 
    if(a>=b && a>=c){
        max = a;
    }
	if(b>=a && b>=c){
        max = b;
    }
	if(c>=a && c>=b){
        max = c;
    }
    cout<<max<<endl;
    return 0;
}

对比前面使用if...else if...语句实现方式：

#include<iostream>
using namespace std;
int main()
{
    int a,b,c,max;
    cin>>a>>b>>c; 
    if(a>b && a>c){
        max = a;
    }else if(b>a && b>c){
        max = b;
    }else{
        max = c;
    }
    cout<<max<<endl;
    return 0;
}

上面两段程序均能很好地解决问题，但是分析执行流程会发现第2段程序执行效率更高：第1段程序，不管a,b,c大小如何，都要经过3次判断处理；第2段程序，如果a最大，那么只需要判断1次，并且不管a,b,c大小如何最多只判断2次。

分类讨论时，如果用多个先后的if语句实现，要特别注意一般要保证有一个并且只有一个if语句条件成立。还是以求三个整数的最大值为例，下面的程序当三个整数值相同时，就不能保证这一点，要么程序没有输出，要么程序输出多次：

#include<iostream>
using namespace std;
int main()
{
    //试试输入三个相同的整数，程序不会有输出
    int a,b,c;
    cin>>a>>b>>c; 
    if(a>b && a>c) cout<<a<<endl; 
    if(b>a && b>c) cout<<b<<endl; 
    if(c>a && c>b) cout<<c<<endl; 
    return 0;
}

#include<iostream>
using namespace std;
int main()
{
    //试试输入三个相同的整数，程序会输出三次
    int a,b,c;
    cin>>a>>b>>c; 
    if(a>=b && a>=c) cout<<a<<endl; 
    if(b>=a && b>=c) cout<<b<<endl; 
    if(c>=a && c>=b) cout<<c<<endl; 
    return 0;
}

一	二	三	四	五	六	日
		1	2	3	4	5
6	7	8	9	10	11	12
13	14	15	16	17	18	19
20	21	22	23	24	25	26
27	28	29	30	31

一、if语句的嵌套与多分支结构

二、“打擂”求极值

其他操作