一、除法结果
【问题描述】
输入两个整数\(a,b\),按如下三种情况计算 \(a \div b\) 的结果:
- 如果\(b =0\),输出
Error; - 如果\(a\)能被\(b\)整除,输出除法的商;
- 如果\(a\)不能被\(b\)整除,输出除法的结果,保留2位小数。
其实题目描述已经很清晰了,分三种情况处理,可以很容易写出if...else if...else的多重分支结构:
#include<iostream>
#include<iomanip>
using namespace std;
int main()
{
int a,b;
cin>>a>>b;
if(b==0) cout<<"Error"<<endl;
else if(a%b==0) cout<<a/b<<endl;
else cout<<fixed<<setprecision(2)<<1.0*a/b<<endl;
return 0;
}
此外,这里介绍一种“特判”的编程思路,特判就是特殊判断处理,也就是把某个或者一些特殊的情况(使用if语句)优先处理。例如本题中的除数为0的情况就可以用特判优先处理:
#include<iostream>
#include<iomanip>
using namespace std;
int main()
{
int a,b;
cin>>a>>b;
if(b==0) { //特判
cout<<"Error"<<endl;
return 0; //注意:这里的return 0;会强制结束程序
}
//有了前面的特判,接下来就不用再考虑b==0的情况了
if(a%b==0) cout<<a/b<<endl;
else cout<<fixed<<setprecision(2)<<1.0*a/b<<endl;
return 0;
}
注意体会这里介绍的“特判”的解题思路。上面的例子还不能很好地体现出“特判”解题的优势。当某些特殊情况很容易得出结果,其它情况需要较复杂处理的时候,使用特判将特殊情况优先处理,然后就可以集中精力处理其它情况。
二、[洛谷]P1425 小鱼的游泳时间
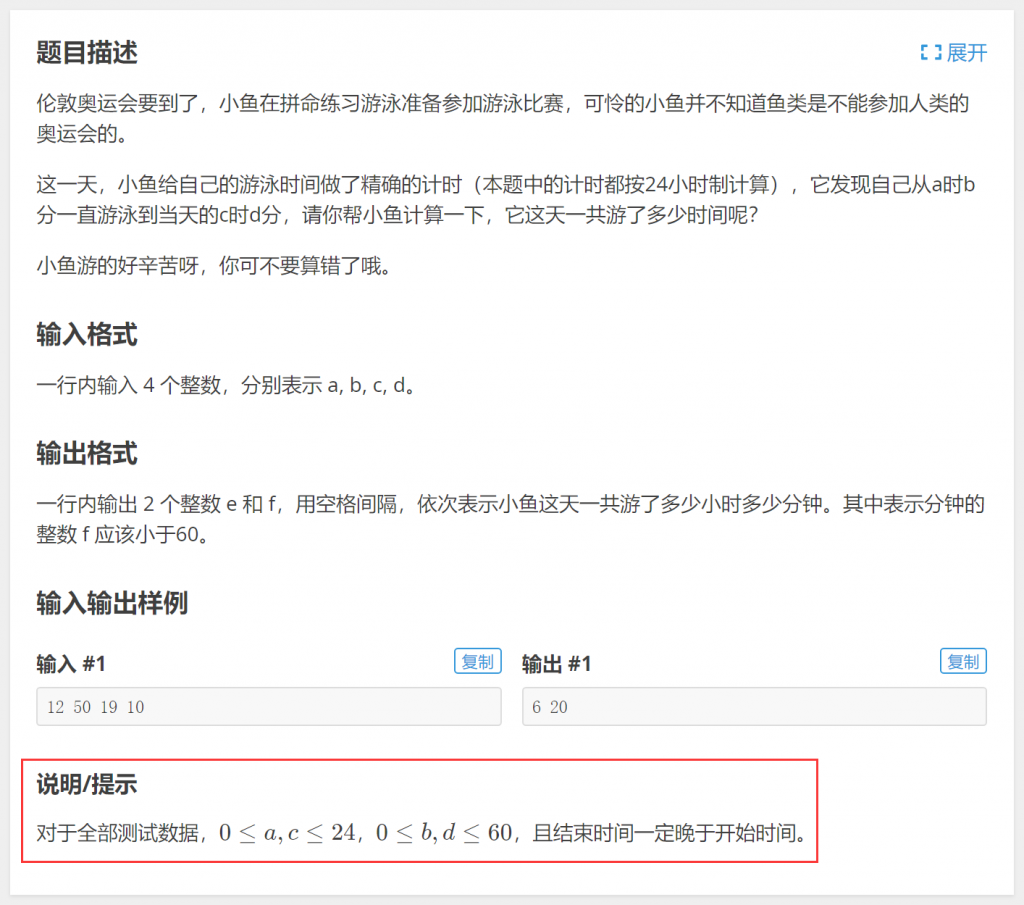
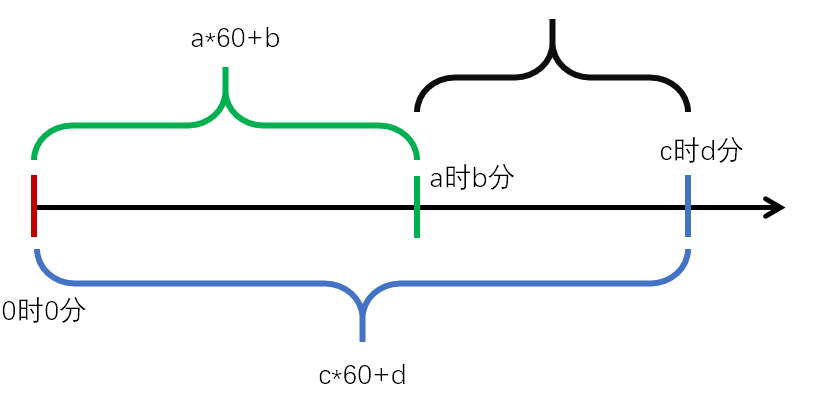
顺序结构例题中已经做过讲解,再来回顾一下顺序结构处理方法:
#include<iostream>
using namespace std;
int main()
{
int a,b,c,d,t;
cin>>a>>b>>c>>d;
t = (c*60+d)-(a*60+b);
cout<<t/60<<" "<<t%60;
return 0;
}
这里不能直接输出\(c-a\)作为小时数,\(d-b\)作为分钟数,因为有可能\(d<b\)。其实可以将这样的情况用if语句特殊处理:
#include<iostream>
using namespace std;
int main()
{
int a,b,c,d,h,m;
cin>>a>>b>>c>>d;
h = c-a;
m = d-b;
if(m<0){ //分钟数为负数
h--; //小时数-1
m += 60; //借1当60,分钟数+60
}
cout<<h<<" "<<m;
return 0;
}
三、小规模排序
1.两个整数升序排序
问题描述:输入两个整数\(a,b\),按照从小到大的顺序输出这两个数。
思路一:如果\(a<b\),那么依次输出\(a,b\),否则依次输出\(b,a\)
#include<iostream>
using namespace std;
int main()
{
int a,b;
cin>>a>>b;
if(a<b) cout<<a<<" "<<b<<endl;
else cout<<b<<" "<<a<<endl;
return 0;
}
思路二:程序最后依次输出\(a,b\)。如果\(a \le b\),此时依次输出\(a,b\)正好是升序排序结果。如果\(a>b\),在依次输出\(a,b\)前可以交换\(a,b\)的值(题目要求是升序,\(a>b\)此时\(a,b\)与要求顺序不符合,那么交换两者的值)。
#include<iostream>
using namespace std;
int main()
{
int a,b,t;
cin>>a>>b;
if(a>b){
t = a;
a = b;
b = t;
}
cout<<a<<" "<<b<<endl;
return 0;
}
2.三个整数升序排序
问题描述:输入三个整数\(a,b,c\),按照从小到大的顺序输出这三个数。同上一个问题比较,问题规模稍微加大。
思路一:分六种情况讨论,使用if...else if...实现:
- 如果a<=b && b<=c,那么输出a,b,c;
- 否则如果a<=c && c<=b,那么输出a,c,b;
- 否则如果b<=a && a<=c,那么输出b,a,c;
- 否则如果b<=c && c<=a,那么输出b,c,a;
- 否则如果c<=a && a<=b,那么输出c,a,b;
- 否则(也就是c<=b && b<=a),输出c,b,a;
#include<iostream>
using namespace std;
int main()
{
int a,b,c;
cin>>a>>b>>c;
if(a<=b && b<=c) cout<<a<<" "<<b<<" "<<c<<endl;
else if(a<=c && c<=b) cout<<a<<" "<<c<<" "<<b<<endl;
else if(b<=a && a<=c) cout<<b<<" "<<a<<" "<<c<<endl;
else if(b<=c && c<=a) cout<<b<<" "<<c<<" "<<a<<endl;
else if(c<=a && a<=b) cout<<c<<" "<<a<<" "<<b<<endl;
else cout<<c<<" "<<b<<" "<<a<<endl;
return 0;
}
思路二:仍然使用交换变量的方式来处理。按照下面的步骤依次处理:
- 如果\(a>b\),那么交换\(a,b\)的值(\(a,b\)顺序不对则交换)
- 如果\(a>c\),那么交换\(a,c\)的值(\(a,c\)顺序不对则交换)
经过第1、2步处理后,最小值肯定在变量 \(a\) 中,还需要考虑 \(b,c\) 的顺序是否正确
- 如果\(b>c\),那么交换\(b,c\)的值(\(b,c\)顺序不对则交换)
- 依次输出\(a,b,c\)的值
#include<iostream>
using namespace std;
int main()
{
int a,b,c,t;
cin>>a>>b>>c;
//if语句中如果有多条语句需要使用{},也可以用,将多条语句分隔开,最后用;
//这个时候是一个逗号表达式语句,是一个完整的语句,可以省略{}
if(a>b) t = a,a = b,b = t;
if(a>c) t = a,a = c,c = t;
if(b>c) t = b,b = c,c = t;
cout<<a<<" "<<b<<" "<<c;
return 0;
}
注意:上面的程序注释中介绍了逗号表达式,请仔细阅读!
其实也可以按照下面的步骤来依次处理:
- 如果\(a>b\),那么交换\(a,b\)的值(\(a,b\)顺序不对则交换)
- 如果\(b>c\),那么交换\(b,c\)的值(\(b,c\)顺序不对则交换)
经过第1、2步处理后,最大值肯定在变量 \(c\) 中,还需要考虑 \(a,b\) 的顺序是否正确
- 如果\(a>b\),那么交换\(a,b\)的值(\(a,b\)顺序不对则交换)
- 依次输出\(a,b,c\)的值
四、判断三角形形状
输入三个浮点数\(a,b,c\),判断\(a,b,c\)作为边长能否组成三角形,如果能够组成三角形,判断三角形的形状(等边 or 等腰 or 直角 or 普通)
思路:
1.三条\(a,b,c\)长度的线段能组成三角形的条件:任意两边之和大于第三边,任意两边之差小于第三边。其实只需要判断“任意两边之和大于第三边”即可。注意这里任意的含义,表示随意选出来的两条边的和都要大于第三边,那么条件可以描述为: a+b>c && b+c>a && c+a>b 。
2.判断是否为等边三角形、等腰三角形:等边三角形的条件很容易想到 a==b && b==c。等腰三角形的腰可以是\(a,b\),也可以是\(b,c\),也可以是\(c,a\),这三种情况都有可能,那么条件应该描述为:a==b || b==c || c==a。再来考虑判断顺序,对于等边三角形和等腰三角形,应该先判断等边再判断等腰(思考原因)。
3.判断直角三角形:和判断等腰三角形相似,\(a,b,c\)都有可能是斜边,所以条件可以描述为:a*a+b*b==c*c || b*b+c*c==a*a || c*c+a*a==b*b。
#include<iostream>
using namespace std;
int main()
{
double a,b,c;
cin>>a>>b>>c;
if(a>0 && b>0 && c>0 && a+b>c && b+c>a && c+a>b){
//判断顺序:
//等边->直角(等腰直角 or 普通直角)->等腰->普通
//思考:这个判断顺序可以随意改变吗?
if(a==b && b==c){
cout<<"等边三角形";
}else if(a*a+b*b==c*c || b*b+c*c==a*a || c*c+a*a==b*b){
if(a==b || b==c || c==a){ //几乎不可能找到测试样例满足等腰直角三角形
cout<<"等腰直角三角形";
}else{
cout<<"普通直角三角形";
}
}else if(a==b || b==c || c==a){
cout<<"等腰三角形";
}else{
cout<<"普通三角形";
}
}else{
cout<<"不能组成三角形";
}
return 0;
}
五、小组成员成绩分析
小组有4位成员,参加了测试,测试总分为100分,60分及以上为及格,85分及以上为优秀。现在提供4位小组成员的成绩\(a,b,c,d\),判断下面的情况是否成立:
- 恰好只有1位成员不及格
- 不及格人数不超过3人
- 及格人数不少于3人,优秀人数不少于2人
- 不及格人数和优秀人数的和不超过2人
思路一:借助复合逻辑运算列清所有条件
对于情况1,“恰好只有1位成员不及格”,判断的条件可以描述为:(a<60 && b>=60 && c>=60 && d>=60) || (a>=60 && b<60 && c>=60 && d>=60) || (a>=60 && b>=60 && c<60 && d>=60) || (a>=60 && b>=60 && c>=60 && d<60)。
对于情况2,“不及格人数不超过3人”,可以细化为“不及格人数为0”或者“不及格人数为1”或者“不及格人数为2”或者“不及格人数为3”:
- “不及格人数为0”和“全部都及格”是同一个意思,可以描述为:
a>=60 && b>=60 && c>=60 && d>=60; - “不及格人数为1”,可以描述为:
(a<60 && b>=60 && c>=60 && d>=60) || (a>=60 && b<60 && c>=60 && d>=60) || (a>=60 && b>=60 && c<60 && d>=60) || (a>=60 && b>=60 && c>=60 && d<60); - “不及格人数为2”,可以描述为:
(a<60 && b<60 && c>=60 && d>=60) || (a<60 && b>=60 && c<60 && d>=60) || (a<60 && b>=60 && c>=60 && d<60) || (a>=60 && b<60 && c<60 && d>=60) || (a>=60 && b<60 && c>=60 && d<60) || (a>=60 && b>=60 && c<60 && d<60); - “不及格人数为3”和“恰好只有1个人及格”是同一个意思,可以描述为:
(a>=60 && b<60 && c<60 && d<60) || (a<60 && b>=60 && c<60 && d<60) || (a<60 && b<60 && c>=60 && d<60) || (a<60 && b<60 && c<60 && d>=60)。
经过上面分析,“不及格人数不超过3人”的完整条件可以描述为:(a>=60 && b>=60 && c>=60 && d>=60) || ((a<60 && b>=60 && c>=60 && d>=60) || (a>=60 && b<60 && c>=60 && d>=60) || (a>=60 && b>=60 && c<60 && d>=60) || (a>=60 && b>=60 && c>=60 && d<60)) || ((a<60 && b<60 && c>=60 && d>=60) || (a<60 && b>=60 && c<60 && d>=60) || (a<60 && b>=60 && c>=60 && d<60) || (a>=60 && b<60 && c<60 && d>=60) || (a>=60 && b<60 && c>=60 && d<60) || (a>=60 && b>=60 && c<60 && d<60)) || ((a>=60 && b<60 && c<60 && d<60) || (a<60 && b>=60 && c<60 && d<60) || (a<60 && b<60 && c>=60 && d<60) || (a<60 && b<60 && c<60 && d>=60))。要完全理清、读懂,表示压力很大!为了增强可读性,可以这样来编写程序:
bool b1 = a>=60 && b>=60 && c>=60 && d>=60;
bool b2 = (a<60 && b>=60 && c>=60 && d>=60) || (a>=60 && b<60 && c>=60 && d>=60) || (a>=60 && b>=60 && c<60 && d>=60) || (a>=60 && b>=60 && c>=60 && d<60);
bool b3 = (a<60 && b<60 && c>=60 && d>=60) || (a<60 && b>=60 && c<60 && d>=60) || (a<60 && b>=60 && c>=60 && d<60) || (a>=60 && b<60 && c<60 && d>=60) || (a>=60 && b<60 && c>=60 && d<60) || (a>=60 && b>=60 && c<60 && d<60);
bool b4 = (a>=60 && b<60 && c<60 && d<60) || (a<60 && b>=60 && c<60 && d<60) || (a<60 && b<60 && c>=60 && d<60) || (a<60 && b<60 && c<60 && d>=60);
if(b1 || b2 || b3 || b4){
}
对于情况3,使用“复合逻辑运算列清所有条件”这样的思路,表示压力很大!
对于情况4,感觉无从下手,其实“不及格人数和优秀人数的和不超过2人”和“成绩不低于60分并且小于85分的人数不低于2人”是同一个意思,不过使用“复合逻辑运算列清所有条件”处理起来仍然很繁琐!
思路二:其实现实生活中我们的处理上面问题的方法是非常朴素的——数数。编程时可以直接模拟现实生活中的数数,使用“计数器”来统计及格(或者不及格)的人数即可。算法有一个重要的来源就是模拟现实生活中处理问题的方法。
对于情况1,参考代码如下:
#include<iostream>
using namespace std;
int main()
{
int a,b,c,d,tot=0;
cin>>a>>b>>c>>d;
if(a<60) tot++;
if(b<60) tot++;
if(c<60) tot++;
if(d<60) tot++;
if(tot==1){
cout<<"恰好只有一人不及格";
}
return 0;
}
对于情况2,参考代码如下:
#include<iostream>
using namespace std;
int main()
{
int a,b,c,d,tot=0;
cin>>a>>b>>c>>d;
if(a<60) tot++;
if(b<60) tot++;
if(c<60) tot++;
if(d<60) tot++;
if(tot<=3){
cout<<"不及格人数不超过3人";
}
return 0;
}
对于情况3,参考代码如下:
#include<iostream>
using namespace std;
int main()
{
int a,b,c,d,tot1=0,tot2=0; //tot1不及格人数,tot2优秀人数
cin>>a>>b>>c>>d;
if(a<60) tot1++;
else if(a>=85) tot2++;
if(b<60) tot1++;
else if(b>=85) tot2++;
if(c<60) tot1++;
else if(c>=85) tot2++;
if(d<60) tot1++;
else if(d>=85) tot2++;
if(tot1>=3 && tot2>=2){
cout<<"及格人数不少于3人,优秀人数不少于2人";
}
return 0;
}
对于情况4,我们可以自行在情况3的基础上修改代码解决问题。
 NOIP学习小站
NOIP学习小站