正如选择结构if语句的if子句和else子句可以嵌套if语句一样,循环语句的循环体中也能出现循环语句,这就是循环的嵌套,也称为多重循环。就以钟表的分针和秒针为例,分针每走一格,秒针都要走完整一圈。分针走动多格可以用循环来描述,这是“大操作”,“大操作”的每一步(分针走一格)都是重复的小操作(秒针走一格重复60次实现的分针走一圈效果),这就是典型的循环嵌套(双重循环)。如果再考虑上时针,那么就是三重循环。
一、结构化程序设计
我们解决的问题会越来越复杂,写出的程序结构同样如此。随着我们对算法和程序设计越来越熟悉,分析问题、理清思路后,往往会预先结合程序的框架来描述设计的算法,这里体现的是结构化程序设计的思想。
结构化程序设计(structured programming)是进行以模块功能和处理过程设计为主的详细设计的基本原则。结构化程序设计采用自顶向下、逐步求精的设计方法,各个模块通过“顺序、选择、循环”的控制结构进行连接,并且只有一个入口、一个出口。
以前面的累加求和(\(1+2+3+...+n\))为例,结构化程序设计首先是自顶向下搭建以功能模块为基本单位的框架:
- 输入n
- 利用循环结构和累加器求和
- 输出结果
然后再逐步求精,细化各个功能模块,完善整个程序:
#include<iostream>
using namespace std;
int main()
{
int n,s=0;
cin>>n;
for(int i=1;i<=n;i++){
s += i;
}
cout<<s;
return 0;
}
只要我们分析设计出程序的框架(描述出要实现的各个功能模块),接下来要做的就是将框架中的各个功能模块逐步细化实现。在循环结构特别是循环嵌套的时候,往往要用循环的控制变量来抽象化地描述程序的框架。这里通过几个经典的问题,在说明循环嵌套如何使用的同时,阐述如何用循环的控制变量来抽象化地描述程序的框架的解题思想。
二、双重循环实现图形打印
首先来看一个简单的问题,输出3行2列由字符'*'拼成的矩形,效果如下:
** ** **
一共要输出3行,可以用一个重复执行3次的循环实现,并且每行输出的内容都相同cout<<"**"<<endl;,初步实现的代码如右侧所示:
#include<iostream>
using namespace std;
int main()
{
//重复3次,一共输出3行
for(int i=1;i<=3;i++){
//每次都输出"**"并换行
cout<<"**"<<endl;
}
return 0;
}
考虑到循环体中的cout<<"**"<<endl;语句,其实也可以用一个重复执行2次,每次输出一个"*"的循环语句来实现,可以将程序如下修改:
#include<iostream>
using namespace std;
int main()
{
//重复3次,一共输出3行
for(int i=1;i<=3;i++){
//每行都输出2个"*"
for(int j=1;j<=2;j++){
cout<<"*";
}
//再换行
cout<<endl;
}
return 0;
}
仔细观察程序的结构,会发现for循环的循环体中又出现了for循环,这就是循环的嵌套,这里是双重循环。外层控制输出3行的for循环称为外层循环,内层控制每行输出2个*的for循环称为内层循环。
在循环嵌套结构中,内层循环控制变量一般与外层循环不同,否则可能会干扰外层循环的执行流程。
关于字符图形打印可以得出结论:外层循环控制图形行数,内层循环控制每行打印的内容(每行字符个数)。
我们先从细节入手来分析双重循环的执行流程,帮助我们进一步熟悉掌握循环结构的执行流程。我们现在应该得具备将流程图和程序互相转换的能力,也就是看到三大结构的程序,我们能够很快想到执行流程图;有了流程图,我们能够快速写出对应的三大结构程序代码。
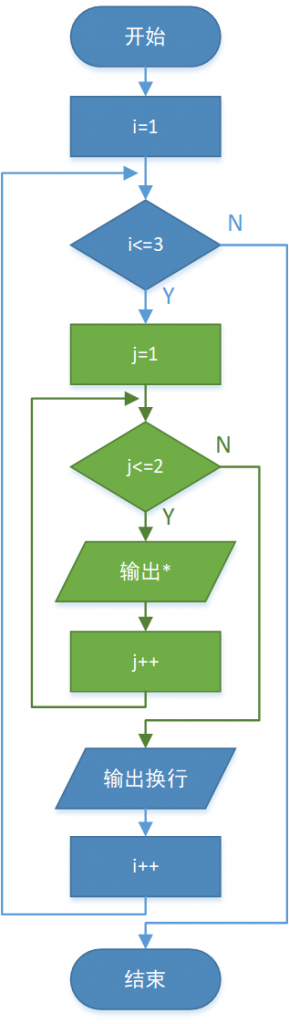
图中绿色部分是内层循环,我们仍然可以借助表格来追踪控制变量值的变化情况来分析执行细节:
| i值 | i<=3? | j值 | j<=2? | 执行循环体 | 循环结束后 |
| 1 | Y | 进入内层循环 | |||
| 1 | Y | 输出* | j++,j为2 | ||
| 2 | Y | 输出* | j++,j为3 | ||
| 3 | N | 退出内层循环 | |||
| 输出换行 | i++,i为2 | ||||
| 2 | Y | 进入内层循环 | |||
| 1 | Y | 输出* | j++,j为2 | ||
| 2 | Y | 输出* | j++,j为3 | ||
| 3 | N | 退出内层循环 | |||
| 输出换行 | i++,i为3 | ||||
| 3 | Y | 进入内层循环 | |||
| 1 | Y | 输出* | j++,j为2 | ||
| 2 | Y | 输出* | j++,j为3 | ||
| 3 | N | 退出内层循环 | |||
| 输出换行 | i++,i为4 | ||||
| 4 | N | 退出外层循环 |
再从结构化程序设计的思想来分析程序,相比较前面的借助表格微观分析执行流程的细节,这里就是宏观描述程序的框架,程序的框架如下:
//重复3次,一共输出3行
for(int i=1;i<=3;i++){
//输出2个"*"
//换行
}
编写复杂程序时,我们往往通过算法最先联想到的是程序的框架,甚至先书写框架再逐步细化实现每个模块功能。
再来看复杂点的字符图形输出,要输出如下边长为5的等腰直角字符三角形:
* ** *** **** *****
容易想到,这里仍然可以使用双重循环实现,外层循环控制行数,所以外层循环可以用一个重复执行5次的for循环。内层循环控制每行打印的字符数量,但是每行的字符数量不同,但存在一定的规律。
| 行编号 | 行内字符数量 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
通过左边表格分析寻找规律,可知行内打印字符的数量和行编号一致,可以更为抽象地描述为:第i行输出i个字符。那么程序的框架可以描述为:
//重复5次,一共输出5行
for(int i=1;i<=5;i++){
//循环体内语句的功能可以描述为:输出第i行的内容
//第①步:输出i个"*"
//第②步:换行
}
注意体会并学会这样的抽象描述循环体功能并进一步描述整个程序框架的方法。往往会借助循环的控制变量来抽象描述,就像这里的“循环体的功能是输出第i行的内容”、“第①步是要输出i个*”。有了这样描述的程序框架,完整的程序就能很容易写出来了:
#include<iostream>
using namespace std;
int main()
{
//重复5次,一共输出5行
for(int i=1;i<=5;i++){
//输出i个"*"(循环体只有一句代码,省略了{}并写到了一行中)
for(int j=1;j<=i;j++) cout<<"*";
//换行
cout<<endl;
}
return 0;
}
再来看一个更复杂的字符图形输出,要输出如下边长为5的直角在右下角的等腰直角字符三角形:
* ** *** **** *****
通过分析可知,仍然是5行,仍然是第i行i个*,不过内容“居右对齐”了,其实可以通过在输出i个*之前输出若干个空格将*挤到右侧。还是来分析寻找每行空格数和字符数的规律:
| 行编号 | 行内空格数 | 行内字符数量 |
| 1 | 4 | 1 |
| 2 | 3 | 2 |
| 3 | 2 | 3 |
| 4 | 1 | 4 |
| 5 | 0 | 5 |
通过左边表格分析寻找规律,可知第i行先输出5-i个空格,再输出i个字符。那么程序的框架可以描述为:
//重复5次,一共输出5行
for(int i=1;i<=5;i++){
//循环体内语句的功能可以描述为:输出第i行的内容
//第①步:输出5-i个" "
//第②步:输出i个"*"
//第③步:换行
}
有了程序框架,完整的程序很容易写出来:
#include<iostream>
using namespace std;
int main()
{
//重复5次,一共输出5行
for(int i=1;i<=5;i++){
//输出5-i个" "
for(int j=1;j<=5-i;j++){
cout<<" ";
}
//输出i个"*"
for(int k=1;k<=i;k++){
cout<<"*";
}
//换行
cout<<endl;
}
return 0;
}
#include<iostream>
using namespace std;
int main()
{
//重复5次,一共输出5行
for(int i=1;i<=5;i++){
//输出5-i个" "
for(int j=1;j<=5-i;j++){
cout<<" ";
}
//控制变量仍然可以用j
for(int j=1;j<=i;j++){
cout<<"*";
}
//换行
cout<<endl;
}
return 0;
}
会发现我们现在写的程序结构越来越复杂,上面程序循环体中出现了先后顺序的循环。注意第二段程序,即使是将控制变量放在main开始处定义,外层循环体的第二个循环仍然可以用第一个循环相同的控制变量:
#include<iostream>
using namespace std;
int main()
{
int i,j; //循环控制变量在循环前定义
for(i=1;i<=5;i++){
for(j=1;j<=5-i;j++) cout<<" ";
//上面循环结束后,j的值已经没有任何作用了,所以后面的循环仍然用j作为控制变量
//并且for循环开始前会执行控制变量赋初值,
//所以上一个循环结束后的j值会被覆盖,不会影响到后面的循环
for(j=1;j<=i;j++) cout<<"*";
cout<<endl;
}
return 0;
}
习题:尝试使用双重循环打印以下字符图形:
***** **** *** ** *
*****
****
***
**
*
* *** ***** ******* *********
*********
*******
*****
***
*
三、打印九九乘法表
问题:打印如下九九乘法表
1*1=1 1*2=2 2*2=4 1*3=3 2*3=6 3*3=9 1*4=4 2*4=8 3*4=12 4*4=16 1*5=5 2*5=10 3*5=15 4*5=20 5*5=25 1*6=6 2*6=12 3*6=18 4*6=24 5*6=30 6*6=36 1*7=7 2*7=14 3*7=21 4*7=28 5*7=35 6*7=42 7*7=49 1*8=8 2*8=16 3*8=24 4*8=32 5*8=40 6*8=48 7*8=56 8*8=64 1*9=9 2*9=18 3*9=27 4*9=36 5*9=45 6*9=54 7*9=63 8*9=72 9*9=81
分析:其实和前面打印字符三角形一样,这里一共要打印9行,第 \(i\) 行有 \(i\) 个算式,每个算式都是cout<<A<<"*"<<B<<"="<<A*B;这样的形式(可以猜想到A、B可能和循环的控制变量相关),得出程序的框架:
#include<iostream>
using namespace std;
int main()
{
for(int i=1;i<=9;i++){
for(int j=1;j<=i;j++){
//输出第i行第j个算式,形式是cout<<A<<"*"<<B<<"="<<A*B;
}
cout<<endl;
}
return 0;
}
接下来,通过找规律来抽象归纳cout<<A<<"*"<<B<<"="<<A*B;中A、B究竟是什么?
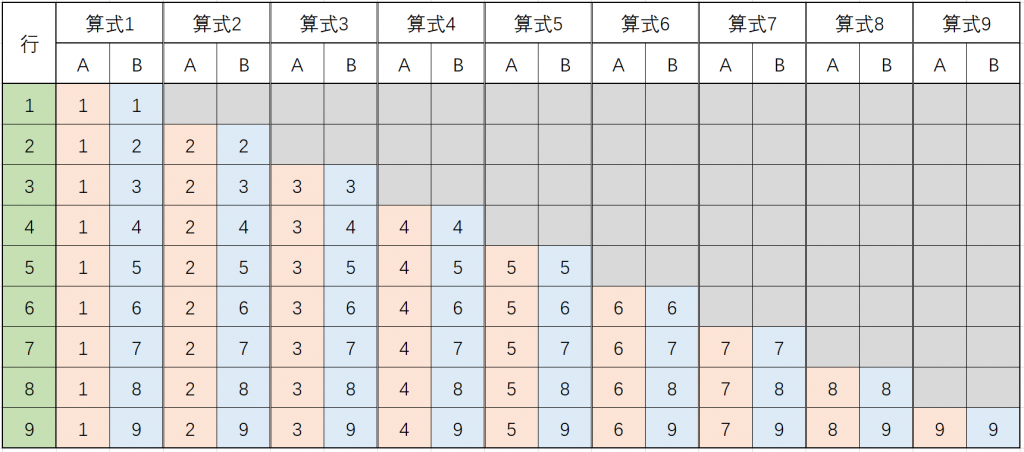
先来看B,以第6行为例:

1*6=6 2*6=12 3*6=18 4*6=24 5*6=30 6*6=36
我们会发现第 \(i\) 行的每个算式乘号*右边的数B就是外层循环控制变量 \(i\) 。
再来看A,仍然以第6行为例:

1*6=6 2*6=12 3*6=18 4*6=24 5*6=30 6*6=36
第1个算式的A是1,第2个算式的A是2,……,可知行内第 \(j\) 个算式乘号*左边的数A正好是内层循环控制变量 \(j\)。
那么输出的算式应该是:cout<<j<<"*"<<i<<"="<<j*i;,进一步考虑结果是1位数和2位数的不同处理,完整的程序代码如下:
#include<iostream>
using namespace std;
int main()
{
for(int i=1;i<=9;i++){
for(int j=1;j<=i;j++){
cout<<j<<"*"<<i<<"="<<j*i<<" ";
if(j*i<10) cout<<" ";
}
cout<<endl;
}
return 0;
}
习题:尝试打印下面风格的九九乘法表
1*1=1 2*1=2 2*2=4 3*1=3 3*2=6 3*3=9 4*1=4 4*2=8 4*3=12 4*4=16 5*1=5 5*2=10 5*3=15 5*4=20 5*5=25 6*1=6 6*2=12 6*3=18 6*4=24 6*5=30 6*6=36 7*1=7 7*2=14 7*3=21 7*4=28 7*5=35 7*6=42 7*7=49 8*1=8 8*2=16 8*3=24 8*4=32 8*5=40 8*6=48 8*7=56 8*8=64 9*1=9 9*2=18 9*3=27 9*4=36 9*5=45 9*6=54 9*7=63 9*8=72 9*9=81
1*1=01
1*2=02 2*2=04
1*3=03 2*3=06 3*3=09
1*4=04 2*4=08 3*4=12 4*4=16
1*5=05 2*5=10 3*5=15 4*5=20 5*5=25
1*6=06 2*6=12 3*6=18 4*6=24 5*6=30 6*6=36
1*7=07 2*7=14 3*7=21 4*7=28 5*7=35 6*7=42 7*7=49
1*8=08 2*8=16 3*8=24 4*8=32 5*8=40 6*8=48 7*8=56 8*8=64
1*9=09 2*9=18 3*9=27 4*9=36 5*9=45 6*9=54 7*9=63 8*9=72 9*9=81
三、百钱买百鸡
问题:公鸡5文钱一只,母鸡3文钱一只,小鸡1文钱三只,用100文钱买100只鸡(每种鸡都得有)。如何购买?

我国古代数学家张丘建在《算经》一书中曾提出过著名的“百钱买百鸡”问题,该问题叙述如下:鸡翁一,值钱五;鸡母一,值钱三;鸡雏三,值钱一;百钱买百鸡,则翁、母、雏各几何?
数学列方程求解,设公鸡数量\(x\)只,母鸡数量\(y\)只,小鸡数量\(z\)只(\(z\)必须是3的倍数),根据题意,可列出方程组:
$$\left\{ \begin{aligned} x+y+z=100 \\ 5x+3y+z/3=100\end{aligned} \right. $$
可知这是一个不定方程,应该有多组解。
分析:来看最简单的暴力求解法,就是一一列举公鸡、母鸡、小鸡数量所有的情况,从中筛选符合条件的组合(下面列举的组合情况只是粗略地考虑):
| 公鸡数量 | 母鸡数量 | 小鸡数量 | 总数 | 钱数 |
| 1 | 1 | 3 | 5 | 3 |
| 1 | 1 | 6 | 8 | 4 |
| 1 | 1 | 9 | 11 | 5 |
| …… | …… | …… | …… | …… |
| 1 | 1 | 300 | 302 | 102 |
| 1 | 2 | 3 | 6 | 4 |
| 1 | 2 | 6 | 9 | 5 |
| …… | …… | …… | …… | …… |
| 1 | 100 | 300 | 401 | 201 |
| 2 | 1 | 3 | 6 | 4 |
| 2 | 1 | 6 | 9 | 5 |
| …… | …… | …… | …… | …… |
| 4 | 18 | 78 | 100 | 100 |
| …… | …… | …… | …… | …… |
| 100 | 1 | 3 | 104 | 102 |
| 100 | 1 | 6 | 107 | 103 |
| …… | …… | …… | …… | …… |
| 100 | 100 | 300 | 500 | 300 |
分析左边的表格,粗略列举了公鸡、母鸡、小鸡数量的组合情况,公鸡数量取值范围1~100,母鸡数量取值范围1~100,小鸡数量取值范围3~300中所有3的倍数(其实三种鸡数量的取值范围都可以再缩小)。
具体组合规则是公鸡1只,母鸡1只,小鸡3~300中所有3的倍数这样有100种组合;然后公鸡1只,母鸡2只,小鸡3~300中所有3的倍数这样也有100种组合……
就像钟表中时针、分针、秒针的走动关系一样,上面的穷举是典型的三重循环:
for(int i=1;i<=100;i++){
for(int j=1;j<=100;j++){
for(int k=3;k<=300;k+=3){
//公鸡i只,母鸡j只,小鸡k只
}
}
}
这就是程序的框架,看到最内层循环中的注释,这里也是抽象地用循环控制变量说明了“公鸡i只,母鸡j只,小鸡k只”。
如果使用前面介绍的用表格来追踪循环的控制变量值变化的情况,会发现和左边的表格中的描述是一致的。
进一步需要判断“公鸡i只,母鸡j只,小鸡k只”是否满足“百钱买百鸡”:
#include<iostream>
using namespace std;
int main()
{
for(int i=1;i<=100;i++){
for(int j=1;j<=100;j++){
for(int k=3;k<=300;k+=3){
//筛选出“百钱买百鸡”的组合
if(i+j+k==100 && 5*i+3*j+k/3==100){
cout<<i<<" "<<j<<" "<<k<<endl;
}
}
}
}
return 0;
}
因为一共要买100只鸡,所以只需要穷举出公鸡和母鸡的组合情况,小鸡的数量可以用减法求出来,这样只需要双重循环就能解决问题。比起前面的三重循环,这样做大大减少了循环次数,提高了程序执行效率:
#include<iostream>
using namespace std;
int main()
{
for(int i=1;i<20;i++){ //公鸡最多买19只(20只公鸡100文)
for(int j=1;j<(100-5*i)/3;j++){ //母鸡数量不超过(100-5*i)/3
//公鸡i只,母鸡j只
int k = 100-i-j; //小鸡数量
//筛选出“小鸡数量必须是3的倍数,并且一共花100文钱”的组合
if(k%3==0 && 5*i+3*j+k/3==100){
cout<<i<<" "<<j<<" "<<k<<endl;
}
}
}
return 0;
}
阅读下面解决百钱买百鸡的程序,理清解决问题的思路:
#include<iostream>
using namespace std;
int main()
{
for(int k=1;k<33;k++){
for(int i=1;i<(100-3*k)/5;i++){
int j=100-3*k-i;
if(k+5*i+3*j==100){
cout<<i<<" "<<j<<" "<<3*k<<endl;
}
}
}
return 0;
}
四、分解质因数
还是来看分解质因数,从\(2\)开始的整数\(i\)判断能否整除\(n\),如果能够整除,那么借助while循环做到一次性“除尽”:
#include<iostream>
using namespace std;
int main()
{
int n,i=2;
cin>>n;
while(n!=1){
//i能整除n,那么一次性“除尽”
while(n%i==0){
cout<<i<<" ";
n /= i;
}
i++;
}
return 0;
}
还可以把外层的while循环改成for循环来精简程序代码:
#include<iostream>
using namespace std;
int main()
{
int n,i=2;
for(cin>>n;n!=1;i++){
//i能整除n,那么一次性“除尽”
while(n%i==0){
cout<<i<<" ";
n /= i;
}
}
return 0;
}
五、强制退出多重循环
通过前面的学习,我们已经知道,在循环体中可以通过break语句强制退出循环。但是在多重循环结构中,break语句只能强制退出当前层级循环,特别是break语句在内层循环体中时,是不能强制退出到外层循环外的。
例如要找到不大于\(n\)的最大合数,下面的程序是有问题的(会输出不大于\(n\)的所有合数):
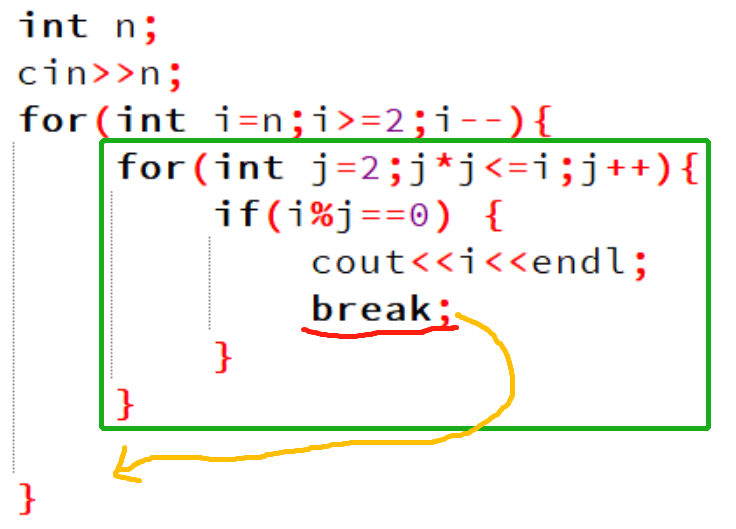
有两种方法来实现效果,第一中方法是使用return 0;语句来强制结束整个程序:
#include<iostream>
using namespace std;
int main()
{
int n;
cin>>n;
for(int i=n;i>=2;i--){
for(int j=2;j*j<=i;j++){
if(i%j==0) {
cout<<i<<endl;
return 0;
}
}
}
return 0;
}
此外还可以使用标记变量的方法来强制退出多重循环:
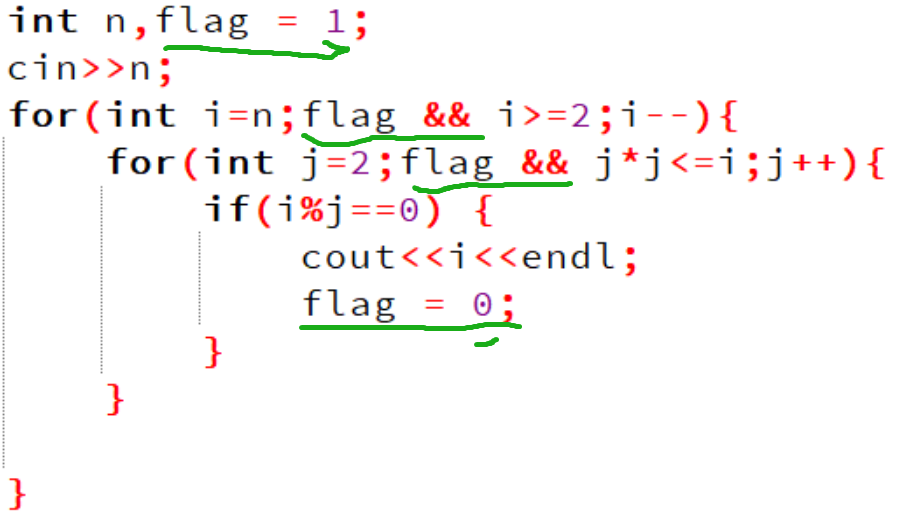
#include<iostream>
using namespace std;
int main()
{
int n,flag = 1;
cin>>n;
for(int i=n;flag && i>=2;i--){
for(int j=2;flag && j*j<=i;j++){
if(i%j==0) {
cout<<i<<endl;
flag = 0;
}
}
}
return 0;
}
注意掌握上面这种方法,特别是在退出循环后还要运行其它程序代码的时候(此时就不能简单地用return 0;语句来强制结束整个程序 )。
 NOIP学习小站
NOIP学习小站