一、阶乘累计求和
问题:已知\(n\)的阶乘: \(n! = 1 \times 2 \times 3 \times ... \times n\)(也就是 \(n! = \prod\limits_{i=1}^{n}i\)),输入正整数\(n\),计算 \(1!+2!+3!+...+n!\)
分析:累计求和需要使用重复n次的循环,循环体内需要嵌套一个循环使用累乘结构计算\(i!\),那么程序的框架可以是:
#include<iostream>
using namespace std;
int main()
{
long long t,s = 0;
int n;
cin>>n;
for(int i=1;i<=n;i++){
// 计算 i!保存到t中(待实现)
s += t;
}
cout<<s;
return 0;
}
进一步实现框架中计算 \(i!\) 的功能模块:
#include<iostream>
using namespace std;
int main()
{
long long t,s = 0;
int n;
cin>>n;
for(int i=1;i<=n;i++){
t = 1;
for(int j=1;j<=i;j++) t *= j;
s += t;
}
cout<<s;
return 0;
}
上面的程序使用了双重循环,可以计算出内层循环语句重复执行的次数(最能体现循环执行效率的指标)是:\(\sum\limits_{i=1}^{n}i = 1+2+3+...+n = \frac{n \times (n+1)}{2}\) 次,其实可以使用简单的循环解决问题:
#include<iostream>
using namespace std;
int main()
{
long long t = 1,s = 0;
int n;
cin>>n;
for(int i=1;i<=n;i++){
t *= i; //t是i!
s += t;
}
cout<<s;
return 0;
}
上面的程序减少了循环的层次,大大减少了循环重复执行的次数(只需要n次),提高了程序运行效率。
二、水仙花数
问题:如果一个三位数每位上的数字的立方和等于这个三位数本身,那么它就是一个“水仙花数”,编程输出所有的“水仙花数”。
思路一:使用循环枚举所有的三位数(100~999),对于每个三位数\(i\),使用数的拆分的方法拆解出个位数、十位上、百位上的数,筛选出每位上的数字的立方和等于\(i\)的数即可。
#include<iostream>
using namespace std;
int main()
{
for(int i=100;i<=999;i++){
int g = i%10;
int s = i/10%10;
int b = i/100%10;
if(g*g*g+s*s*s+b*b*b==i) cout<<i<<" ";
}
return 0;
}
思路二:使用三重循环分别枚举三位数百位、十位、个位上的数字\(b,s,g\),那么三位数\(n\)就是\(b \times 100+s \times 10+g\),筛选出每位上的数字的立方和\(b^3+s^3+g^3\)等于\(n\)的数即可:
#include<iostream>
using namespace std;
int main()
{
for(int b=1;b<=9;b++){
for(int s=0;s<=9;s++){
for(int g=0;g<=9;g++){
//百位上的数b,十位上的数s,个位上的数g
int n = b*100+s*10+g;
if(g*g*g+s*s*s+b*b*b==n) cout<<n<<" ";
}
}
}
return 0;
}
这一种解法虽然是三重循环,但是循环执行的总次数和第一种解法是一致的,甚至效率会稍微高一些(计算机内部乘法运算速度快于除法)。所以不能简单地看循环层次来判断程序的执行效率!
习题:如果一个四位数每位上的数字的四次方和等于这个四位数本身,那么它就是一个“四叶草数”,编程输出所有的“四叶草数”。
三、形如aabb的完全平方数
问题:形如aabb的完全平方数指的是四位数前两位数字相同,后两位数字相同,并且这个四位数是一个完全平方数(开平方结果是整数),编写程序输出所有形如aabb的完全平方数。
思路一:使用双重循环分别枚举高两位的数字\(i\)和低两位的数字\(j\),那么四位数就是\(i \times 1000+i \times 100 + j \times 10 + j\),筛选出其中的完全平方数即可,由此可以得出程序的框架:
#include<iostream>
using namespace std;
int main()
{
for(int i=1;i<=9;i++){ //枚举高两位
for(int j=0;j<=9;j++){ //枚举低两位
int n = i*1000+i*100+j*10+j; //iijj形式的四位数n
//if(n是完全平方数) cout<<n<<" ";
}
}
return 0;
}
但是会发现要判断“n是完全平方数”不容易实现,可以换一种思路。
思路二:枚举所有四位完全平方数,筛选出其中形如aabb的数:
#include<iostream>
using namespace std;
int main()
{
//条件为空,相当于for(int x=32;true;x++),也就是死循环
for(int x=32; ;x++){
int n = x*x;
if(n>=10000) break; //强制跳出循环
int hi = n/100,lo = n%100; //计算高两位hi,低两位lo
if(hi/10==hi%10 && lo/10==lo%10) cout<<n<<" ";
}
return 0;
}
四、P1980 计数问题
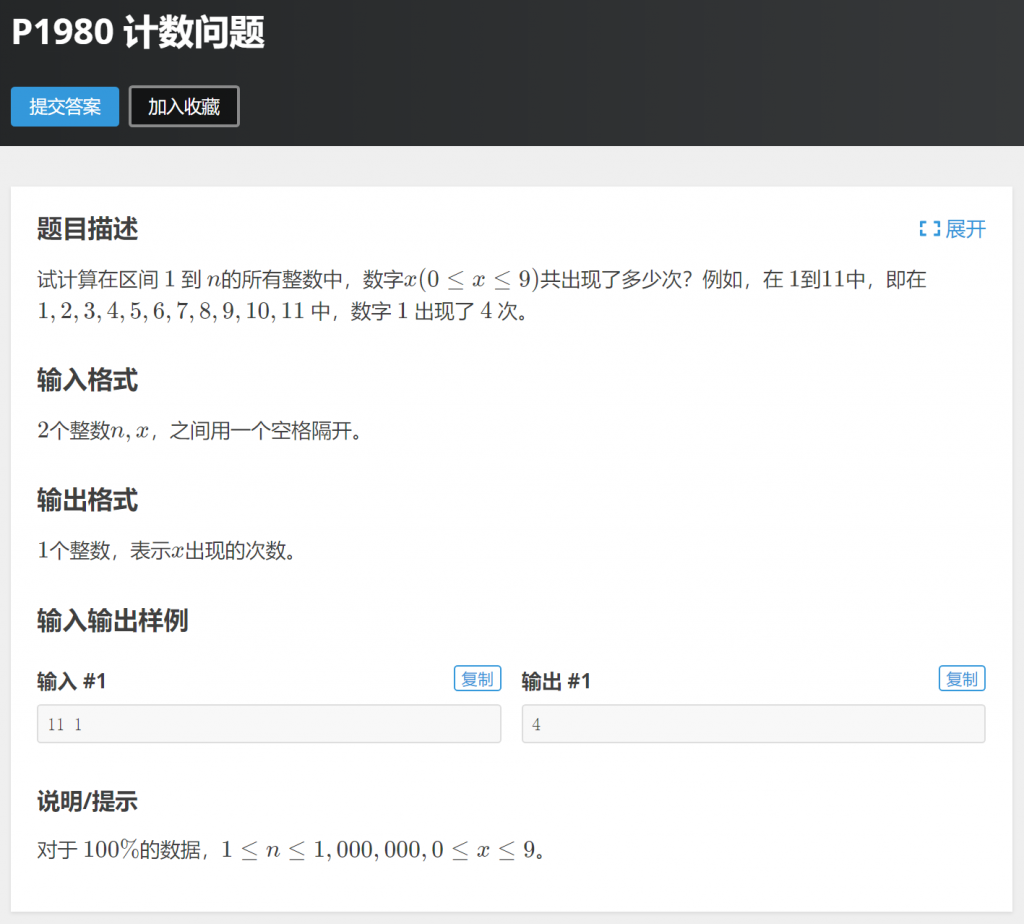
分析:使用循环枚举1~n的每个整数i,对于i,使用while循环拆分出它每位上的数字,如果位上数字等于x则计数:
#include<iostream>
using namespace std;
int main()
{
int n,x,tmp,ans = 0;
cin>>n>>x;
for(int i=1;i<=n;i++){
tmp = i; //tmp赋值成i
//拆分tmp,不会修改i值
while(tmp){
if(tmp%10==x)
ans++;
tmp /= 10;
}
}
cout<<ans;
return 0;
}
下面的程序会出现“死循环”:
#include<iostream>
using namespace std;
int main()
{
int n,x,ans = 0;
cin>>n>>x;
for(int i=1;i<=n;i++){
//拆分i,导致i值被修改
while(i){
if(i%10==x) ans++;
i /= 10;
}
//拆分结束后i值为0
//导致循环出不来
}
cout<<ans;
return 0;
}
五、P5723质数口袋
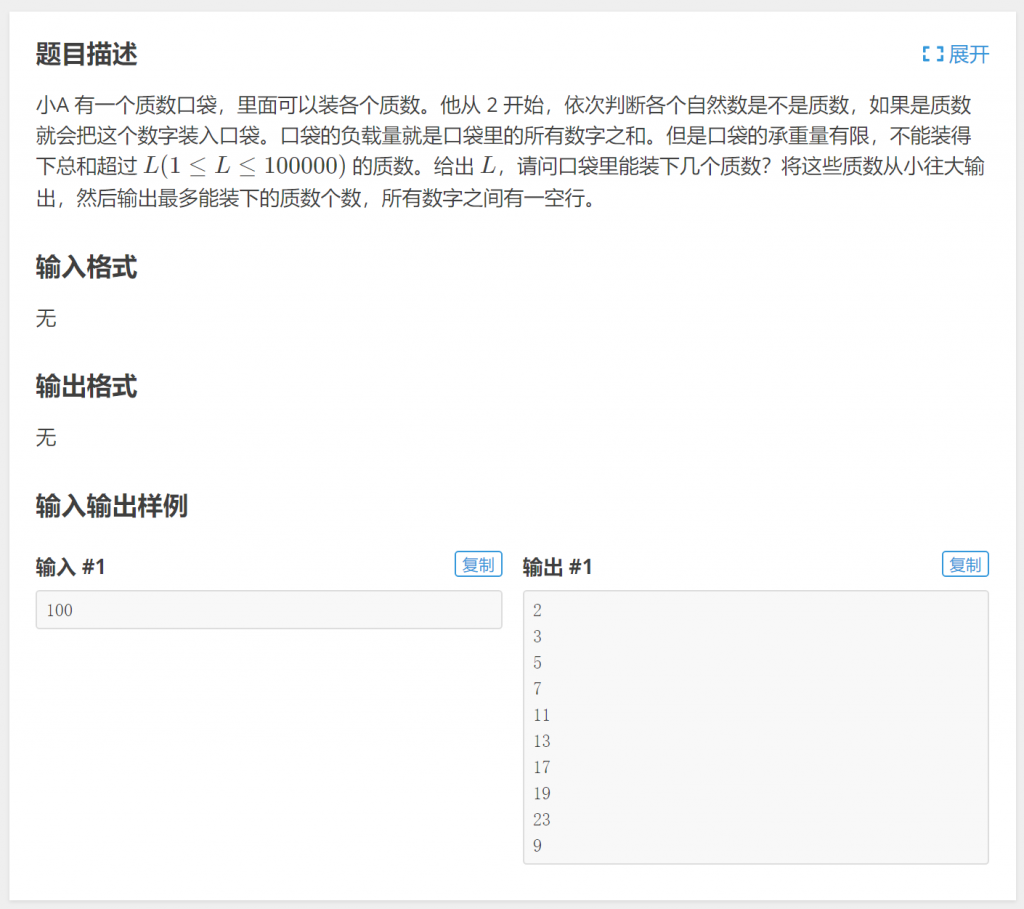
分析:累加器s记录素数和,借助循环处理从2开始的每个整数i,如果i是素数,那么累加到s,累加后如果发现s>L,使用break强制跳出循环。
#include<iostream>
using namespace std;
int main()
{
int L,s = 0,tot = 0;
cin>>L;
for(int i=2;;i++){ //没有写循环条件,则是“死循环”
//判断i是否为素数
int find = 0;
for(int j=2;j*j<=i;j++){
if(i%j==0){
find = 1;
break;
}
}
if(find) continue; //不是素数continue不执行后面的语句直接进入下次循环
s += i;
if(s>L) break; //口袋装不下了,break强制跳出循环
cout<<i<<endl;
tot++;
}
cout<<tot;
return 0;
}
六、P1217 [USACO1.5]回文质数
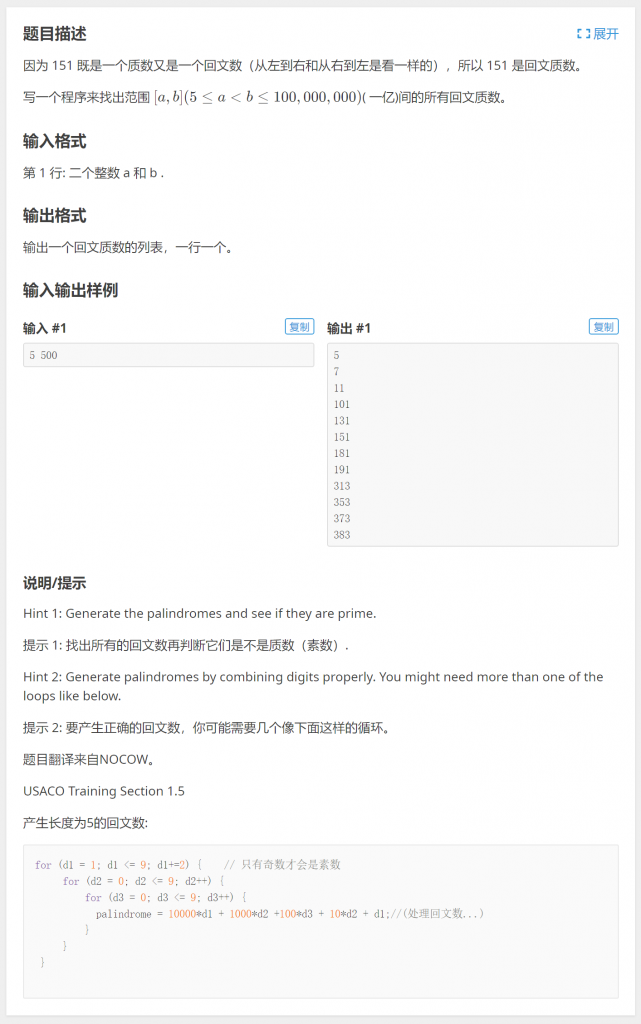
思路一:直接使用循环枚举\([a,b]\)范围内的每个整数\(i\),筛选出既是回文数又是质数的i即可,由此可以得出程序的框架:
for(int i=a;i<=b;i++){
//判断i是回文数
if(i是回文数){
//判断i是质数
if(i是质数){
//输出i
}
}
}
在框架基础上完善各个功能模块,得出程序:
#include<iostream>
using namespace std;
int main()
{
int a,b;
cin>>a>>b;
if(a==1) a++; //避免a==1时后面代码也会输出1
//循环枚举[a,b]范围内每个整数i
for(int i=a;i<=b;i++){
//判断i是否是回文数?
int n = i,m = 0; //n记录i值,后面破坏n的值不破坏i值,这样不会影响外层循环
while(n){ //也就是while(n!=0){
m = m*10+n%10;
n /= 10;
}
if(m==i){ //i是回文数,进一步判断i是否是质数?
int find = 0;
for(int j=2;j*j<=i;j++){
if(i%j==0){
find = 1;
break;
}
}
//i也是质数
if(find==0) cout<<i<<endl;
}
}
return 0;
}
提交代码,会发现最后一个测试点超时:
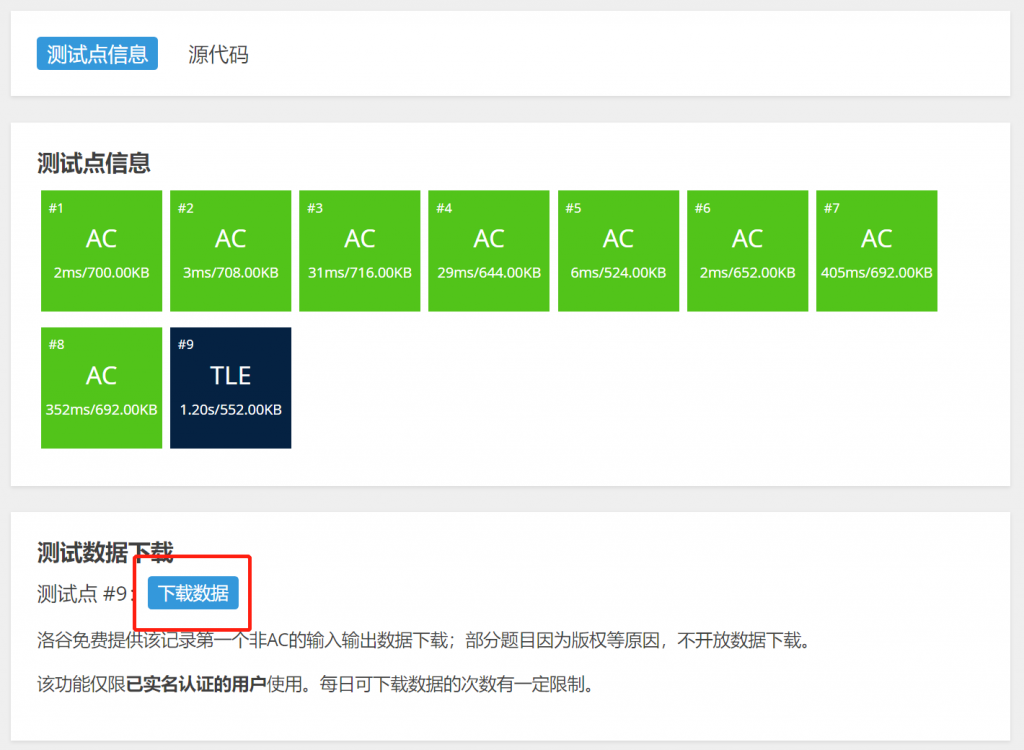
下载该点的测试数据,会发现该点\(a=5,b=100000000\)(其实题目里数据规模也提到了\(b \le 100,000,000\)),外层循环次数接近1亿次,再加上循环体内部的判断回文和判断质数的循环,实际循环重复执行的次数更多!在1s内无法执行完毕导致超时(TLE)。需要优化程序才能通过该测试点。
思路二:优化的策略就是减少循环执行的次数,前面的方法对于\([a,b]\)范围内的每个整数\(i\)都做了测试,其实这里面有大量的非回文数,我们可以通过构造\([a,b]\)范围内回文数的方式来减少循环的执行次数。
例如要构造5位回文数,其实我们只需要使用三重循环枚举个位、十位、百位上的数字即可,因为千位上的数字和十位上数字相同,万位上的数字和个位数的数字相同:
for(int d1=1;d1<=9;d1+=2) //只考虑个位上的数是奇数的情况(个位数是偶数肯定不是质数)
for(int d2=0;d2<=9;d2++)
for(int d3=0;d3<=9;d3++){
int n = d1*10000+d2*1000+d3*100+d2*10+d1;
}
并且这里只需要构造3位、5位、7位回文数并考查是否在\([a,b]\)范围内且是质数,还需要额外考查1位回文质数(5、7)和2位回文质数(11)是否在\([a,b]\)范围内(题目指出\(5 \le a < b \le 100,000,000\),所以不用考虑2)。不需要考虑偶数位的回文数(11除外)是否为质数,因为通过数学知识可知偶数位的回文数都是11的倍数,除11外都不是质数。
#include<iostream>
using namespace std;
int main()
{
int a,b;
cin>>a>>b;
//特殊考虑5、7、11是否在[a,b]范围内
if(a<=5 && b>=5) cout<<5<<endl;
if(a<=7 && b>=7) cout<<7<<endl;
if(a<=11 && b>=11) cout<<11<<endl;
//构造3位回文数
for(int d1=1;d1<=9;d1+=2)//只考虑个位上的数是奇数(个位数是偶数肯定不是质数)
for(int d2=0;d2<=9;d2++){
int n = d1*100+d2*10+d1;
if(n<a) continue; //n<a,不考虑
if(n>b) return 0; //n>b,直接退出程序
int find = 0;
for(int j=2;j*j<=n;j++){
if(n%j==0){
find = 1;
break;
}
}
if(!find) cout<<n<<endl; //if(find==0) cout<<n<<endl;
}
//构造5位回文数
for(int d1=1;d1<=9;d1+=2)
for(int d2=0;d2<=9;d2++)
for(int d3=0;d3<=9;d3++){
int n = d1*10000+d2*1000+d3*100+d2*10+d1;
if(n<a) continue;
if(n>b) return 0;
int find = 0;
for(int j=2;j*j<=n;j++){
if(n%j==0){
find = 1;
break;
}
}
if(!find) cout<<n<<endl;
}
//构造7位回文数
for(int d1=1;d1<=9;d1+=2)
for(int d2=0;d2<=9;d2++)
for(int d3=0;d3<=9;d3++)
for(int d4=0;d4<=9;d4++){
int n = d1*1000000+d2*100000+d3*10000+d4*1000+d3*100+d2*10+d1;
if(n<a) continue;
if(n>b) return 0;
int find = 0;
for(int j=2;j*j<=n;j++){
if(n%j==0){
find = 1;
break;
}
}
if(!find) cout<<n<<endl;
}
return 0;
}
思路三:筛选法求质数。在后面章节数组的内容中会详细介绍。
 NOIP学习小站
NOIP学习小站