前面介绍的都是一维数组,一维数组就像“一排容器”,能够存储若干相同数据类型的数据。对应的还有二维数组、三维数组……多维数组相当于一片容器的矩阵。
一、二维数组
前面介绍了一维数组就像“一排容器”,可以描述为一种“线性”的结构,那么二维数组就像一个有行有列的阵列(矩阵)。
1.二维数组的定义
定义二维数组的方法很简单:数组类型 数组变量名[第一维长度][第二维长度];,例如:
int a[3][5]; long long b[4][100],c[10000][100000]; double d[1001]; char strs[1001][101];
以int a[3][5];为例,二维数组中的元素往往描述成有行有列的矩阵(虽然在内存中仍然是线性存储的),每个元素按照矩阵方式排列如下:
| 第0列 | 第1列 | 第2列 | 第3列 | 第4列 | |
| 第0行 | a[0][0] | a[0][1] | a[0][2] | a[0][3] | a[0][4] |
| 第1行 | a[1][0] | a[1][1] | a[1][2] | a[1][3] | a[1][4] |
| 第2行 | a[2][0] | a[2][1] | a[2][2] | a[2][3] | a[2][4] |
由此可知,定义二维数组时数组类型 数组变量名[第一维长度][第二维长度];,第一维长度对于矩阵的行,第二维长度对应矩阵的列。二维数组元素的使用仍然是使用下标,不过有两个[],两个[]中内容依次是第一维下标和第二维下标。
2.二维数组元素的使用
二维数组中的元素和一维数组的元素一样,可以理解成二维数组中的特殊变量,除了书写时比较特殊外,使用方法和普通变量一致:
int a[10][5];
a[0][0] = 100;
cin>>a[0][1];
a[0][2] = a[0][0]*a[0][1];
cout<<a[0][1]<<endl;
cout<<a[0][1]+a[0][2]<<endl;
//使用双重循环输入数据到数组中
for(int i=0;i<10;i++){
for(int j=0;j<5;j++){
cin>>a[i][j];
}
}
//使用双重循环按照行列形式输出数组中的每个元素
for(int i=0;i<10;i++){
for(int j=0;j<5;j++){
cout<<a[i][j]<<" ";
}
cout<<endl;
}
二、二维数组例题
1. 鞍点的数量

分析:用二维数组来存储矩阵,使用双重循环遍历二维数组的每个元素,判断元素是否是鞍点(是所在行的最大值,也是所在列的最大值)并计数。
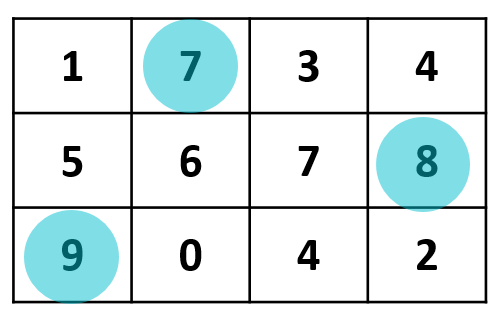
那么对于第\(i\)行\(j\)列的元素,如何判断是否是鞍点呢?可以扫描第\(i\)行的所有元素,看看能否找到比它大的元素,如果没有,那这个元素就是所在行的最大值。同理扫描第\(j\)列的所有元素,看看能否找到比它大的元素,如果没有,那这个元素就是所在列的最大值。
#include<iostream>
using namespace std;
int a[1010][1010];
int main()
{
int N,M;
cin>>N>>M;
for(int i=1;i<=N;i++){
for(int j=1;j<=M;j++){
cin>>a[i][j];
}
}
int ans = 0;
//使用双重循环遍历二维数组,依次判断每个元素是否是鞍点
for(int i=1;i<=N;i++){
for(int j=1;j<=M;j++){
//判断a[i][j]是第i行最大值
bool f1 = true;
for(int k=1;k<=M;k++){
if(a[i][j]<a[i][k]){
f1 = false;
break;
}
}
//判断a[i][j]是第j列最大值
bool f2 = true;
for(int k=1;k<=N;k++){
if(a[i][j]<a[k][j]){
f2 = false;
break;
}
}
//a[i][j]是鞍点
if(f1==true && f2==true){
ans++;
}
}
}
cout<<ans<<endl;
return 0;
}
分析上面程序,可知算法时间复杂度是\(O(N*M*(N+M))\)。还有更高效的做法。可以计算出每行、每列的最大值存放到一维数组中,那么对于第\(i\)行\(j\)列的元素,如果值与第\(i\)行最大值相等并且值与第\(j\)列最大值相等,那么它就是一个鞍点。这样可以将算法时间复杂度优化到\(O(N*M)\)。
#include<iostream>
using namespace std;
int a[1010][1010];
//rowm记录每行最大值,colm记录每列最大值
int rowm[1010],colm[1010];
int main()
{
int N,M;
cin>>N>>M;
for(int i=1;i<=N;i++){
for(int j=1;j<=M;j++){
cin>>a[i][j];
}
}
//计算每行最大值(行优先遍历)
for(int i=1;i<=N;i++){
rowm[i] = a[i][1];
for(int j=2;j<=M;j++){
if(a[i][j]>rowm[i]) rowm[i] = a[i][j];
}
}
//计算每列最大值(列优先遍历)
for(int j=1;j<=M;j++){
colm[j] = a[1][j];
for(int i=2;i<=N;i++){
if(a[i][j]>colm[j]) colm[j] = a[i][j];
}
}
//使用双重循环遍历二维数组,依次判断每个元素是否是鞍点
int ans = 0;
for(int i=1;i<=N;i++){
for(int j=1;j<=M;j++){
if(a[i][j]==rowm[i] && a[i][j]==colm[j]){
ans++;
}
}
}
cout<<ans<<endl;
return 0;
}
2.买钢笔

分析:要买尽量多的铅笔,那么应该优先考虑多买 4 元钱的钢笔,剩余的钱数可能是0,1,2,3,可以使用多分支语句或者switch...case语句来进行分类讨论:
#include<iostream>
using namespace std;
int main()
{
int x,a,b,c;
cin>>x;
c = x/4;
a = b = 0;
int mod = x%4;
if(mod == 1){
b++;c--;
}else if(mod == 2){
a++,c--;
}else if(mod == 3){
a++,b++,c-=2;
}
cout<<a<<" "<<b<<" "<<c<<endl;
return 0;
}
#include<iostream>
using namespace std;
int main()
{
int x,a,b,c;
cin>>x;
c = x/4;
a = b = 0;
switch(x%4){
case 1:b++;c--;break;
case 2:a++,c--;break;
case 3:a++;b++;c-=2;break;
}
cout<<a<<" "<<b<<" "<<c<<endl;
return 0;
}
这里也可以使用数组来解决问题,此时甚至可以不使用分支结构(大家自行分析下面的程序):
#include<iostream>
using namespace std;
int main()
{
int x;
cin>>x;
int ans[3] = {0,0,x/4};
int change[4][3] = {
{0,0,0},
{0,1,-1},
{1,0,-1},
{1,1,-2},
};
int mod = x%4;
for(int i=0;i<3;i++)
cout<<ans[i]+change[mod][i]<<" ";
cout<<endl;
return 0;
}
3.阵列方格
来看一个例题:给定正整数\(n,m,i,j\)(\(1 \le n,m \le 1000\),\(1 \le i \le n\),\(1 \le j \le m\)),在\(n\)行\(m\)列的方格阵列中,找出与第\(i\)行第\(j\)列方格(记为\((i,j)\),行列序号均从1开始计数)同行、同列、同对角线的所有方格(不包括\((i,j)\)自身),这样的方格很多,要求按照行列的顺序输出。
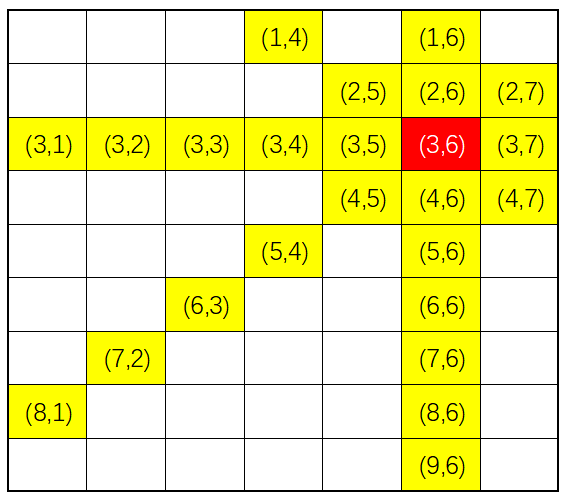
如左侧图解,\(n=9,m=7\),图中标识出了与\((3,6)\)这个方格同行、同列、同对角线的所有方格,那么输出的内容应该是:\((1,4)\)、\((1,6)\)、\((2,5)\)、\((2,6)\)、…、\((8,1)\)、\((8,6)\)、\((9,6)\)。
如果问题要求是先输出所用同行、然后输出同列,然后输出同对角线的方格,其实是可以使用先后的四个循环依次输出这些方格。但是题目要求的是按照行列的顺序输出,也就是四类方格是混在一起的,直接使用循环暂时没有思路,可以试试使用二维数组来处理。
我们可以使用二维数组int a[1001][1001];中的元素a[x][y]来标记方格阵列中第\(x\)行第\(y\)列方格\((x,y)\)是否满足条件。开数组的时候直接使用了最大数据规模,并且考虑了要使用的下标与自然序列一致(第一维长度、第二维长度都比数据规模多开1)。
最开始的时候将数组a每个元素都赋值为0,表示每个方格都不符合条件,然后将与方格\((i,j)\)同行、同列、同对角线的方格对应的数组元素都标记成1。最后使用双重循环按照行列的顺序依次筛选输出值为1的数组元素对应的方格坐标即可。
同行同列的方格容易找出来,对角线上的方格如何找出来呢?
思路一:分别查找标记方格\((i,j)\)左侧对角线和右侧对角线上的方格:
#include<iostream>
using namespace std;
int a[1001][1001]; //全局int类型数组,默认每个元素值都是0,正好表示筛选前都不符合条件
int main()
{
int n,m,i,j;
cin>>n>>m>>i>>j;
//标记同行方格满足条件
for(int y=1;y<=m;y++) a[i][y] = 1;
//标记同列方格满足条件
for(int x=1;x<=n;x++) a[x][j] = 1;
//左侧对角线上的方格(从第j-1列依次到第1列)
for(int y=j-1;y>=1;y--){
int d = j-y;
int x = i+d; //第【y】列对角线【左下方位】的方格x坐标
if(x>=1 && x<=n) a[x][y] = 1;
x = i-d; //第【y】列对角线【左上方位】的方格x坐标
if(x>=1 && x<=n) a[x][y] = 1;
}
//右侧对角线上的方格(从第j+1列依次到第m列)
for(int y=j+1;y<=m;y++){
int d = y-j;
int x = i+d; //第【y】列对角线【右下方位】的方格x坐标
if(x>=1 && x<=n) a[x][y] = 1;
x = i-d; //第【y】列对角线【右上方位】的方格x坐标
if(x>=1 && x<=n) a[x][y] = 1;
}
a[i][j] = 0; //本身不输出,排除掉(前面被标记过)
//查找数组值为1的元素,输出对应方格坐标
for(int x=1;x<=n;x++){
for(int y=1;y<=m;y++){
if(a[x][y]==1) cout<<"("<<x<<","<<y<<")"<<" ";
}
cout<<endl;
}
return 0;
}
思路二:从第一列开始依次查找标记每列上对角线上的方格:
#include<iostream>
using namespace std;
int a[1001][1001]; //全局int类型数组,默认每个元素值都是0,正好表示筛选前都不符合条件
int main()
{
int n,m,i,j;
cin>>n>>m>>i>>j;
//标记同行方格满足条件
for(int y=1;y<=m;y++) a[i][y] = 1;
//标记同列方格满足条件
for(int x=1;x<=n;x++) a[x][j] = 1;
//从第1列开始查找每一列上满足条件的方格(在对角线上)
for(int y=1;y<=m;y++){
int d = y-j;
int x = i+d;
if(x>=1 && x<=n) a[x][y] = 1;
x = i-d;
if(x>=1 && x<=n) a[x][y] = 1;
}
a[i][j] = 0; //本身不输出,排除掉(前面被标记过)
//查找数组值为1的元素,输出对应方格坐标
for(int x=1;x<=n;x++){
for(int y=1;y<=m;y++){
if(a[x][y]==1) cout<<"("<<x<<","<<y<<")"<<" ";
}
cout<<endl;
}
return 0;
}
其实思路一仍然是依次查找了每列对角线上的方格,只不过分成了左侧和右侧两部分来分别查找。思路二则将两部分整合,直接从第一列依次查找每列对角线上的方格。可以先看右侧对角线第\(y\)列的两个坐标点:
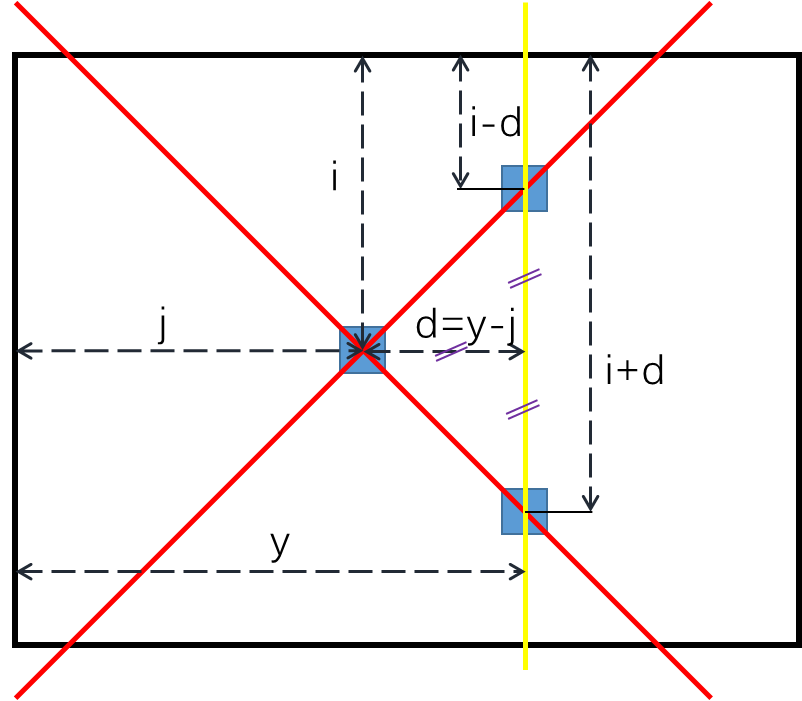
上面的计算方法其实对于左边对角线上的点同样适用。
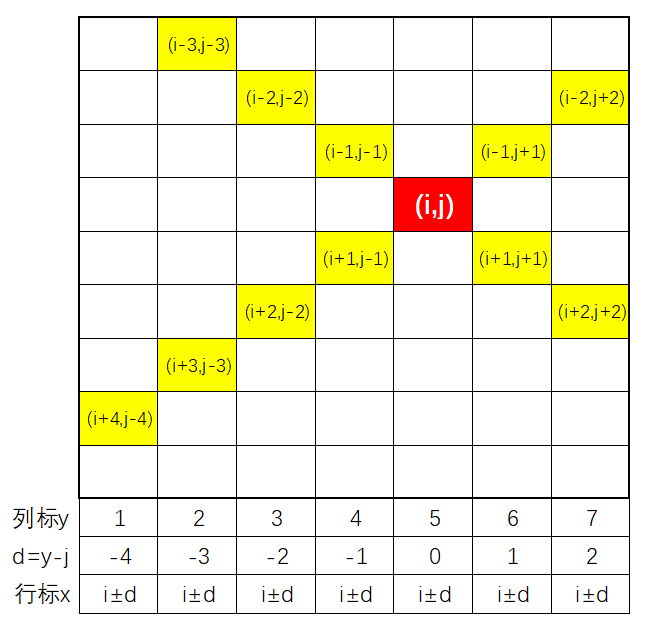
可以通过右侧的图解分析可知:
设列标为\(y\),记\(d = y-j\),那么可知第\(y\)列\((i,j)\)对角线上的两个方格的行坐标应该是\(i+d\)和\(i-d\),还需要考虑行坐标是否在\([1,n]\)范围内。
这个时候我们猛然发现,每一列上满足条件的方格其实是可以计算出来的!同样地,每一行上满足条件的方格也能计算出来。
通过上面的分析可知这个问题不用数组也能解决,通过查找规律可以借助循环一行一行地找出每行符合条件的方格:
#include<iostream>
using namespace std;
int main()
{
int n,m,i,j;
cin>>n>>m>>i>>j;
//依次查找每一行符合条件的方格
for(int x=1;x<=n;x++){ //x是行标
if(x!=i){ //不是第i行
int d = i-x;
if(d<0) d = -d; //d是第i行与第x行的距离
//通过分析查找规律可知第x行在(x,j)左侧且在(i,j)对角线上的方格是(x,j-d)
//第x行在(x,j)右侧且在(i,j)对角线上的方格是(x,j+d)
//考查对角线上的方格(x,j-d)是否在阵列范围内(没有越界)
if(j-d>=1) cout<<"("<<x<<","<<j-d<<") ";
cout<<"("<<x<<","<<j<<") "; //(x,j)与(i,j)同列
//考查对角线上的方格(x,j+d)是否在阵列范围内(没有越界)
if(j+d<=m) cout<<"("<<x<<","<<j+d<<") ";
}else{ //第i行
//除了(x,j)都输出:因为x==i,(x,j)就是(i,j)
for(int y=1;y<=m;y++){
if(y!=j) cout<<"("<<x<<","<<y<<") ";
}
}
cout<<endl;
}
return 0;
}
4.洛谷P5728 旗鼓相当的对手
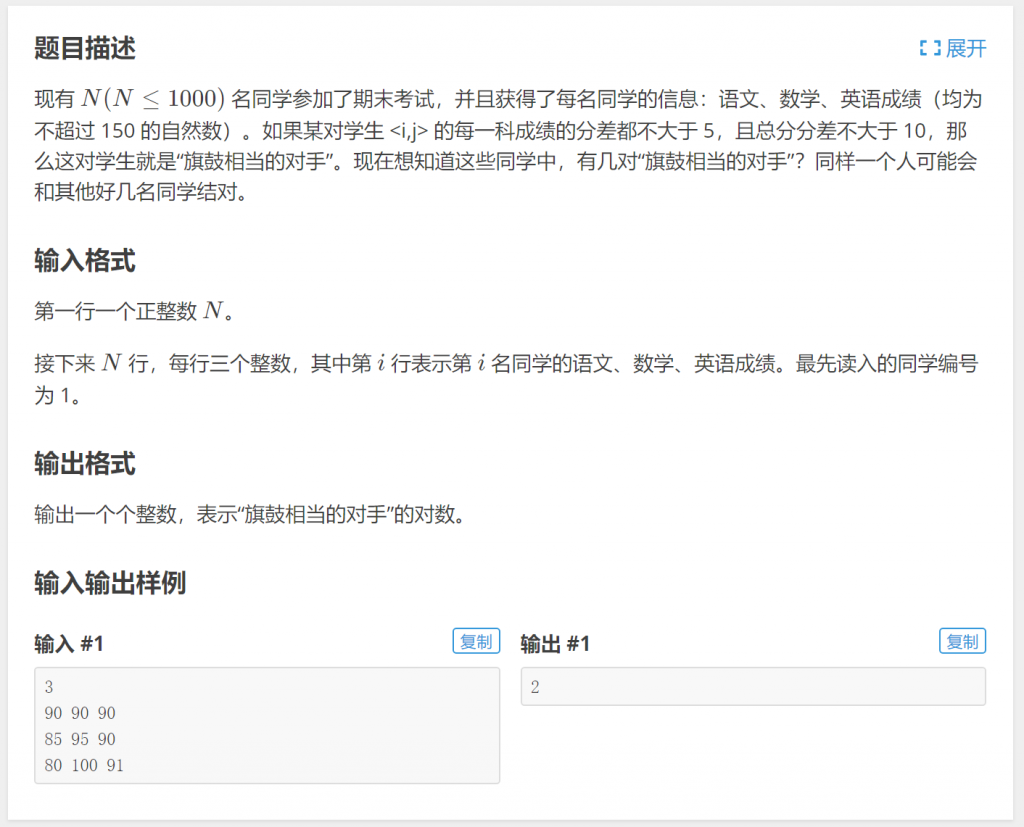
分析:使用二维数组int a[1000][4];保存每位同学三门科目的考试成绩和总成绩,每位同学的成绩占二维数组一行。同学两两组合考虑是否是旗鼓相当的对手,为了避免重复考虑,对于第0~\(N-2\)的第\(i\)位同学,考虑并统计他与第\(i+1\)~\(N-1\)的每位同学是否是旗鼓相当的对手即可。
#include<iostream>
#include<cmath>
using namespace std;
int a[1000][4];
int main()
{
int N,s1,s2,ans = 0;
cin>>N;
for(int i=0;i<N;i++){
cin>>a[i][0]>>a[i][1]>>a[i][2];
a[i][3] = a[i][0]+a[i][1]+a[i][2]; //计算总分
}
for(int i=0;i<N-1;i++){
for(int j=i+1;j<N;j++){
bool f = abs(a[i][3]-a[j][3])<=10; //总分之差不大于10
for(int k=0;f && k<3;k++){ //借助循环判断3门学科
f = f && (abs(a[i][k]-a[j][k])<=5); //每门学科成绩之差不大于5
}
if(f) ans++;
}
}
cout<<ans;
return 0;
}
代码中判断“旗鼓相当”的语句大家可以仔细琢磨:
bool f = abs(a[i][3]-a[j][3])<=10; //总分之差不大于10
for(int k=0;f && k<3;k++){ //借助循环判断3门学科
f = f && abs(a[i][k]-a[j][k])<=5; //每门学科成绩之差不大于5
}
if(f) ans++;
甚至还可以进一步让该“旗鼓相当”的判断更加工整:
#include<iostream>
#include<cmath>
using namespace std;
int a[1000][4];
int b[4] = {5,5,5,10}; //记录每门学科最大差值和总分最大差值
int main()
{
int N,s1,s2,ans = 0;
cin>>N;
for(int i=0;i<N;i++){
cin>>a[i][0]>>a[i][1]>>a[i][2];
a[i][3] = a[i][0]+a[i][1]+a[i][2]; //计算总分
}
for(int i=0;i<N-1;i++){
for(int j=i+1;j<N;j++){
bool f = true;
for(int k=0;f && k<4;k++){
f = f && (abs(a[i][k]-a[j][k])<=b[k]);
}
if(f) ans++;
}
}
cout<<ans;
return 0;
}
如果不易理解,其实上面判断“旗鼓相当”的代码也可以写成下面虽然繁琐但简单的代码:
if(abs(a[i][0]-a[j][0])<=5 && abs(a[i][1]-a[j][1])<=5 && abs(a[i][2]-a[j][2])<=5 && abs(a[i][3]-a[j][3])<=10) ans++;
三、多维数组
回顾一维数组、二维数组的定义和元素的使用方法,不难得出更高维数组的定义和元素的使用方法。
一维数组的使用举例
int a[11];
a[1] = 123;
cin>>a[2];
a[3] = a[1]*a[2];
cout<<a[3];
cout<<a[3]*a[1];
//使用循环输入数据到数组中
for(int i=1;i<=10;i++){
cin>>a[i];
}
//使用循环输出数组中的每个元素
for(int i=1;i<=10;i++){
cout<<a[i]<<" ";
}
二维数组的使用举例
int a[10][5];
a[0][0] = 100;
cin>>a[0][1];
a[0][2] = a[0][0]*a[0][1];
cout<<a[0][1]<<endl;
cout<<a[0][1]+a[0][2]<<endl;
//使用双重循环输入数据到数组中
for(int i=0;i<10;i++){
for(int j=0;j<5;j++){
cin>>a[i][j];
}
}
//使用双重循环按照行列形式输出数组中的每个元素
for(int i=0;i<10;i++){
for(int j=0;j<5;j++){
cout<<a[i][j]<<" ";
}
cout<<endl;
}
通过一个例子来看三维数组的使用:洛谷P5729 工艺品制作
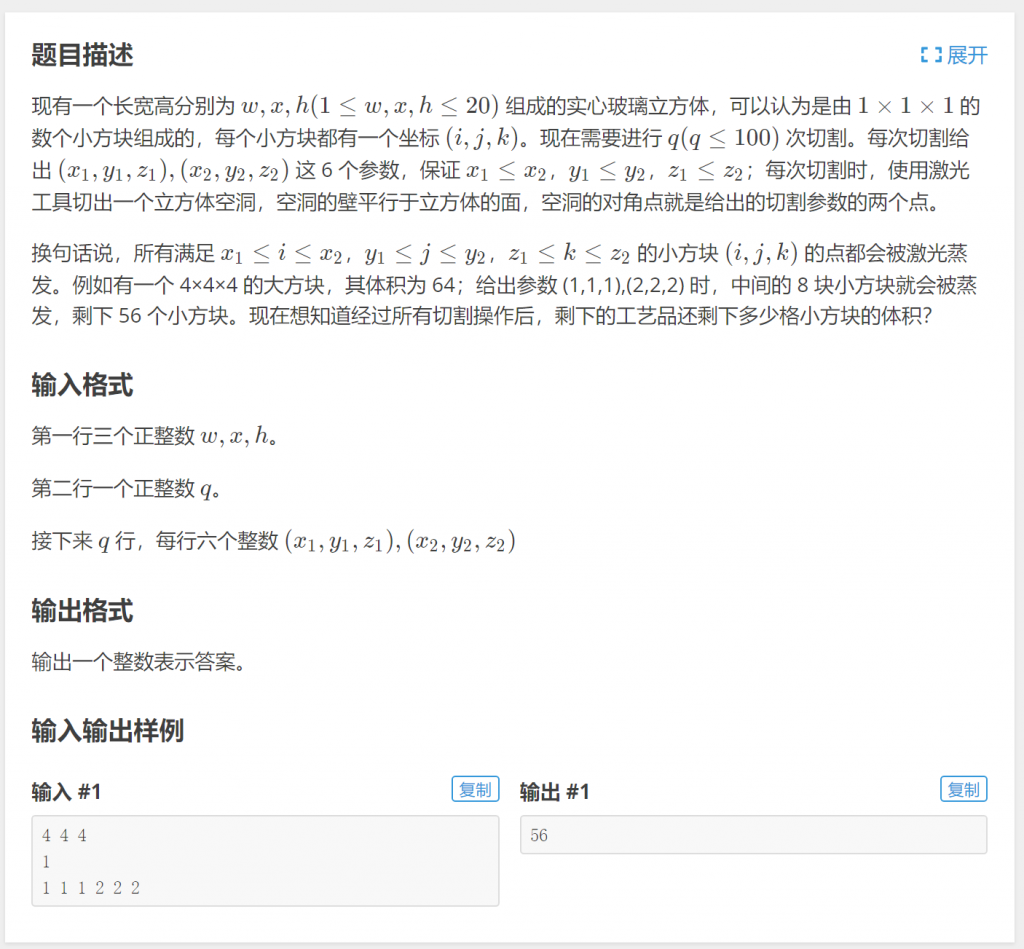
分析:使用三维数组记录每个小方块是否被蒸发(最开始都没有被蒸发,元素都标记为0),对于每一次操作,相当于把一个小的立方体中的每个小方块蒸发掉(标记为1)。所有操作完成后,统计三维数组中值为0的元素的个数即可。
#include<iostream>
#include<cmath>
using namespace std;
//三维全局数组v,元素v[i][j][k]记录坐标点(i,j,k)小方块是否被蒸发掉
//全局数组所有元素默认值为0,正好表示开始时都没有被蒸发
int v[21][21][21];
int main()
{
int w,x,h,q,ans = 0;
int x1,y1,z1,x2,y2,z2;
cin>>w>>x>>h;
cin>>q;
while(q--){ //q次重复操作
cin>>x1>>y1>>z1>>x2>>y2>>z2;
//坐标范围描述的小立方体中的每个小方块都被蒸发掉,使用三重循环处理
for(int i=x1;i<=x2;i++){
for(int j=y1;j<=y2;j++){
for(int k=z1;k<=z2;k++){
v[i][j][k] = 1; //标记(i,j,k)小方块被蒸发掉
}
}
}
}
for(int i=1;i<=w;i++){
for(int j=1;j<=x;j++){
for(int k=1;k<=h;k++){
ans += 1-v[i][j][k]; //统计未蒸发小方块数量
}
}
}
cout<<ans;
return 0;
}
 NOIP学习小站
NOIP学习小站