数组例题——筛选法求素数

前面介绍过如何判断一个正整数是否是素数，如果我们要筛选出\([1,n]\)范围内的所有素数，前面介绍的方法是使用循环枚举每一个整数\(i\)并在循环体中使用循环来判断\(i\)是否为素数：

#include<iostream>
using namespace std; 
int main()
{
	int n;
	cin>>n;
	for(int i=2;i<=n;i++){
		int find = 0;
		for(int j=2;j*j<=i;j++){
			if(i%j==0){
				find = 1;
				break;
			}
		}
		if(find==0) cout<<i<<" ";
	} 
    return 0;
}

其实还有一种效率更高的方法——筛选法。具体步骤如下：

首先将\([1,n]\)（这里以\([1,100]\)为例）的所有整数书写出来：

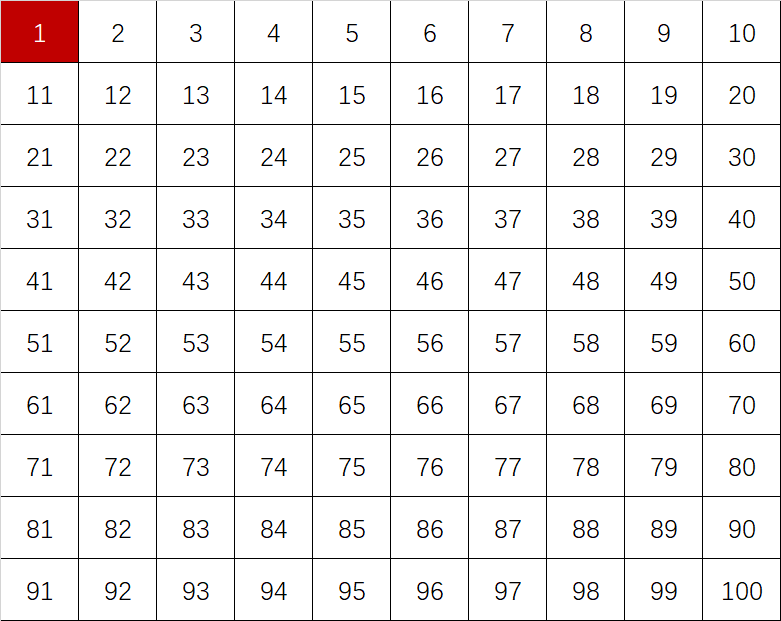
首先划去2的倍数（不包括2）：

然后划去3的倍数（同样不包括3）：

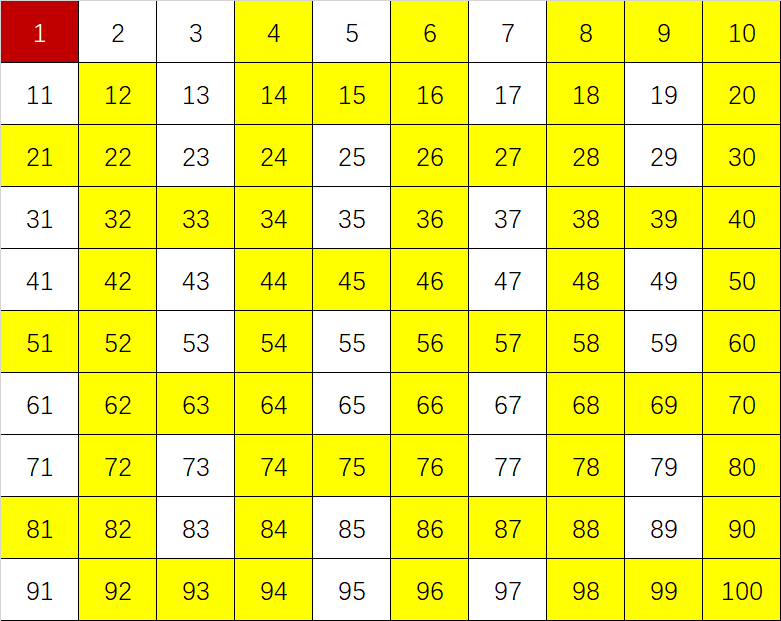
接下来，因为4已经被划去了，不用考虑，然后划去5的倍数（不包括5）：

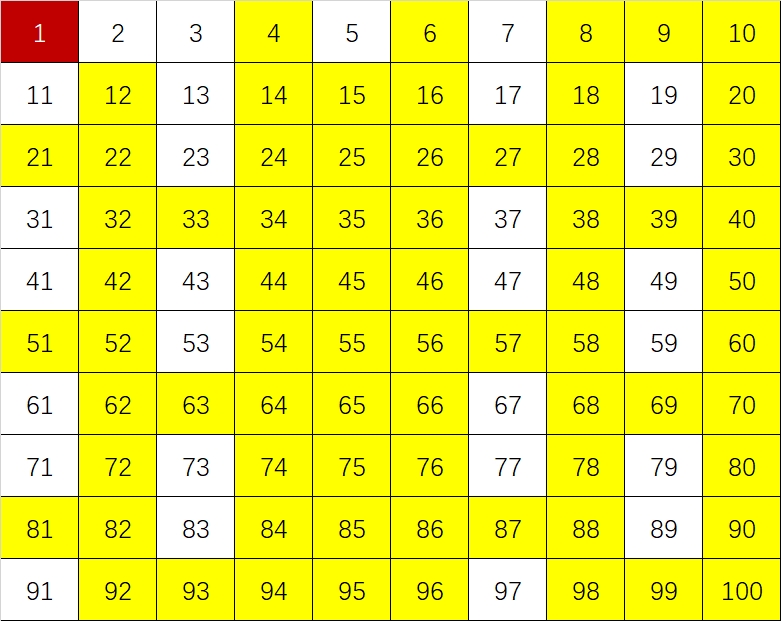
接一下依次考虑后面的数，只要没被划掉，那就把这个数的倍数划去（不包括自身）。最后一个考虑的数是\(\sqrt{100}\)，也就是10（不用考察到最后一个数100）。全部处理后结果如下：

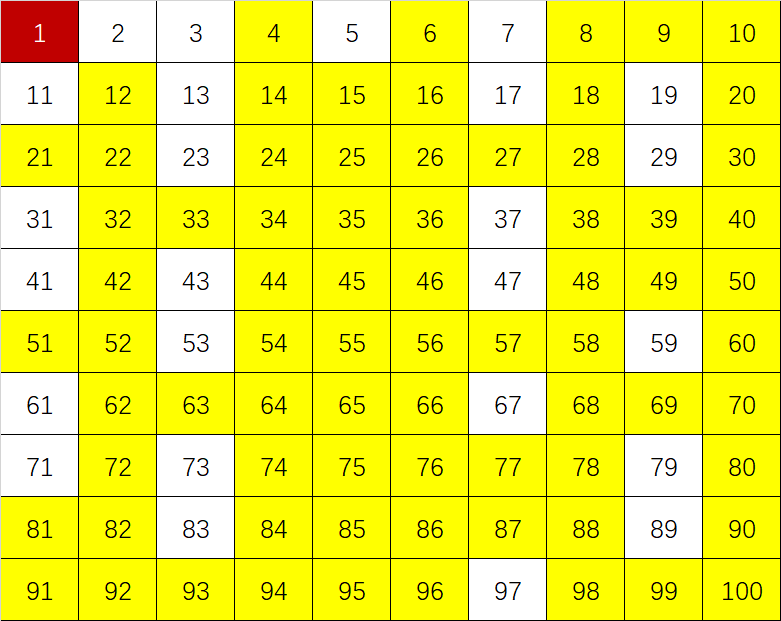
可以使用数组来记录整数是否被划掉，根据上述步骤可以得出参考程序：

#include<iostream>
using namespace std;
const int N = 10000; 
int a[N+1];   //全局数组元素a[i]记录整数i是否被划掉，默认值为0，正好表示没有被划掉 
int main()
{
	int n;
	cin>>n;
	a[1] = 1;    //1不是素数，划掉
	for(int i=2;i*i<=n;i++){   //从2开始考察，一直到sqrt(n)
		//考察整数i
		if(a[i]==0){	//数字i没有被划掉 
			//把i的2倍,3倍,4倍,…,的数都划掉 
			for(int j=i+i;j<=N;j+=i){
				a[j]=1;
			}
		}
	}
	for(int i=1;i<=n;i++){
		if(a[i]==0) cout<<i<<" ";    //如果i没有被划掉，输出i
	}
    return 0;
}

其实还可以通过线性筛（欧拉筛）算法来提高程序执行效率，线性筛算法的思路是：从2到\(n\)的每一个整数（无论质数合数）\(i\)，筛掉　小于\(i\)的最小质因子的所有质数　的\(i\)倍的数（由此可见数学理论对算法设计的重要性）。

例如筛选过程中考察到整数77，77分解质因数是\(7 \times 11\)，最小质因子是7，那么需要筛掉所有小于7的质数（2、3、5）的77倍的那些整数，也就是筛掉\(2 \times 77\)、\(3 \times 77\)、\(5 \times 77\)。

#include<iostream>
using namespace std;
const int N = 10000; 
int a[N+1];   //全局数组元素a[i]记录整数i是否被筛去
int b[N+1];   //全局数组b记录所有素数 
int main()
{
	//cnt计数器，记录找到素数的个数
	int n,cnt = 0;
	cin>>n;
	for(int i=2;i<=n;i++){
		if(a[i]==0) b[cnt++] = i;  //i没有被筛掉，是素数，记录到数组b中
		
		//将记录素数的数组b每个元素的i倍筛掉 
		for(int j=0;j<cnt && i*b[j]<=n;j++){
			a[b[j]*i] = 1;        //筛掉b[j]的i倍
			if(i%b[j]==0) break;  //只考虑数组b中小于i的最小质因子的那些素数 
		}
	}
	for(int i=0;i<cnt;i++){
		cout<<b[i]<<" ";
	}
    return 0;
}