数组例题——斐波那契数列-NOIP学习小站

在700多年前，意大利有一位著名数学家斐波那契在他的《算盘全集》一书中提出了这样一道有趣的兔子繁殖问题：兔子在出生两个月以后，就具有生殖后代的能力。假设一对兔子，每月都能生一对兔子，生出来的每一对小兔子，在出生两个月后，也每月生一对兔子。那么，由一对刚出生的小兔子开始，连续不断地繁殖下去，在某个指定的月份有多少对兔子？

通过表格来分析：

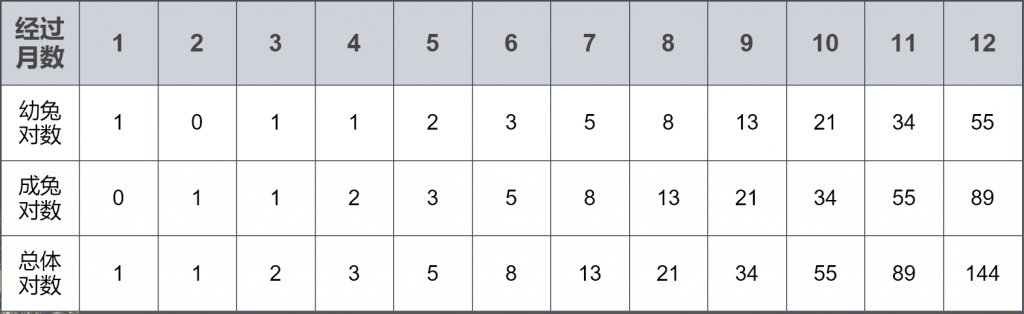
通过最后一行的分析，可知，第1、2个月后，兔子的对数都是1，从第3个月开始，兔子的对数是前面两个月的和。如果第\(n\)个月后兔子的对数用\(a_n\)来表示，用高中数列的知识来描述，有：

\( a_n=\left\{ \begin{aligned} 1(n=1,2) \\ a_{n-1}+a_{n-2}(n>=3) \end{aligned} \right. \)

我们可以借助三个变量来依次推导计算：

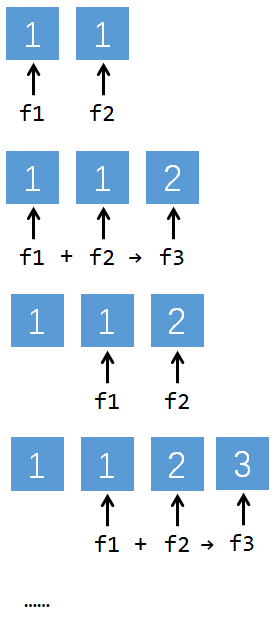
开始时：\(f1=1,f2=1\)

在计算过程中重复执行以下步骤：

\(f3=f2+f1\)
\(f1=f2\)
\(f2=f3\)

注意第2步和第3步顺序不能交换！

这样依次推导的算法，称为递推算法。

#include<iostream>

using namespace std;

int main()

{

int n;

long long f1,f2,f3; //值增加较快，使用long long

cin>>n;

f1 = f2 = 1;

if(n>=1) cout<<1<<":"<<f1<<endl;

if(n>=2) cout<<2<<":"<<f2<<endl;

f3 = f2+f1;

cout<<i<<":"<<f3<<endl;

f1 = f2;

f2 = f3;

}

return 0;

}

#include<iostream> using namespace std; int main() { int n; long long f1,f2,f3; //值增加较快，使用long long cin>>n; f1 = f2 = 1; if(n>=1) cout<<1<<":"<<f1<<endl; if(n>=2) cout<<2<<":"<<f2<<endl; for(int i=3;i<=n;i++){ f3 = f2+f1; cout<<i<<":"<<f3<<endl; f1 = f2; f2 = f3; } return 0; }

#include<iostream>
using namespace std;
int main()
{
	int n;
	long long f1,f2,f3;     //值增加较快，使用long long
	cin>>n;
	f1 = f2 = 1;
	
	if(n>=1) cout<<1<<":"<<f1<<endl;
	if(n>=2) cout<<2<<":"<<f2<<endl;
	
	for(int i=3;i<=n;i++){
		f3 = f2+f1;
		cout<<i<<":"<<f3<<endl;
		f1 = f2;
		f2 = f3;
	}
    return 0;
}

当然可以使用数组来解决问题：

#include<iostream>

using namespace std;

long long a[93] = {0,1,1}; //数组元素部分赋值

int main()

{

int n;

cin>>n;

for(int i=3;i<=n;i++) a[i] = a[i-1]+a[i-2];

for(int i=1;i<=n;i++) cout<<i<<":"<<a[i]<<endl;

return 0;

}

#include<iostream> using namespace std; long long a[93] = {0,1,1}; //数组元素部分赋值 int main() { int n; cin>>n; for(int i=3;i<=n;i++) a[i] = a[i-1]+a[i-2]; for(int i=1;i<=n;i++) cout<<i<<":"<<a[i]<<endl; return 0; }

#include<iostream>
using namespace std;
long long a[93] = {0,1,1};  //数组元素部分赋值 
int main()
{
	int n;
	cin>>n;
	for(int i=3;i<=n;i++) a[i] = a[i-1]+a[i-2];
	for(int i=1;i<=n;i++) cout<<i<<":"<<a[i]<<endl;
    return 0;
}

其实斐波那契数列有通项公式：

\(a_n = \dfrac{1}{\sqrt{5}}\left[\left({\dfrac{1+\sqrt{5}}{2}}\right)^n-\left({\dfrac{1-\sqrt{5}}{2}}\right)^n\ \right]\)

又称为“比内公式”，是用无理数表示有理数的一个范例。

一	二	三	四	五	六	日
	1	2	3	4	5	6
7	8	9	10	11	12	13
14	15	16	17	18	19	20
21	22	23	24	25	26	27
28	29	30	31

其他操作

切换注册登录

用户名或邮箱

密码

切换登录注册

昵称

邮箱