数组例题——杨辉三角

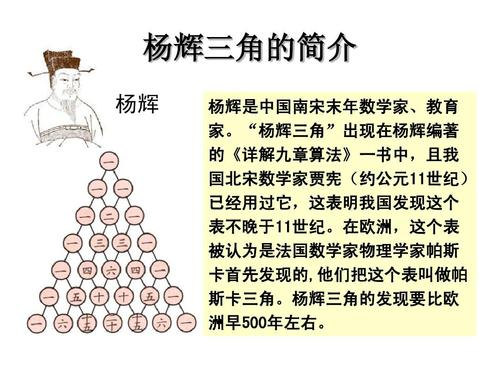
杨辉三角，是二项式系数在三角形中的一种几何排列。在欧洲，这个表叫做帕斯卡三角形。帕斯卡（1623——1662）是在1654年发现这一规律的，比杨辉要迟393年，比贾宪迟600年。杨辉三角是中国古代数学的杰出研究成果之一，它把二项式系数图形化，把组合数内在的一些代数性质直观地从图形中体现出来，是一种离散型的数与形的优美结合。

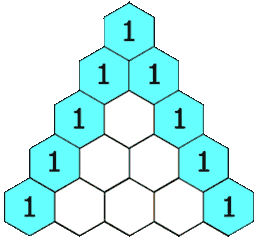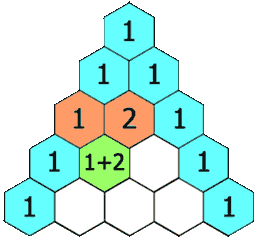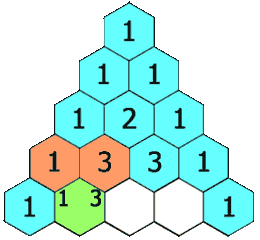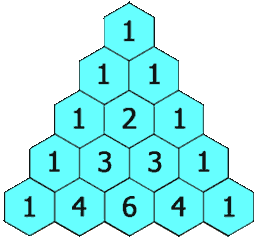
现在要输出杨辉三角形前\(n\)行（\(1 \le n \le 20\)）。

分析：杨辉三角形每一行第1个和最后一个数都是1，中间的数是上一行“肩上”两数的和。可以使用二维数组a存储杨辉三角形，第\(i\)行第\(j\)个数字存储在数组元素a[i][j]中，可知当j==1 或者 j==i时a[i][j]=1；否则a[i][j] = a[i-1][j-1]+a[i-1][j];

#include<iostream>
using namespace std;
int a[21][21];
int main()
{
	int n;
	cin>>n;
	 
    a[1][1] = 1;	//第1行
	//使用循环计算第2～n行 
    for(int i=2;i<=n;i++){
    	//每行第1个和最后一个数
    	a[i][1] = a[i][i] = 1;
    	//使用循环计算第i行第2个～倒数第二个数 
    	for(int j=2;j<i;j++){
    		a[i][j] = a[i-1][j-1] + a[i-1][j];
		}
	}
	
	//输出保存在二维数组a中的结果 
	for(int i=1;i<=n;i++){
		for(int j=1;j<=i;j++){
			cout<<a[i][j]<<" ";
		}
		cout<<endl;
	}
    return 0; 
}

其实每行第1个和最后一个数的计算也能放到内层循环中，原因通过下图分析可知：

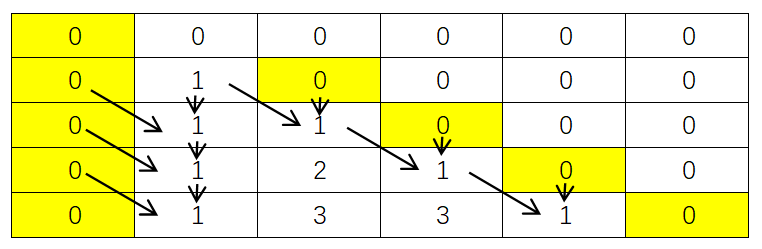
因为a[i-1][0]是0，所以a[i][1] = a[i-1][0]+a[i-1][1]也能用来计算a[i][1]；同样的，因为a[i-1][i]是0，所以a[i][i] = a[i-1][i-1]+a[i-1][i]也能用来计算a[i][i]。上面的程序可以精简为：

#include<iostream>
using namespace std;
int a[21][21];
int main()
{
	int n;
	cin>>n;
	 
    a[1][1] = 1;	//第1行
	//使用循环计算第2～n行 
    for(int i=2;i<=n;i++){
    	//使用循环计算第i行每个数 
    	for(int j=1;j<=i;j++){
    		a[i][j] = a[i-1][j-1] + a[i-1][j];
		}
	}
	
	//输出保存在二维数组a中的结果 
	for(int i=1;i<=n;i++){
		for(int j=1;j<=i;j++){
			cout<<a[i][j]<<" ";
		}
		cout<<endl;
	}
    return 0; 
}

再来看例题：T137077 杨辉三角

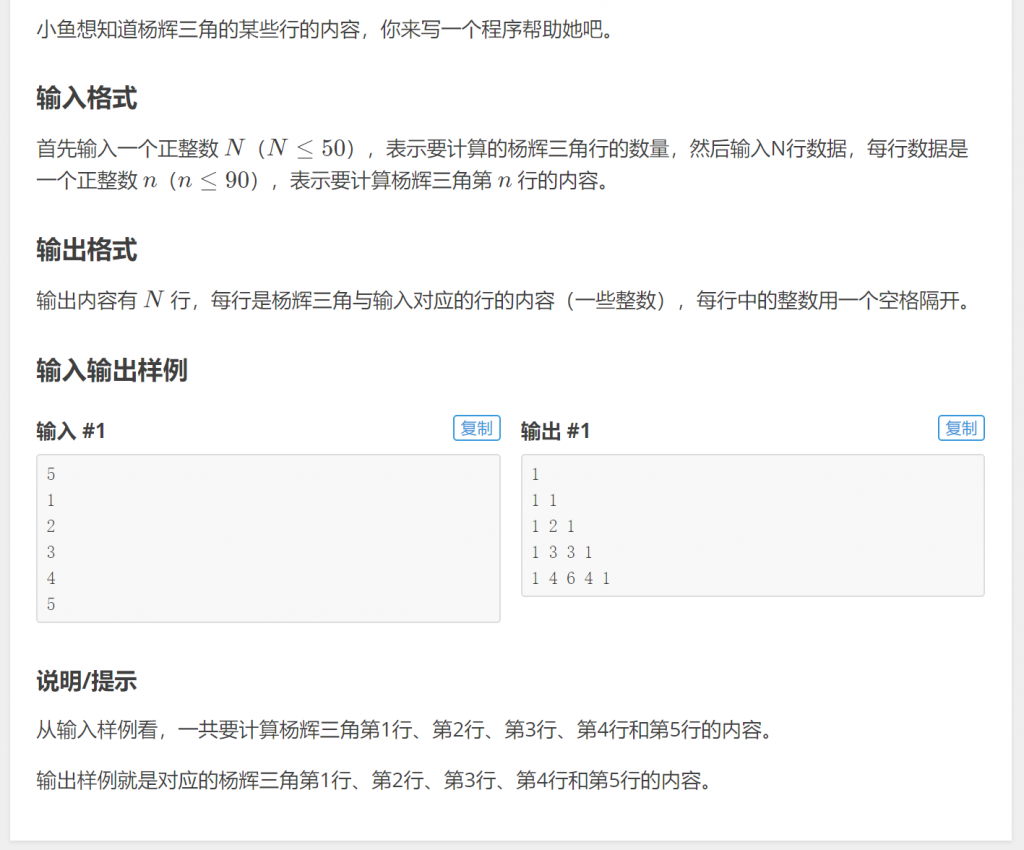
不少同学马上想到的是模拟整个过程：

#include<iostream>
using namespace std;
long long a[91][91];   //long long 
int main()
{
	int N,n;
	cin>>N;
	while(N--){         //N次循环
		cin>>n;
		
		a[1][1] = 1;    //第1行
	    //使用循环计算第2～n行 
	    for(int i=2;i<=n;i++){
	        //使用循环计算第i行每个数 
	        for(int j=1;j<=i;j++){
	            a[i][j] = a[i-1][j-1] + a[i-1][j];
	        }
	    }
	    
	    //输出第n行 
	    for(int i=1;i<=n;i++){
	    	cout<<a[n][i]<<" ";
		}
		cout<<endl;
	} 
    return 0; 
}

这样做算法时间复杂度是\(O(n^3)\)，并且出现了大量重复的计算：就拿测试样例来说，第1次计算第1行，第2次计算第2行，第3次计算第3行，第4次计算第4行，第5次计算第5行，每次计算都是从第1行到要求输出的行，出现了大量重复的计算。怎么来避免重复计算呢？

可以先输入所有要计算的行存储在数组b中，并求出最大值\(max\)，那么只需要用一个双重循环计算杨辉三角的第1～\(max\)行即可，计算完成后，杨辉三角的第1～\(max\)行都已经计算出来保存到二维数组a中了，那么根据数组b中的元素输出二维数组a中对应行的元素即可，这样做可以将算法时间复杂度降低到是\(O(n^2)\)：

#include<iostream>
using namespace std;
const int MAX = 91; 
long long a[MAX][MAX];
int b[MAX];
int main(){
	int N,max = 0;
	cin>>N;
	
	//计算出要输出的所有行编号的最大值为max 
	for(int i=1;i<=N;i++){
		cin>>b[i];		//行编号保存到数组b中 
		if(b[i]>max) max = b[i];
	}
	
	//计算杨辉三角的1～max行 
	a[1][1] = 1;
	for(int i=2;i<=max;i++){   //从第2行起开始计算每一行的数据
		for(int j=1;j<=i;j++) a[i][j] = a[i-1][j-1]+a[i-1][j];
	}
	
	//打印杨辉三角要输出的行（要输出的行编号在数组b里存储） 
	for(int i=1;i<=N;i++){
		//b[i]是要输出的行编号，这一行一共有b[i]个整数 
		for(int j=1;j<=b[i];j++) cout<<a[b[i]][j]<<" ";
		//注意体会上面的 a[b[i]][j]。相当于 int n = b[i];cout<<a[n][j]<<" "; 
		cout<<endl;
	}
	return 0;
} 

其实还可以在处理输入的每一个行数的过程中，“动态地”生成杨辉三角：

#include<iostream>
using namespace std;
const int MAX = 91;
long long a[MAX][MAX];
int main()
{
	a[1][1] = 1;
	int n,m,line = 1;	//line记录杨辉三角计算到第几行了 
	cin>>n;
	for(int k=1;k<=n;k++){
		cin>>m;
		if(m>line){		//要输出的行数m>line，表明第m行还没有计算过
			//依次计算杨辉三角的第(line+1)行到第m行 
			for(int i=line+1;i<=m;i++){
				for(int j=1;j<=i;j++){
					a[i][j] = a[i-1][j-1]+a[i-1][j];
				}
			}
			//已经计算到了第m行，更新line 
			line = m;
		}
		//输出杨辉三角第m行内容 
		for(int j=1;j<=m;j++) cout<<a[m][j]<<" ";
		cout<<endl;
	}
	return 0;
}

兴趣扩展：杨辉三角形与二项展开式系数的关系

二项展开式

\((x+y)^n = C_0x^n+C_1x^{n-1}y+C_2x^{n-2}y^2+...+C_ix^{n-i}y^i+...+C_{n-1}xy^{n-1}+C_ny^n\)

等式右边的常数\(C_0,C_1,C_2,...,C_i,...,C_{n-1},C_n\)称为二项式系数，这些常数正好是上述杨辉三角第\(n+1\)行的内容（如果杨辉三角行数从0开始计数，那么正好是杨辉三角第\(n\)行的内容）。

\((x+y)^0=1\)
\((x+y)^1=x+y\)
\((x+y)^2=x^2+2xy+y^2\)
\((x+y)^3=x^3+3x^2y+3xy^2+y^3\)
\((x+y)^4=x^4+4x^3y+6x^2y^2+4xy^3+y^4\)
\((x+y)^5=x^5+5x^4y+10x^3y^2+10x^2y^3+5xy^4+y^5\)