给定一个\(n \times n\)的方阵,从右上角开始,依次用1、2、3、…按照蛇形填充方阵的每个方格。以\(n=3,4,5\)为例,填充结果如下:
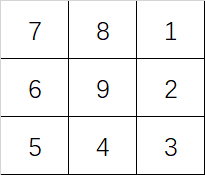
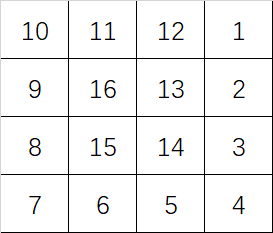
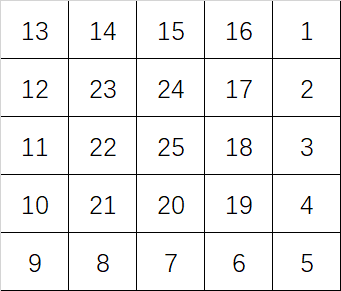
输入正整数\(n\)(\(1 \le n \le 9\)),输出\(n \times n\)方阵蛇形填充结果。
分析:要通过找规律的方式得出阵列第\(x\)行第\(y\)列的值太困难,可以通过模拟蛇形填充的过程将阵列每个方格的数填充上,当然需要将阵列中的数存储到二维数组中。
一共需要将1~\(n \times n\)一共\(n^2\)个整数填充到二维数组中,所以循环的条件不难得出。填充由坐标点\((1,n)\)开始,下一个坐标点应该由当前坐标点推导出来,填充的数字用计数器记录。
再来细看蛇形填充的过程,填充过程是有规律地重复,最基本的一个轮次是“向下填写→向左填充→向上填充→向右填充”,剩下的都是这样的重复过程,只不过最后一个轮次可能不是完整的四个方向填充都有。
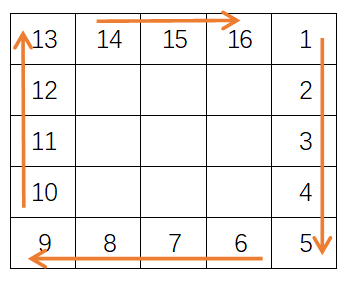
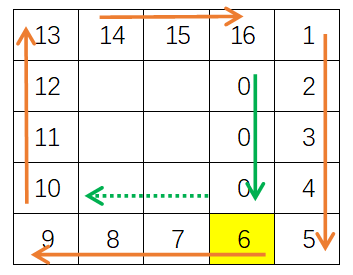
那么朝一个方向持续填充的条件是什么呢?首先想到的是填充的方格的个数,但是分析发现个数的上限并不好找,并且在同一轮次四个方向填充的个数可能都不同。我们先不看第一轮次四个方向的填充,考查第二轮次的填充,以向下填充为例,如下图所示,填充的条件是填充方向上遇到的方格的值是默认值0,只要遇到了非0值(表示这个格子之前已经填充过),那么就要“拐弯”向另一个方向填充了:
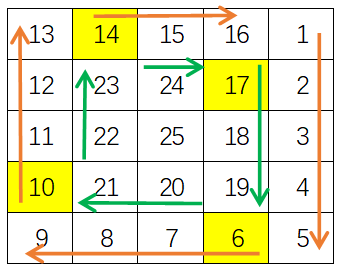
可知从第二轮次开始都是这样的填充规则,只有最外面的第一轮次不满足(其实是第一轮次的前三个方向不满足),但是我们可以人为设置三个关键点的值来让第一轮次的填充也满足填充规则:
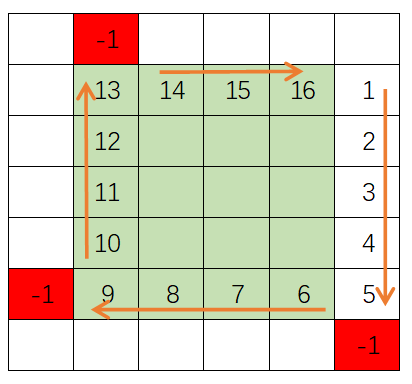
经过上面的分析:可以得出参考程序代码:
#include<cstdio>
const int N = 9;
int a[N+2][N+2]; //思考为什么不是N+1?
int main()
{
int n;
scanf("%d",&n);
//标记三个特殊点的值为非0
a[n+1][n] = a[n][0] = a[0][1] = -1;
int cnt = 0; //计数器记录要填充的数
//x,y是填充点的坐标:x行y列,填充过程中一直动态记录填充点的坐标
//最开始时在第0行n列,那么进入循环首先向下填充第一个填充点正好是方阵右上角方格
int x = 0,y = n;
while(cnt<n*n){
//向下填充:注意++x和++cnt是先自加再使用变量
while(!a[x+1][y]) a[++x][y] = ++cnt; //相当于cnt++;x++;a[x][y]=cnt;
//向左填充
while(!a[x][y-1]) a[x][--y] = ++cnt;
//向上填充
while(!a[x-1][y]) a[--x][y] = ++cnt;
//向右填充
while(!a[x][y+1]) a[x][++y] = ++cnt;
}
//输出结果
for(int x=1;x<=n;x++){
for(int y=1;y<=n;y++){
printf("%2d ",a[x][y]);
}
printf("\n");
}
return 0;
}
循环体中有四个先后顺序的循环来实现四个方向的依次填充。前面分析最后一个轮次可能不是完整的四个方向的填充,程序这里也能做到,这个时候后面方向实现填充功能的while循环条件一上来循环条件就不成立。
拓展练习:
 NOIP学习小站
NOIP学习小站