数组例题——进制转换

以我们熟悉的十进制数为例，十进制数只有0、1、2、3、4、5、6、7、8、9这10个基本数字（也称为数码）。同样的，二进制数只有0、1两个数码，八进制数只有0、1、2、3、4、5、6、7这八个数码。

对于 $n$ 进制数 $m$，书写时如果某位上数字超过10，为了避免混淆，用大写字母来表示这个位上的数。A表示10、B表示11、C表示12，...，以此类推。那么十六进制数有0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F这16个数码。

一、十进制数转其他进制

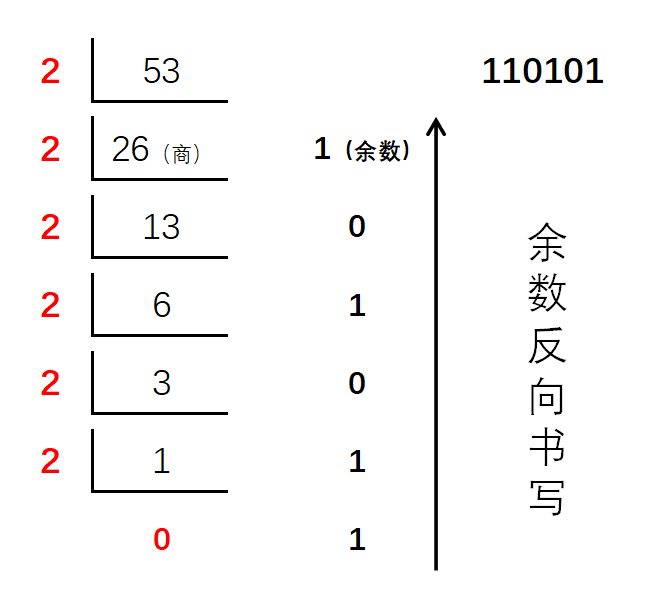
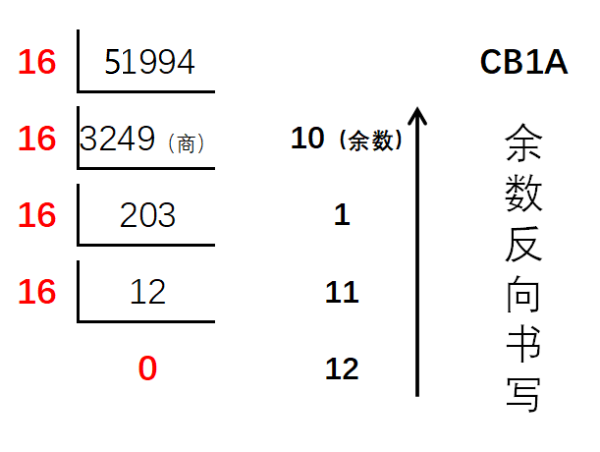
十进制数转换成其他进制可以使用短除法：

输入$m,n$（$0 \le m \le 1,000,000,2 \le n \le 16$），输出十进制数$m$转$n$进制的结果。

分析：十进制数$m$转$n$进制，依据短除法，$m$每次除以$n$，写下余数，将商重新赋值给$m$，一直重复上面的操作直到$m$为0。将所余数反向书写就是结果。可以将余数依次存入到数组中，最后逆序输出即可。

#include<iostream>
using namespace std;
//char数组s用于输出短除法的余数对应的数码
//如果余数为0，那么对应的数码是s[0]——'0'；
//如果余数为10，那么对应的数码是s[10]——'A' 
//如果余数为i，那么对应的数码是s[i]
char s[16] = {
	'0','1','2','3','4',
	'5','6','7','8','9',
	'A','B','C','D','E','F'
};
//数组r记录所有余数 
int r[1000];
int main()
{
    int m,n,cnt = 0;
    cin>>m>>n;
    
    while(m){       //while(m!=0){的简写
    	r[cnt++] = m%n;
    	m /= n;
	}
	
	if(cnt==0) r[cnt++] = 0;   //m为0特殊处理
	 
	for(int i=cnt-1;i>=0;i--){
		cout<<s[r[i]];    //注意这里的经典写法
		/*如果不理解上面的写法，可以看下面和上一句等效但简单一些的拆解写法
				int p = r[i];     //p是一个余数
				cout<<s[p]; 	  //输出p在s数组中对应的数码
				*/	 
	}
    return 0; 
}

二、其他进制数转十进制

可以使用“按权展开求和”将 $n$ 进制数转换成十进制数：

例如二进制数10101，其实是：$1 \times 2^4 + 0 \times 2^3+1 \times 2^2+0 \times 2^1+1 \times 2^0$ = 21；

又例如八进制数127，其实是：$1 \times 8^2 + 2 \times 8^1 + 7 \times 8^0$ = 87；

又例如十六进制数A1F，其实就是：$10 \times 16^2 + 1 \times 16^1 + 15 \times 16^0$ = 2591；

甚至对于十进制数12365，其实就是：$1 \times 10^4 +2 \times 10^3 +3 \times 10^2 + 6 \times 10^1 + 5 \times 10^0$ = 12365。

问题：输入正整数 $n$（$2 \le n \le 16$），以及$n$进制数$K$，输出其十进制数$m$。例如输入 16 FF，那么应该输出255。

解法一：将$n$进制数$K$按照字符的形式输入，每位是一个字符，存入到char数组中，使用按权展开求和的方法计算对应的十进制数（需要注意的是权值的处理）：

#include<iostream>
using namespace std;
char num[1010];
int main()
{
    int n,cnt = 0;
    char one;
    cin>>n;
    
    //将n进制数每位当作字符存入字符数组 
    while(cin>>one){
        num[cnt++] = one;
    }
    
    long long m = 0,p = 1;
    //按权展开求和（低位 → 高位依次处理） 
    for(int i=cnt-1;i>=0;i--){
    	if(num[i]>='0' && num[i]<='9'){
    		m += p*(num[i]-'0');
		}else if(num[i]>='A' && num[i]<='F'){
    		m += p*(10+num[i]-'A');
		}
		//处理权值p 
		p *= n;
	}
	
    cout<<m;
    return 0; 
}

解法二：可以使用while(cin>>char)的方式输入$n$进制数$K$的每一位（当作字符输入），一边输入，一边组装十进制数$m$：

#include<iostream>
using namespace std;
int main()
{
    int n;
    long long m = 0;
	char one;
	cin>>n;
	while(cin>>one){
		m = m*n;     //m放大n倍
		if(one>='0' && one<='9'){        //输入的是'0'～'9'中的某个字符
			m += one - '0';              //one-'0'就是该位数字
		}else if(one>='A' && one<='F'){  //输入的是'A'～'F'中的某个字符
			m += 10 + one - 'A';         //10+one-'A'就是该位数字
		}
	}
	cout<<m;
    return 0; 
}