递归函数

函数体中可以调用其它函数，如果一个函数题中又调用了自己，这样的函数称为递归函数。显然，函数体中不应该是无条件的递归调用，否则就和“死循环”一样的效果了。也就是在满足某些条件的时候不递归调用自身，这也就是递归函数的“出口”。

一、计算阶乘

对于阶乘，\(n! = 1 \times 2 \times ... \times (n-1) \times n\)，\((n-1)! = 1 \times 2 \times ... \times (n-1) \)，可知：

\(\begin{equation} n!=\left\{ \begin{aligned} 1\quad(n=1) \\ n \times (n-1)! \quad(n>1)\end{aligned} \right. \end{equation}\)

如果用\(f(n)\)表示\(n!\)，可知：

\(\begin{equation} f(n)=\left\{ \begin{aligned} 1\quad(n=1) \\ n \times f(n-1) \quad(n>1)\end{aligned} \right. \end{equation}\)

如果用自定义函数int f(int n);来计算并返回\(n!\)的值，那么在函数体里可以使用n*f(n-1)来作为计算结果，可见函数int f(int n);中又调用了自己，这就是递归函数：

#include<iostream>
using namespace std;
int f(int n){
	if(n==1) return 1;	//递归出口 
	return n*f(n-1);	  //递归调用自身 
}
int main()
{
	for(int i=1;i<=10;i++){
		cout<<f(i)<<endl;
	}
    return 0;
}

以main函数中i=3时，调用f(3)为例，整个调用过程如下：

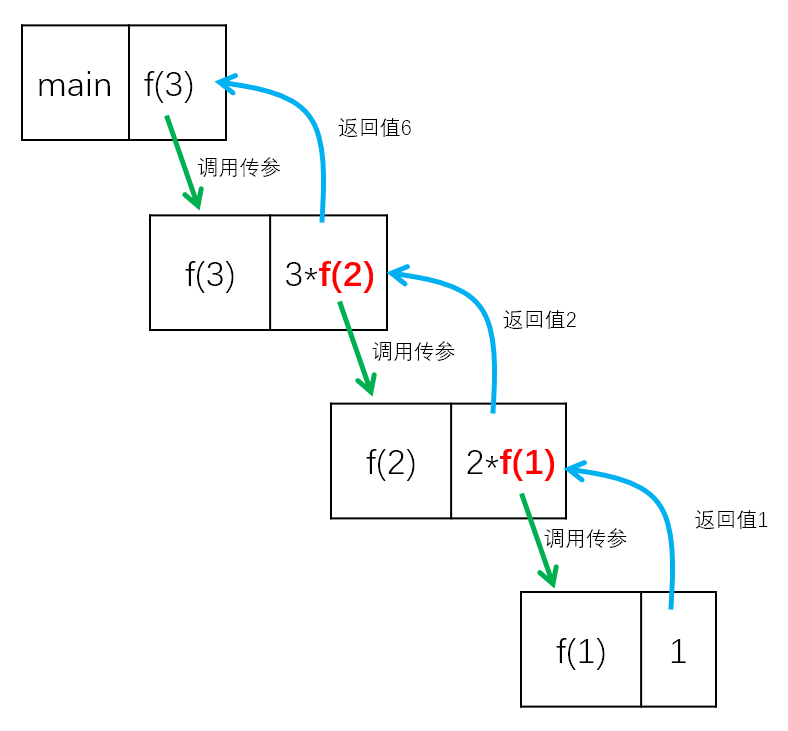
从上面分析可知，递归函数有点类似于“剥洋葱”，一层套着一层，要向下一直“剥”到最里层（也就是递归出口），然后还有向上逐层返回的过程。

二、逆序输出

再来看一个问题，输入\(n\)个整数，然后逆序输出所有的整数，我们知道在输入一个整数后需要将这个整数保存下来（当然要保存所有整数需要用到数组），等所有整数都输入完毕了，才能逆序输出：

#include<iostream>
using namespace std;
int a[1011]; 
int main(){
    int n;
    cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i];
    for(int i=n;i>=1;i--) cout<<a[i]<<" ";
    return 0;
}

其实也可以使用递归函数来实现，大家可以自行分析下面参考程序递归函数的执行过程：

#include<iostream>
using namespace std;
int n;		//n是全局变量 
//处理第k个数：输入并输出
void f(int k){
    if(k==n+1) return;	//递归出口
    int m;
    cin>>m;
    f(k+1);		//递归调用，处理第n+1个数
    cout<<m<<" ";
}
int main(){
    cin>>n;
    f(1);
    return 0;
}

#include<iostream>
using namespace std;
//输入并输出
void f(int k){
	if(k==0) return;  //递归出口
	int m;
	cin>>m;
	f(k-1);		//递归调用
	cout<<m<<" ";
}
int main(){
    int n;
    cin>>n;
    f(n);
    return 0;
}

三、斐波那契数列

前面介绍的斐波那契数列的第\(n\)项\(fib(n)\)的计算公式是：

\(\begin{equation} fib(n)=\left\{ \begin{aligned} 1\quad(n \le 2) \\ fib(n-1)+fib(n-2) \quad(n \ge 3)\end{aligned} \right. \end{equation}\)

和上面的计算阶乘一样，可以使用递归函数处理，参考程序如下：

#include<iostream>
using namespace std;
long long fib(int n){
	if(n<=2) return 1;			//递归出口 
	return fib(n-1)+fib(n-2);	 //递归调用自身（2次） 
}
int main()
{
	cout<<fib(20)<<endl;
    return 0;
}

如果调用fib(40)，会发现耗时已经接近1s了，如果调用fib(50)，耗时远远超过1s（实际测试在普通配置PC上耗时40s左右），这是什么原因呢？我们修改一下代码：

#include<iostream>
using namespace std;
long long fib(int n){
	cout<<"fib("<<n<<")"<<endl;	//通过输出额外信息来测试函数调用过程 
	if(n<=2) return 1;			 //递归出口 
	return fib(n-1)+fib(n-2);	  //递归调用自身 
}
int main()
{
	cout<<fib(6)<<endl;
    return 0;
}

在fib函数里添加上语句cout<<"fib("<<n<<")"<<endl;，那么每调用一次fib函数，就会输出fib函数“调用”信息。程序输出结果如下：

fib(6)
fib(5)
fib(4)
fib(3)
fib(2)
fib(1)
fib(2)
fib(3)
fib(2)
fib(1)
fib(4)
fib(3)
fib(2)
fib(1)
fib(2)
8

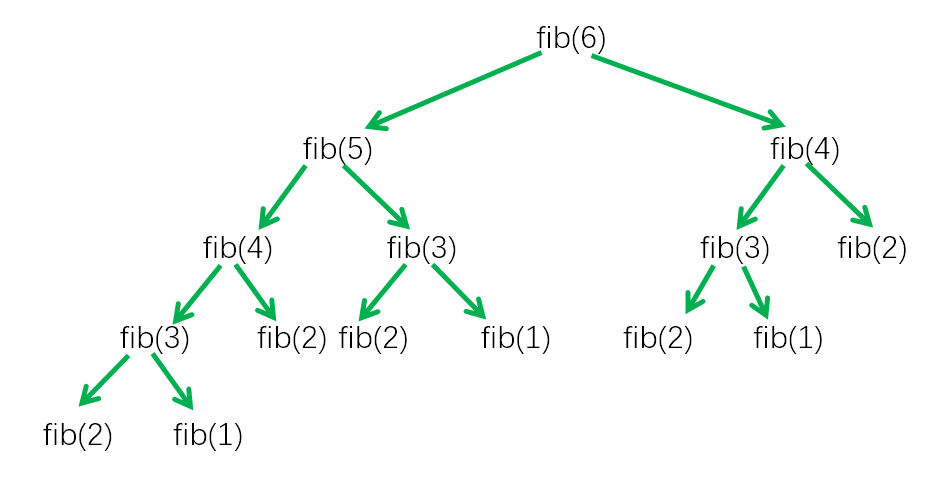
可知调用fib(6)，一共调用了2次fib(4)、3次fib(3)、5次fib(2)、3次fib(1)，其实这些调用一次就已经计算出结果了，这里出现了不必要的重复调用的情况。如果调用fib(50)，仅fib(20)就被重复调用多达1346269次，fib(4)更是被调用了2971215073次（接近30亿次）。这么多不必要的重复调用导致程序效率低下。

那么如何提高程序的运行效率呢？可以用一个全局数组a来记录计算结果，在函数体中，将fib(n)的结果保存到a[n]中，在计算前判断a[n]的值不为0的话可以直接返回a[n]（已经计算过）：

#include<iostream>
using namespace std;
long long a[51];  //全局数组用来记录fib数列每项 
long long fib(int n){
	if(a[n]) return a[n]; //已经计算过，直接返回 
	if(n<=2) return a[n] = 1;
	return a[n] = fib(n-1)+fib(n-2); 
}
int main()
{
	cout<<fib(50)<<endl;
    return 0;
}

四、辗转相除法求最大公约数

再来看辗转相除法求最大公约数，前面已经介绍了该算法的思路：

#include<iostream>
using namespace std;
int main()
{
    int m,n,r;
    cin>>m>>n;    
    do{
        r = m%n;
        m = n;
        n = r;
    }while(r!=0);
    cout<<m;   //注意这里是输出m 
    return 0;
} 

分析上面的第 3 步，其实就是计算 n 和 r（也就是 m%n）的最大公约数。可以用递归函数实现：

\(\begin{equation} gcd(m,n)=\left\{ \begin{aligned} n\quad(m\%n=0) \\ gcd(n,m\%n) \quad(m\%n \neq 0)\end{aligned} \right. \end{equation}\)

还可以简化为：

\(\begin{equation} gcd(m,n)=\left\{ \begin{aligned} m\quad(n=0) \\ gcd(n,m\%n) \quad(n>1)\end{aligned} \right. \end{equation}\)

#include<iostream>
using namespace std;
int gcd(int m,int n){
	return m%n==0?n:gcd(n,m%n);
}
int main()
{
    int x,y;
    cin>>x>>y;
    cout<<gcd(x,y)<<endl;
    return 0;
}

#include<iostream>
using namespace std;
int gcd(int m,int n){
	return n==0?m:gcd(n,m%n);
}
int main()
{
    int x,y;
    cin>>x>>y;
    cout<<gcd(x,y)<<endl;
    return 0;
}

求最大公约数还有辗转相减法：

\(\begin{equation} gcd(m,n)=\left\{ \begin{aligned} m\quad(m=n) \\ gcd(n,m) \quad(m<n)\\ gcd(n,m-n) \quad(m>n)\end{aligned} \right. \end{equation}\)

还可以对辗转相减法改良，用来高效计算高精度数（后面会介绍）的最大公约数：

【思考问题】

1.输入正整数\(m,n(m\leq3,n\leq5)\)，计算Ackmann函数的结果：

\(\begin{equation} akm(m,n)=\left\{ \begin{aligned} n+1\quad(m=0) \\ akm(m-1,1) \quad(m>0且n=0) \\ akm(m-1,akm(m,n-1)) \quad(m>0且n>0)\end{aligned} \right. \end{equation}\)

2.\(n\)条两两相交的直线将平面划分成多少个区域？注意没有任何超过2条直线相交于同一点的情况。

3.楼梯有\(n\)级台阶，上楼可以一步上一级台阶，也可以一步上两级台阶。编一程序，计算共有多少种不同的走法。