线性表——队列

中午在食堂打饭，真是一个令人头疼的事情，去食堂的路上也总是步伐匆匆，迟一点去，就会深刻领悟什么叫做人山人海了。相比较学生来说，打饭阿姨毕竟是少数，在每个窗口都有人的时候，我们就得排队等待，队列最前面的一个学生打完饭离开，后面排队的人才可以继续向前走，直到轮到自己。虽然费时，但是秩序和规则却是我们每个人都应该遵守的，也只能抱怨自己来的迟了。这里描述的就是现实生活中普遍存在的排队的情形。

一、队列的定义

用电脑的时候，有时候机器会处于疑似死机的状态，鼠标点什么似乎都没有用，双击任何快捷方式都不动，就当你快失去耐心，打算reset的时候，突然它就像酒醒了一样，把你刚才点击的所有操作全部按照顺序执行了一遍，这其实是因为操作系统中的多个程序需要通过一个通道输出，而按照先后次序排队等待造成的。

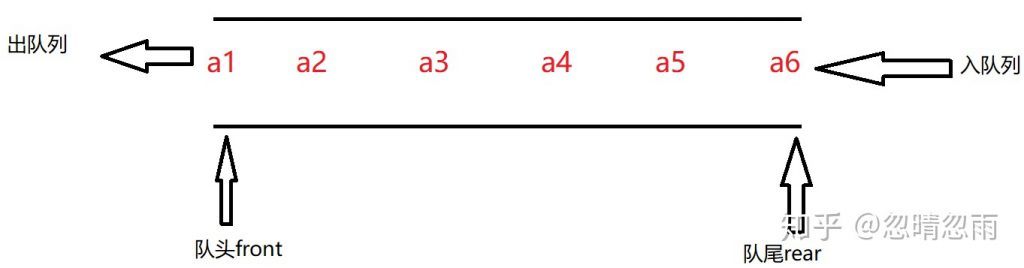
前面的例子体现出来的数据结构就是队列（queue）。队列是一种只允许在一端进行删除操作，在另一端进行插入操作的线性表。允许插入的一端称作队尾 (rear)，允许删除的的一端称为队头 (front，或者称为队首) 。队列的数据元素又叫做队列元素。在队尾插入一个队列元素称为入队，从队头删除一个队列元素称为出队 。可知队列是一种典型的先进先出 (FIFO——first in first out) 结构。

二、队列的实现

1.普通队列

同样可以使用数组来模拟队列。需要用一个“指针”来指示队头front，用另外一个“指针”来指示队尾rear。队列的操作包括入队、出队、取队首元素和判断队列是否为空等：

#include<iostream>
using namespace std;
const int MAX = 1000;

int queue[MAX];
int front = 0;	//队首“指针”，也就是队首对应数组的下标 
int rear = 0;	 //队尾“指针”，其实是下一个入队元素存放位置（真实队尾应该是rear-1）

void push(int n){	//入队（没有考虑数组已被存满无法再入队的情况） 
	queue[rear++] = n;
}
int pop(){		   //出队（没有考虑队列为空的情况） 
	return queue[front++];
}
int getfront(){	  //取队首元素（没有考虑队列为空的情况） 
	return queue[front];
}
bool empty(){	    //判断队列是否为空
	return front==rear;
} 
void print(){        //依次输出从队首到队尾的元素（测试需要）
    for(int i=front;i<rear;i++) cout<<queue[i]<<" ";
    cout<<endl;
} 
int main()
{
    for(int i=1;i<=5;i++) push(i);
	print();
	
    cout<<getfront()<<endl;    
    cout<<pop()<<endl;
    print();
    
    push(6);push(7);
    print();
    
    while(!empty()){     //全部出队
        cout<<pop()<<endl;    
    } 
    return 0;
}

2.循环队列

使用上面的方法，在入队出队的过程中，队首、队尾“指针”front和rear都在不断增大，那么很容易出现数组下标溢出的情况。并且我们还发现数组的前部（下标0～front-1）的区间被闲置了。解决问题的方法是当front和rear达到数组长度MAX的时候都重置成0，这个时候就成了循环队列：

void push(int n){	 //入队 
	queue[rear] = n;
	rear = (rear+1)%MAX;
}
int pop(){			//出队
	int t = queue[front];
	front = (front+1)%MAX;
	return t;
}

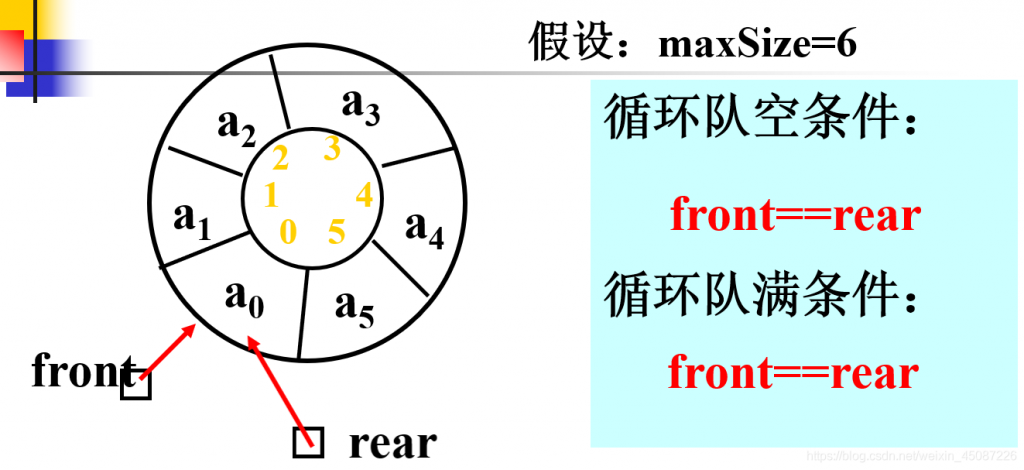
在入队和出队的过程，rear和front互相追赶，如果rear追到front说明队列满了，如果front追到rear说明队列为空。但是现在会出现一个新问题，那就是：空队特征是front == rear, 队满时也会有front == rear，可知判断条件将出现二义性。那么如何解决这个问题呢？可以设置一个标记变量flag，例如在入队时设置flag=1，出队时设置flag=0，那么结合标记变量的值就能区分开空队列和满队列的情况了：

#include<iostream>
using namespace std;
const int MAX = 6;   //设置了一个较小的循环队列容量，正好测试后面的数据

int queue[MAX];
int front = 0;	   //队首“指针”，也就是队首对应数组的下标 
int rear = 0;		//队尾“指针”，其实是下一个入队元素存放位置 
int flag = 0;	    //标记最近的操作是入队还是出队 
bool empty(){		//判断空队列 
	return flag==0 && front==rear;
}
bool full(){		 //判断满队列 
	return flag==1 && front==rear;
}
void push(int n){	//入队
	if(full()) return;	//队列满，不能再入队 
	flag = 1; 
	queue[rear] = n;
	rear = (rear+1)%MAX;
}
int pop(){			//出队
	if(empty()) return -1;	//队列空，不能出队（返回一个特殊值-1） 
	flag = 0;
	int t = queue[front];
	front = (front+1)%MAX;
	return t;
}
int getfront(){	   //取队首元素
	if(empty()) return -1;	//队列空，不能取队首元素（返回一个特殊值-1）  
	return queue[front];
}
void print(){         //依次输出从队首到队尾的元素（测试需要）
	if(empty()) return;		//空队列不处理 
	int last = rear;
	if(last<=front) last += MAX;	//rear小于front，特殊处理 
    for(int i=front;i<last;i++) cout<<queue[i%MAX]<<" ";
    cout<<endl;
}
int main()
{
    for(int i=1;i<=5;i++) push(i);
	print();
	
    cout<<getfront()<<endl;    
    cout<<pop()<<endl;
    print();
    
    push(6);push(7);
    print();
    
    while(!empty()){     //全部出队
        cout<<pop()<<endl;    
    } 
    return 0;
}

三、经典例题：使用队列解决约瑟夫问题

再来看前面介绍的约瑟夫问题，其实也可以用循环队列解决问题。开始时编号1～n依次入队；每次数到m的人出圈，其实可以认为队列里前1～m-1个人依次出队并入队，第m个人出队；如此重复操作，直到队列为空为止：

#include<iostream>
using namespace std;
const int MAX = 110;

int queue[MAX];
int front = 0;       //队首“指针”，也就是队首对应数组的下标 
int rear = 0;        //队尾“指针”，其实是下一个入队元素存放位置 
int flag = 0;        //标记最近的操作是入队还是出队 
bool empty(){        //判断空队列 
    return flag==0 && front==rear;
}
void push(int n){    //入队
    flag = 1; 
    queue[rear] = n;
    rear = (rear+1)%MAX;
}
int pop(){           //出队（返回了出队元素）
    flag = 0;
    int t = queue[front];
    front = (front+1)%MAX;
    return t;
}
int main()
{
    int n,m;
	cin>>n>>m;
	for(int i=1;i<=n;i++) push(i);
	while(!empty()){
		//队列里前m-1人依次出队并再次入队 
		for(int i=1;i<m;i++) push(pop());
		//第m个人出队 
		cout<<pop()<<" ";
	}
    return 0;
}

四、利用结构体实现循环队列

【选择阅读】也可以将队列封装成一个结构体，在结构体里使用成员函数实现队列的功能，通过调用结构体变量的成员函数实现入队、出队、判断队列是否为空：

#include<iostream>
using namespace std;

//使用结构体封装循环队列 
const int N = 10000;
struct queue{
	int pool[N];
	int front,rear,flag;
	
	queue(){	//构造函数 
		front = rear = flag = 0;
	}
	
	//判断队列是否为空 
	bool empty(){
		return flag==0 && front==rear;
	}
	
	//判断队列是否为满（存放队列元素的数组没有剩余空间） 
	bool full(){
		return flag==1 && front==rear;
	}
	
	//入队（如果队列已满，返回false）
	bool push(int n){
	    if(full()) return false; 
	    flag = 1; 
	    pool[rear] = n;
	    rear = (rear+1)%N;
	    return true;
	}
	
	//出队（如果队列为空，返回false） 
	bool pop(){
	    if(empty()) return false;
	    flag = 0;
	    front = (front+1)%N;
	    return true;
	}
	
	//取队首元素（如果队列为空，返回一个特殊值-1）
	int getfront(){
	    if(empty()) return -1;
	    return pool[front];
	}
};

void print(queue q){         //依次输出从队首到队尾的元素（测试需要）
	if(q.empty()) return;	 //空队列不处理 
	int last = q.rear;
	if(last<=q.front) last += N;	//rear小于front，特殊处理 
    for(int i=q.front;i<last;i++) cout<<q.pool[i%N]<<" ";
    cout<<endl;
}
int main()
{
	queue q;
    for(int i=1;i<=5;i++) q.push(i);
	print(q);
	
    if(!q.empty()) cout<<q.getfront()<<endl;    
    q.pop();
    print(q);
    
    q.push(6);q.push(7);
    print(q);
    
    while(!q.empty()){     //全部出队
        cout<<q.getfront()<<endl;    
    	q.pop(); 
    } 
    return 0;
}