先来看高精度正整数乘以低精度正整数的情况,直接按位相乘即可,高精度从低位到高位每位上的数字乘以低精度整数,结果每位上的数字很可能超过10,需要处理进位,并且全部计算结束后还需要考虑最后一次乘法结果的特殊进位:
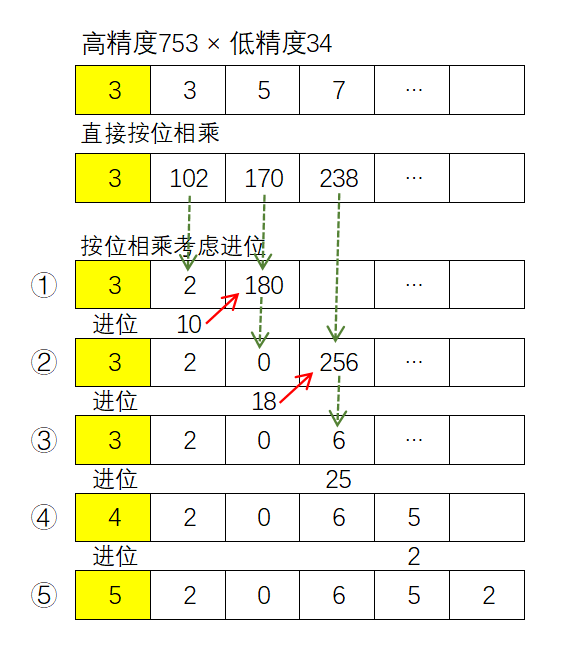
上图展示了高精度数753乘以低精度数34的处理过程,具体过程如下:
- 高精度数最低位(个位)上的数字3×34,结果为102。向高位进位10(102/10),最终结果该位只保留2(102%10);
- 高精度数下一位的数字5×34,结果为170,加上上一次计算的进位10,结果为180。向高位进位18(180/10),最终结果该位只保留0(180%10);
- 高精度数下一位的数字7×34,结果为238,加上上一次计算的进位18,结果为256。向高位进位25(256/10),最终结果该位只保留6(256%10);
- 虽然高精度数每位上的数字都做了乘法,但是由于最后一次乘法(最高位乘以低精度数)产生了进位25,所以还需要进一步处理。向高位进位2(25/10),最终结果该位只保留5(25%10);
- 向高位进位0(2/10),最终结果该位只保留2(2%10)。整个处理结束。
/* 高精度*低精度
** ma*n → mc
**/
void multi(int ma[],int n,int mc[]){
mc[0] = ma[0];
int x = 0; //进位
//按位相乘
for(int i=1;i<=ma[0];i++){
mc[i] = ma[i]*n+x;
x = mc[i]/10;
mc[i] %= 10;
}
//最高位处理后产生的进位x可能是多位数
while(x>0){
mc[++mc[0]] = x%10;
x /= 10;
}
//过滤掉高位多余的0
modify(mc);
}
/* 高精度*低精度
** ma*n → ma
**/
void multi(int ma[],int n){
int x = 0; //进位
//按位相乘
for(int i=1;i<=ma[0];i++){
ma[i] = ma[i]*n+x;
x = ma[i]/10;
ma[i] %= 10;
}
//最高位处理后产生的进位x可能是多位数
while(x>0){
ma[++ma[0]] = x%10;
x /= 10;
}
//过滤掉高位多余的0
modify(ma);
}
再来看高精度乘以高精度,通过模拟竖式运算来实现:
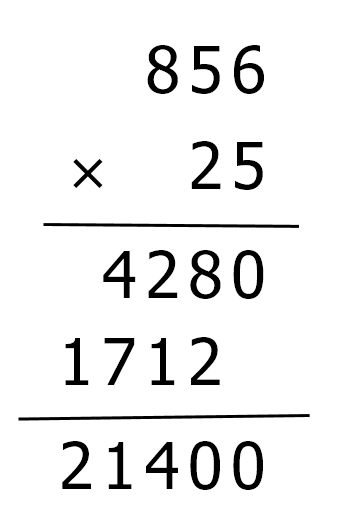
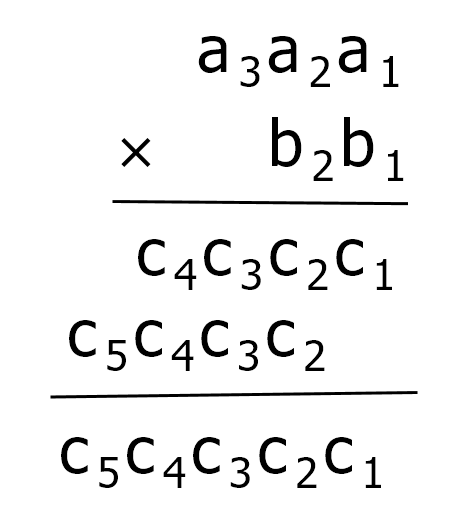
高精度数A=856,B=25,计算A×B,从竖式运算可以看出,对于B从低位到高位的每一个数字b[i],都要和A从低位到高位上的每一个数数字a[j]相乘(B个位上是5,依次和A低位到高位上的数字6、5、8相乘;同样地,B十位上的数字2,也要依次和A低位到高位上的数字6、5、8相乘),很明显,这里需要使用双重循环来实现。
将结果保存到数组c中,可知b[1]×a[1]的结果应该保存到c[1],b[1]×a[2]的结果应该保存到c[2],…;同样地b[2]×a[1]的结果也要保存到c[2],…总结规律,可知b[i]×a[j]的结果应该保存到c[i+j-1]上,并且应该是累加到c[i+j-1]上。在处理过程中,还需要考虑进位:
/* 高精度*高精度
** ma*mb → mc
**/
void multi(int ma[],int mb[],int mc[]){
memset(mc,0,N*sizeof(int)); //数组mc所有元素全部初始化为0
mc[0] = ma[0]+mb[0]; //结果位数粗略认为是ma[0]+mb[0]
for(int i=1;i<=mb[0];i++){ //对于mb的每一位
int x = 0; //记录进位
for(int j=1;j<=ma[0];j++){ //mb的每一位都要和ma的每一位相乘
mc[i+j-1] += mb[i]*ma[j]+x; //mb[i]*ma[j]放到mc[i+j-1],注意是+=
x = mc[i+j-1]/10; //计算进位
mc[i+j-1] %= 10; //修正
}
mc[i+ma[0]] = x; //考虑最高位进位
}
//过滤掉高位多余的0
modify(mc);
}
还有一种方案,就是先不考虑进位,直接使用双重循环按位相乘累加到结果中,然后再从结果的低位到高位每位都修正:
/* 高精度*高精度(另外一种解法)
** ma*mb → mc
**/
void multi2(int ma[],int mb[],int mc[]){
memset(mc,0,N*sizeof(int)); //数组mc所有元素全部初始化为0
mc[0] = ma[0]+mb[0]; //结果位数粗略认为是ma[0]+mb[0]
//直接把乘积放到mc中,不考虑进位
for(int i=1;i<=mb[0];i++){ //对于mb的每一位
for(int j=1;j<=ma[0];j++){ //mb的每一位都要和ma的每一位相乘
mc[i+j-1] += mb[i]*ma[j]; //mb[i]*ma[j]放到mc[i+j-1],注意是+=
}
}
//接下来修正每位上的数字(mc数组中有些元素很可能超过了10)
for(int i=1;i<=mc[0];i++){
mc[i+1] += mc[i]/10;
mc[i] %= 10;
}
//过滤掉高位多余的0
modify(mc);
}
完整的测试程序如下:
#include<cstdio>
#include<cstring>
#define N 10010
char s1[N],s2[N];
int a[N],b[N],c[2*N+10]; //c存放乘积,注意c数组的位数
/***********************************************************************
** 函数申明
***********************************************************************/
void convert(char s[],int arr[]); //高精度整数字符串格式化存储到数组
void print(int arr[]); //输出存储在数组中的高精度整数
void modify(int arr[]); //过滤掉高位多余的0
void multi(int ma[],int n,int mc[]); //高精度*低精度 ma*n → mc
void multi(int ma[],int n); //高精度*低精度 ma*n → ma
void multi(int ma[],int mb[],int mc[]); //高精度*高精度 ma*mb → mc
void multi2(int ma[],int mb[],int mc[]); //高精度*高精度 ma*mb → mc
/**********************************************************************/
//函数申明结束
/* 高精度正整数字符串格式化存储到数组
** arr[0]保存数字位数
** arr[1],arr[2],...,arr[arr[0]]从低位到高位依次存储高精度整数
**/
void convert(char s[],int arr[]){
memset(arr,0,N*sizeof(int)); //数组arr全部元素初始化为0
for(int i=strlen(s)-1;i>=0;i--){
arr[0]++;
arr[arr[0]] = s[i]-'0';
}
modify(arr);
}
/* 输出存储在数组中的高精度整数
**/
void print(int arr[]){
for(int i=arr[0];i>=1;i--) printf("%d",arr[i]);
}
/* 过滤掉高位多余的0
**/
void modify(int arr[]){
while(arr[arr[0]]==0 && arr[0]>1) arr[0]--;
}
/* 高精度*低精度
** ma*n → mc
**/
void multi(int ma[],int n,int mc[]){
mc[0] = ma[0];
int x = 0; //进位
//按位相乘
for(int i=1;i<=ma[0];i++){
mc[i] = ma[i]*n+x;
x = mc[i]/10;
mc[i] %= 10;
}
//最高位处理后产生的进位x可能是多位数
while(x>0){
mc[++mc[0]] = x%10;
x /= 10;
}
//过滤掉高位多余的0
modify(mc);
}
/* 高精度*低精度
** ma*n → ma
**/
void multi(int ma[],int n){
int x = 0; //进位
//按位相乘
for(int i=1;i<=ma[0];i++){
ma[i] = ma[i]*n+x;
x = ma[i]/10;
ma[i] %= 10;
}
//最高位处理后产生的进位x可能是多位数
while(x>0){
ma[++ma[0]] = x%10;
x /= 10;
}
//过滤掉高位多余的0
modify(ma);
}
/* 高精度*高精度
** ma*mb → mc
**/
void multi(int ma[],int mb[],int mc[]){
memset(mc,0,N*sizeof(int)); //数组mc所有元素全部初始化为0
mc[0] = ma[0]+mb[0]; //结果位数粗略认为是ma[0]+mb[0]
for(int i=1;i<=mb[0];i++){ //对于mb的每一位
int x = 0; //记录进位
for(int j=1;j<=ma[0];j++){ //mb的每一位都要和ma的每一位相乘
mc[i+j-1] += mb[i]*ma[j]+x; //mb[i]*ma[j]放到mc[i+j-1],注意是+=
x = mc[i+j-1]/10; //计算进位
mc[i+j-1] %= 10; //修正
}
mc[i+ma[0]] = x; //考虑最高位进位
}
//过滤掉高位多余的0
modify(mc);
}
/* 高精度*高精度(另外一种解法)
** ma*mb → mc
**/
void multi2(int ma[],int mb[],int mc[]){
memset(mc,0,N*sizeof(int)); //数组mc所有元素全部初始化为0
mc[0] = ma[0]+mb[0]; //结果位数粗略认为是ma[0]+mb[0]
//直接把乘积放到mc中,不考虑进位
for(int i=1;i<=mb[0];i++){ //对于mb的每一位
for(int j=1;j<=ma[0];j++){ //mb的每一位都要和ma的每一位相乘
mc[i+j-1] += mb[i]*ma[j]; //mb[i]*ma[j]放到mc[i+j-1],注意是+=
}
}
//接下来修正每位上的数字(mc数组中有些元素很可能超过了10)
for(int i=1;i<=mc[0];i++){
mc[i+1] += mc[i]/10;
mc[i] %= 10;
}
//过滤掉高位多余的0
modify(mc);
}
int main()
{
//将高精度正整数按照字符串的方式输入存储
scanf("%s%s",s1,s2);
//遵循存储规则,得到存储高精度正整数的数组
convert(s1,a);
convert(s2,b);
printf("输入的第1个高精度正整数是:\n");
print(a);
printf("\n\n");
printf("输入的第2个高精度正整数是:\n");
print(b);
printf("\n\n");
printf("两个高精度正整数的乘积是:\n");
multi(a,b,c);
print(c);
printf("\n\n");
printf("两个高精度正整数的乘积是:\n");
multi2(a,b,c);
print(c);
return 0;
}
那如何实现高精度自乘(ma*mb -> ma)呢?这里不能像前面高精度自加、自减那样直接修改ma的元素,可以在前面高精度乘法的基础上,最后将mc的内容复制到ma中:
/* 高精度*高精度
** ma*mb → ma
**/
void multi3(int ma[],int mb[],int mc[]){
memset(mc,0,N*sizeof(int)); //数组mc所有元素全部初始化为0
mc[0] = ma[0]+mb[0]; //结果位数粗略认为是ma[0]+mb[0]
for(int i=1;i<=mb[0];i++){ //对于mb的每一位
int x = 0; //记录进位
for(int j=1;j<=ma[0];j++){ //mb的每一位都要和ma的每一位相乘
mc[i+j-1] += mb[i]*ma[j]+x; //mb[i]*ma[j]放到mc[i+j-1],注意是+=
x = mc[i+j-1]/10; //计算进位
mc[i+j-1] %= 10; //修正
}
mc[i+ma[0]] = x; //考虑最高位进位
}
//过滤掉高位多余的0
modify(mc);
memcpy(ma,mc,N*sizeof(int)); //将结果拷贝到ma中
}
 NOIP学习小站
NOIP学习小站