先来看高精度除以低精度,观察除法竖式运算的过程:
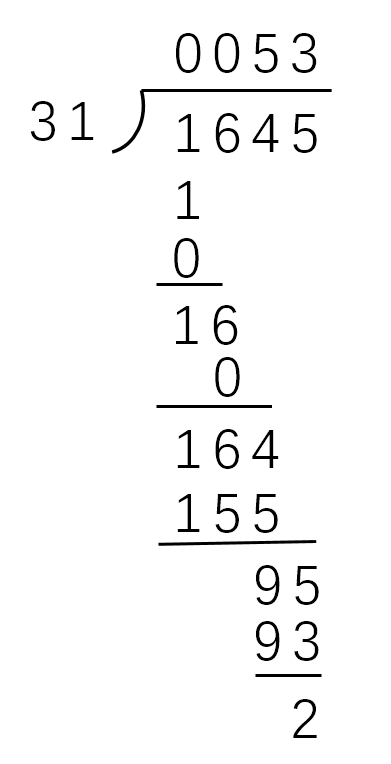
首先高精度数最高位1除以31,商0余1;然后上一次的余数1×10+高精度数的下一位6,也就是16除以31,商0余16;然后上一次的余数16×10+高精度数的下一位4,也就是164除以31,商5余9;最后上一次的余数9×10+高精度数的个位5,也就是95除以31,商3余2。所以最后的商是0053(处理后就是53),余数是2。
可知要从被除数的最高位开始,每位除以低精度数,商就是最终结果的一位,余数*10+高精度数的下一位再继续除以低精度数:
/* 高精度/低精度
** ma/n → mc,函数返回余数
** 注意要保证n!=0
**/
int div(int ma[],int n,int mc[]){
mc[0] = ma[0];
int m = 0; //m记录每次除法的余数
for(int i=ma[0];i>=1;i--){
m = m*10+ma[i];
mc[i] = m/n;
m %= n;
}
//过滤掉高位多余的0
modify(mc);
return m;
}
高精度数除以高精度数呢?其实还是模拟上面的过程,不过每次需要通过“试商法”来尝试最多可以商几(通过高精度比较和高精度自减来实现):
/* 比较高精度数ma和mb的大小
** ma>mb返回1,ma=mb返回0,ma<mb返回-1
**/
int compare(int ma[],int mb[]){
if(ma[0]>mb[0]){ //ma位数高于mb
return 1;
}else if(ma[0]==mb[0]){ //ma位数等于mb
//从高到低每位都判断
for(int i=ma[0];i>=1;i--){
if(ma[i]>mb[i]) return 1;
else if(ma[i]<mb[i]) return -1;
}
//所有位判断结束,之前没有return,那么两个高精度正整数肯定相等
return 0;
}else{ //ma位数低于mb
return -1;
}
}
/* 高精度自减
** ma-mb → ma
** 前提:ma>=mb
**/
void minus(int ma[],int mb[]){
int x = 0; //借位
//从低位到高位按位相减
for(int i=1;i<=ma[0];i++){
ma[i] = ma[i]-mb[i]-x; //从低位到高位按位相减(考虑了借位)
if(ma[i]<0){ //从高位借位
ma[i]+=10;
x = 1;
}else{ //不需要借位
x = 0;
}
}
//过滤掉高位多余的0
modify(ma);
}
/* 高精度/高精度
** ma/mb → mc,余数保存在md
** 注意要保证高精度数mb!=0
**/
void div(int ma[],int mb[],int mc[],int md[]){
mc[0] = ma[0];
md[0] = 0; //位数设置为0,后面进入循环第一次正好设置为1
for(int i=ma[0];i>=1;i--){
//以下三行通过数组后移位来组合新的“中间被除数”md
md[0]++;
for(int j=md[0];j>1;j--) md[j] = md[j-1]; //md全部后移一位,相当于*10
md[1] = ma[i]; //被除数的第i位放到md的个位上
modify(md); //修正md,避免md开始时保存的是0,处理后高位出现多余0
mc[i] = 0;
//试商法:通过比较和高精度数自减来确定商
while(compare(md,mb)>=0){ //md>=mb
minus(md,mb); //md=md-mb
mc[i]++;
}
}
//过滤掉高位多余的0
modify(mc);
}
完整的测试程序如下:
#include<cstdio>
#include<cstring>
#define N 10010
char s1[N],s2[N];
int a[N],b[N],c[N],d[N];
/***********************************************************************
** 函数申明
***********************************************************************/
void convert(char s[],int arr[]); //高精度整数字符串格式化存储到数组
void print(int arr[]); //输出存储在数组中的高精度整数
void modify(int arr[]); //过滤掉高位多余的0
int compare(int ma[],int mb[]); //比较高精度数ma和mb的大小
void minus(int ma[],int mb[]); //高精度自减 ma-mb →ma 前提:ma>=mb
int div(int ma[],int n,int mc[]); //高精度/低精度 ma/n → mc
void div(int ma[],int mb[],int mc[],int md[]); //高精度/高精度 ma/mb →mc
/**********************************************************************/
//函数申明结束
/* 高精度正整数字符串格式化存储到数组
** arr[0]保存数字位数
** arr[1],arr[2],...,arr[arr[0]]从低位到高位依次存储高精度整数
**/
void convert(char s[],int arr[]){
memset(arr,0,N*sizeof(int)); //数组arr全部元素初始化为0
for(int i=strlen(s)-1;i>=0;i--){
arr[0]++;
arr[arr[0]] = s[i]-'0';
}
modify(arr);
}
/* 输出存储在数组中的高精度整数
**/
void print(int arr[]){
for(int i=arr[0];i>=1;i--) printf("%d",arr[i]);
}
/* 过滤掉高位多余的0
**/
void modify(int arr[]){
while(arr[arr[0]]==0 && arr[0]>1) arr[0]--;
}
/* 高精度/低精度
** ma/n → mc,函数返回余数
** 注意要保证n!=0
**/
int div(int ma[],int n,int mc[]){
mc[0] = ma[0];
int m = 0; //m记录每次除法的余数
for(int i=ma[0];i>=1;i--){
m = m*10+ma[i];
mc[i] = m/n;
m %= n;
}
//过滤掉高位多余的0
modify(mc);
return m;
}
/* 比较高精度数ma和mb的大小
** ma>mb返回1,ma=mb返回0,ma<mb返回-1
**/
int compare(int ma[],int mb[]){
if(ma[0]>mb[0]){ //ma位数高于mb
return 1;
}else if(ma[0]==mb[0]){ //ma位数等于mb
//从高到低每位都判断
for(int i=ma[0];i>=1;i--){
if(ma[i]>mb[i]) return 1;
else if(ma[i]<mb[i]) return -1;
}
//所有位判断结束,之前没有return,那么两个高精度正整数肯定相等
return 0;
}else{ //ma位数低于mb
return -1;
}
}
/* 高精度自减
** ma-mb → ma
** 前提:ma>=mb
**/
void minus(int ma[],int mb[]){
int x = 0; //借位
//从低位到高位按位相减
for(int i=1;i<=ma[0];i++){
ma[i] = ma[i]-mb[i]-x; //从低位到高位按位相减(考虑了借位)
if(ma[i]<0){ //从高位借位
ma[i]+=10;
x = 1;
}else{ //不需要借位
x = 0;
}
}
//过滤掉高位多余的0
modify(ma);
}
/* 高精度/高精度
** ma/mb → mc,余数保存在md
** 注意要保证高精度数mb!=0
**/
void div(int ma[],int mb[],int mc[],int md[]){
mc[0] = ma[0];
md[0] = 0;
for(int i=ma[0];i>=1;i--){
//以下三行通过数组后移位来组合新的“中间被除数”md
md[0]++;
for(int j=md[0];j>1;j--) md[j] = md[j-1]; //md全部后移一位,相当于*10
md[1] = ma[i]; //被除数的第i位放到md的个位上
modify(md); //修正md,避免md开始时保存的是0,处理后高位出现多余0
mc[i] = 0;
//试商法:通过比较和高精度数自减来确定商
while(compare(md,mb)>=0){ //md>=mb
minus(md,mb); //md=md-mb
mc[i]++;
}
}
//过滤掉高位多余的0
modify(mc);
modify(md);
}
int main()
{
//将高精度正整数按照字符串的方式输入存储
scanf("%s%s",s1,s2);
//遵循存储规则,得到存储高精度正整数的数组
convert(s1,a);
convert(s2,b);
printf("输入的第1个高精度正整数是:\n");
print(a);
printf("\n\n");
printf("输入的第2个高精度正整数是:\n");
print(b);
printf("\n\n");
div(a,b,c,d);
printf("两个高精度正整数的商是:\n");
print(c);
printf("\n\n两个高精度正整数的余数是:\n");
print(d);
return 0;
}
如果高精度数除以高精度数,结果保留n位小数,该如何处理呢?其实可以在上面的高精度数除以高精度数的基础上再进一步处理:
/* 高精度/高精度,保留n位小数(四舍五入)
** ma/mb → mc,小数部分保留在me
** 注意要保证高精度数mb!=0
**如果在n位小数内能够被除尽,返回true,否则返回false
**/
bool div(int ma[],int mb[],int mc[],int md[],int me[],int n){
mc[0] = ma[0];
md[0] = 0;
for(int i=ma[0];i>=1;i--){
//以下三行通过数组后移位来组合新的“中间被除数”md
md[0]++;
for(int j=md[0];j>1;j--) md[j] = md[j-1];
md[1] = ma[i];
modify(md);
mc[i] = 0;
//通过比较和高精度数自减来确定商
while(compare(md,mb)>=0){ //md>=mb
minus(md,mb); //md=md-mb
mc[i]++;
}
}
//过滤掉高位多余的0
modify(mc);
//上面部分与高精度/高精度一致,接下来计算小数部分
me[0] = 0; //如果结果是整数(被整除),那么返回值是true,并且me[0]==0
if(md[0]==1 && md[1]==0) return true; //被整除(md==0)
//小数部分(一共计算n+1位小数)
for(int i=1;i<=n+1;i++){
//以下三行通过数组后移位来组合新的“中间被除数”md
md[0]++;
for(int j=md[0];j>1;j--) md[j] = md[j-1];
md[1] = 0;
me[0]++;
me[i] = 0;
//通过比较和高精度数自减来确定商
while(compare(md,mb)>=0){ //md>=mb
minus(md,mb); //md=md-mb
me[i]++;
}
if(md[0]==1 && md[1]==0) break; //余数为0,提前结束
}
if(me[0]<=n) return true; //n位小数内被除尽
//保留n位小数(第n+1位小数不小于5则要向上进位)
int x = me[me[0]]>=5?1:0;
for(int i=me[0]-1;i>=1 && x;i--){
me[i]++;
if(me[i]==10) me[i]-=10,x=1;
else x=0;
}
me[0]--;
//向整数进位(小数进位结束后如果x==1那么需要向整数个位进位1)
for(int i=1;i<=mc[0] && x;i++){
mc[i]++;
if(mc[i]==10) mc[i]-=10,x=1;
else x=0;
}
if(x) mc[++mc[0]] = x;
return false;
}
 NOIP学习小站
NOIP学习小站