计数排序

一、计数排序

先来看一个例题“P1271 选举学生会”：

学校正在选举学生会成员，有 \(n\)（\(n \le 999\)）名候选人，每名候选人编号分别从 1 到  \(n\)，现在收集到了  \(m\)（ \(m \le 2000000\)） 张选票，每张选票都写了一个候选人编号。现在想把这些堆积如山的选票按照投票数字从小到大排序。输入 \(n\) 和 \(m\) 以及 \(m\) 张选票上的数字，求出排序后的选票编号。

如果开一个最大规模的数组int a[2000000];来存储每张选票的编号，对数组进行排序，那么当实际选票数量\(m\)很大的时候肯定会出现超时。

其实将所有选票都投入到同一个票箱里，后面统计工作效率会很低下。如果设置\(n\)个票箱（每个候选人对应一个票箱），投票时支持哪一位候选人就将票投到这个候选人的票箱里，后面要统计候选人的得票数直接数他的票箱里票数即可，这样做大大提高了效率（虽然实际操作时为了保护投票人的隐私不会这样做）。那么我们在编写程序时可以用这样的方案去记录每一位候选人的得票数，最后根据得票数恢复成题目要求的“排序后的选票编号”，这样做就能不排序而得出排序结果，比起排序程序的执行效率会大大提高：

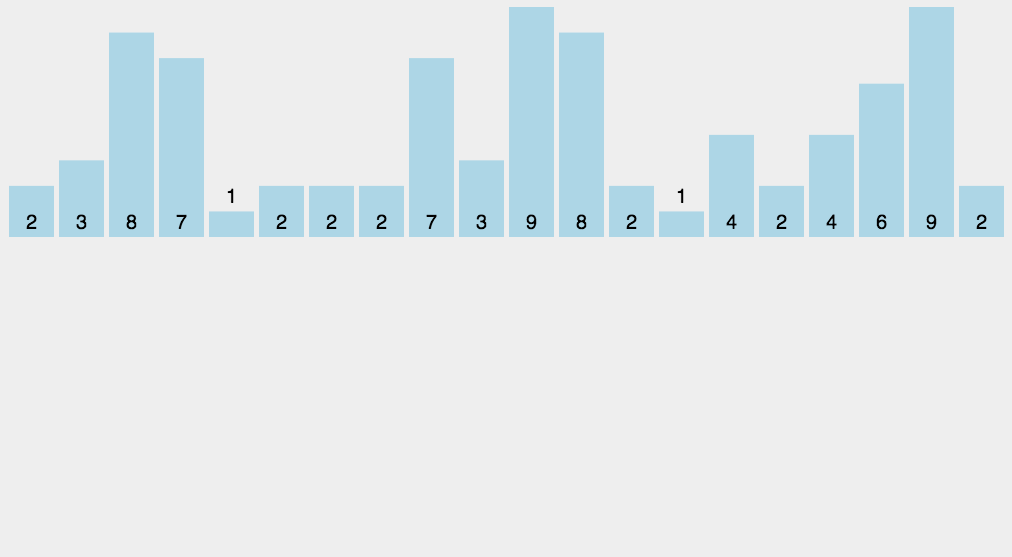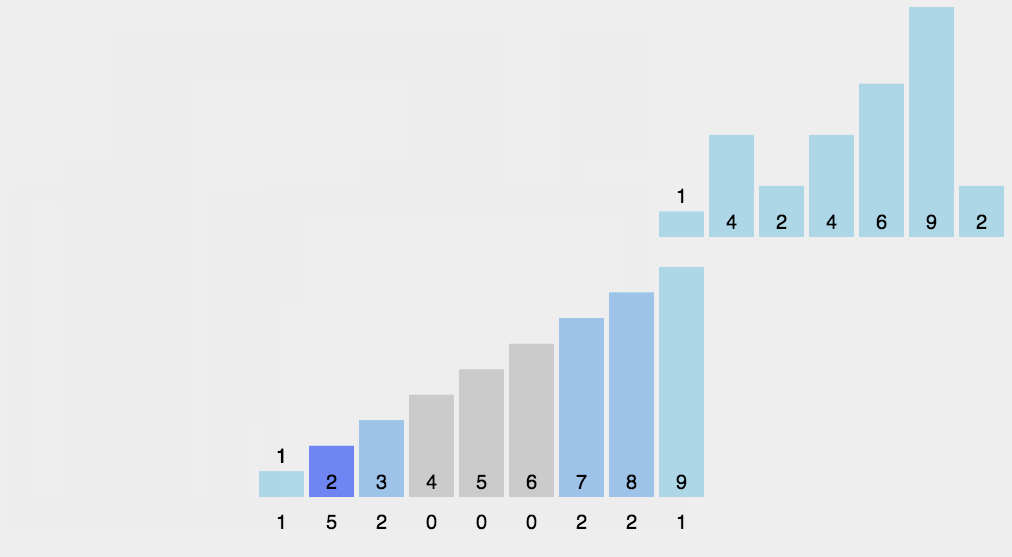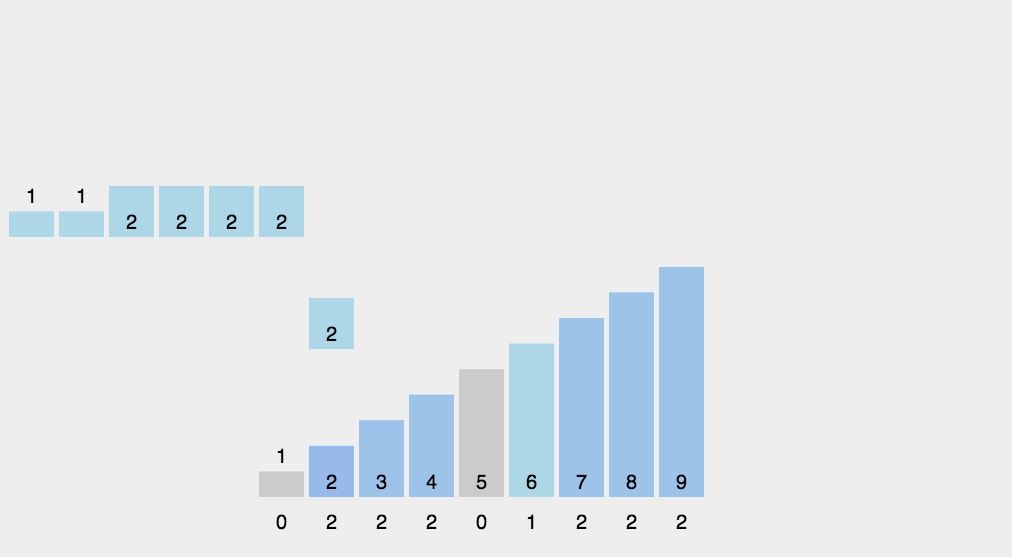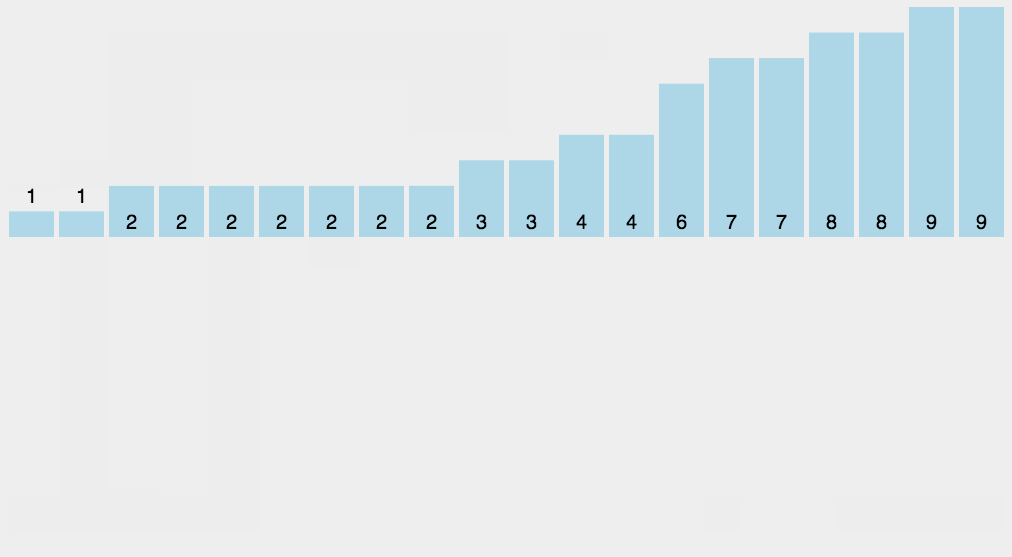
#include<iostream>
using namespace std;
int a[1000];       //候选人i的得票数记录在a[i]中
int main(){ 
	int n,m,t;
	cin>>n>>m;

	//根据每张选票统计每个候选人的得票数
	for(int i=1;i<=m;i++){
		cin>>t;    //投给了候选人t
		a[t]++;    //候选人t得票数+1
	}

	//清查每一个候选人的得票数，输出题目要求的“排序后的选票编号”
	for(int i=1;i<=n;i++){
		//候选人i的得票数记录在a[i]中，也就是i一共出现了a[i]次，输出a[i]次i 
		for(int j=1;j<=a[i];j++) cout<<i<<" ";
	}
	return 0;
} 

只需要开一个不小于\(n\)的数组用来统计每位候选人的选票，至于每张选票上的编号，都不用全部记录下来，整个过程也没有真正的去排序。

像这样的排序方法称为“计数排序”。可知计数排序的时间复杂度是\(O(n)\)。但是计数排序有一个前提，就是要排序的数据都集中在一个范围内，并且这个范围是不大的（如果范围大到千万上亿，要开这样的大数组都不现实）。

计数排序的思想是很实用的，我们再来看一个例题：P1598 垂直柱状图

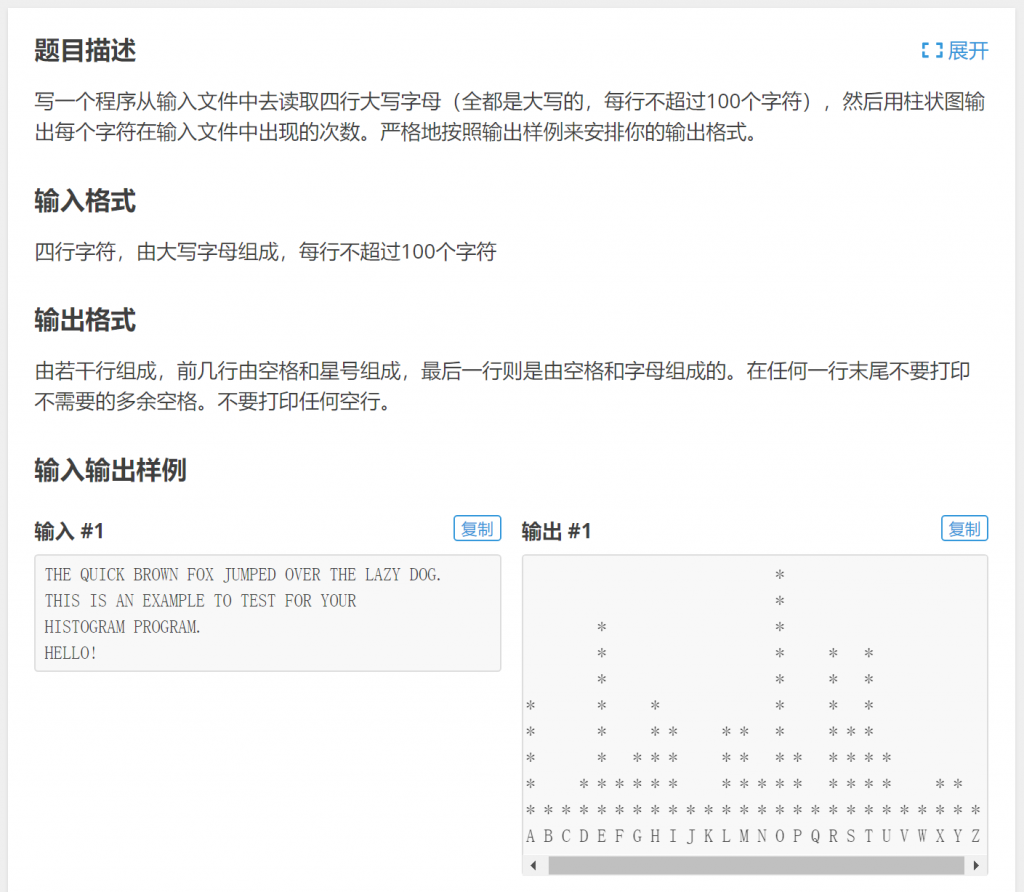
这个问题有两个难点，第一个是“统计图”原始数据如何产生，第二个是如何生成“统计图”。我们这里只研究第一个——“统计图”原始数据如何产生。

要统计一段话里每个字符的出现次数，我们只关心这段话里每个大写字母的出现次数，很明显，和上面的计数排序一样，可以用int数组a来统计从'A'到'Z'每个大写字母出现的次数，将'A'出现次数记录到a[0]中、'B'出现次数记录到a[1]中、……'Z'出现次数记录到a[25]中：

#include<iostream>
using namespace std;
char str[110];
int tot[26];
int main()
{
	while(cin>>str){
		int i = 0;
		while(str[i]!='\0'){
			if(str[i]>='A' && str[i]<='Z') tot[str[i]-'A']++;
			i++;
		}
	}
	return 0;
} 

二、排序并去重

再来看一个“排序并去重”的例题，P1059 明明的随机数：

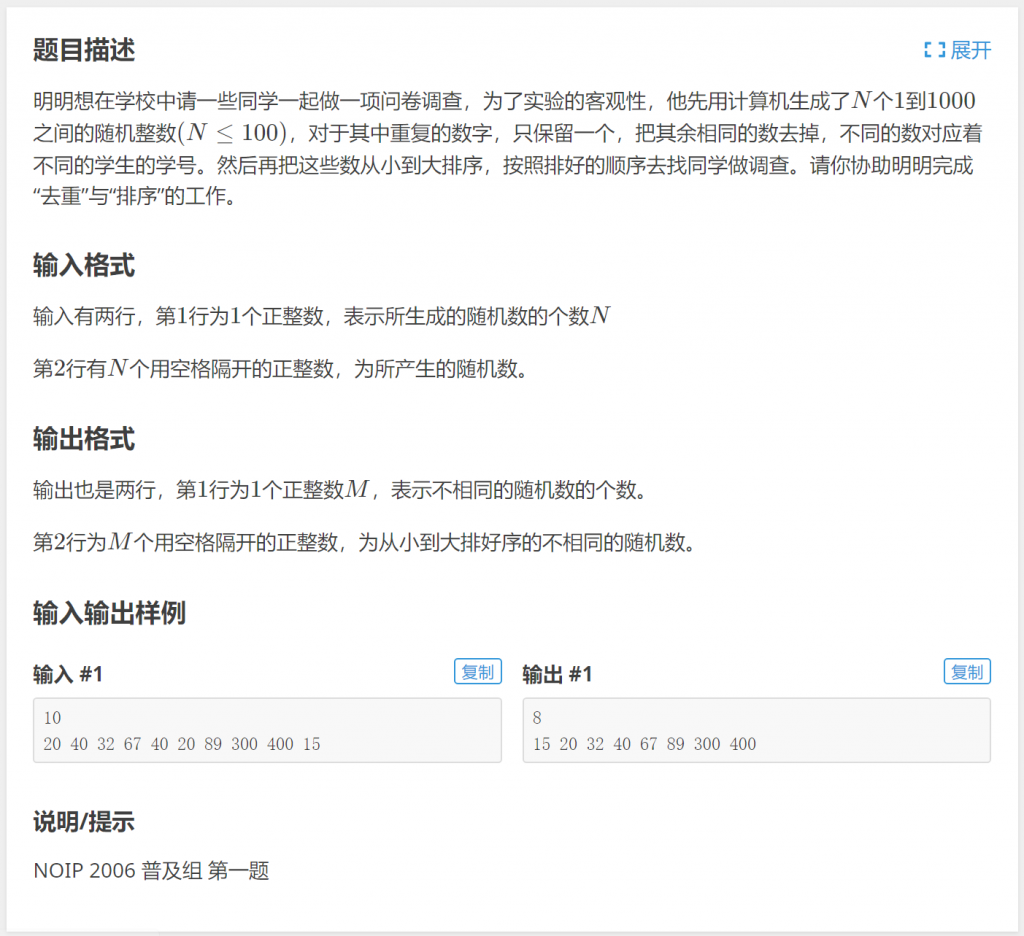
解法一：借助计数排序的思想很容易就能实现，输入一个整数就将该整数出现的次数+1。完成每个数字的计数后，遍历1～1000的每个整数，如果发现其出现次数大于0，那么去重后的整数数量+1，从而得出去重后整数数量；再次遍历1～1000的每个整数，如果发现其出现次数大于0，输出这个整数。

#include<iostream>
using namespace std;
const int MAXN = 1000;
int a[MAXN+10];
int main()
{
	int n,m;
	cin>>n;
	while(n--){
		cin>>m;
		a[m]++;
	}

	int tot = 0;
	for(int i=1;i<=MAXN;i++){
		if(a[i]) ++tot;
	}
	cout<<tot<<endl;

	for(int i=1;i<=MAXN;i++){
		if(a[i]) cout<<i<<" ";
	}
	return 0;
} 

解法二：因为最多只有100个数字，可以直接存储到数组中使用sort函数排序，排序结束后再次扫描数组每个元素，生成去重后的新数组：

#include<iostream>
#include<algorithm>
using namespace std;
const int N = 100;
int a[N],ans[N];
int main()
{
    int n,m;
    cin>>n;
    for(int i=0;i<n;i++) cin>>a[i];
    sort(a,a+n);
    
    ans[0] = a[0];
    int cnt = 1;
    for(int i=1;i<n;i++){
        if(a[i]!=a[i-1]) ans[cnt++] = a[i]; 
    }

    cout<<cnt<<endl;
    for(int i=0;i<cnt;i++) cout<<ans[i]<<" ";
    return 0;
}

解法三：仍然是先排序，排序后使用unique函数去重。unique函数的用法是unique(a,a+n)，其作用是将已经有序的数组a的a[0]到a[n-1]的所有元素去重（可知两个参数和sort函数一样是指针），函数返回去重后最后一个元素的下一个元素对应的指针，那么去重后的元素的数量是unique(a,a+n)-a：

#include<iostream>
#include<algorithm>
using namespace std;
const int N = 100;
int a[N];
int main()
{
	int n,m;
	cin>>n;
	for(int i=0;i<n;i++)
		cin>>a[i];
	sort(a,a+n);

	int cnt = unique(a,a+n)-a;
	cout<<cnt<<endl;
	for(int i=0;i<cnt;i++)
		cout<<a[i]<<" ";
	return 0;
} 

#include<iostream>
#include<algorithm>
using namespace std;
const int N = 100;
int a[N];
int main()
{
	int n,m;
	cin>>n;
	for(int i=0;i<n;i++)
		cin>>a[i];
	sort(a,a+n);
	int *end = unique(a,a+n);
	int cnt = end-a;
	cout<<cnt<<endl;
	for(int *p=a;p!=end;p++)
		cout<<*p<<" ";
	return 0;
} 

这里的unique函数也可以自己实现：

#include<iostream>
#include<algorithm>
using namespace std;
const int N = 100;
int a[N];
//自己实现简单版unique函数，对已经升序排序的begin~end去重（不包含end） 
int* unique(int *begin,int *end){
	int *q = begin+1;
	for(int *p=begin+1;p!=end;p++){
		if(*p != *(p-1)) *(q++) = *p;
	}
	return q;
}
int main()
{
    int n,m;
    cin>>n;
    for(int i=0;i<n;i++)
        cin>>a[i];
    sort(a,a+n);
    int *end = unique(a,a+n);
    int cnt = end-a;
    cout<<cnt<<endl;
    for(int *p=a;p!=end;p++)
        cout<<*p<<" ";
    return 0;
} 

其他解法：后面会学习STL（标准模板库）的集合set和字典map容器，最简单的方法是使用set或者map容器来自动实现排序并去重。