快速排序

一、快速排序

从快速排序（Quick Sort）的名称来看就知道这种排序的效率要高于前面介绍的选择排序、插入排序和冒泡排序。快速排序的原理其实很简单，以升序排序为例，首先在序列里找到一个基准元素（可以随意找一个，一般用序列第一个元素或者中间的元素作为基准元素），然后将序列中比基准元素小的元素放到基准元素的左边，将序列中比基准元素大的元素放到基准元素的右边；然后再对基准元素左边和右边的序列再使用这样的方法继续处理，直到发现基准元素左边（或右边）的序列只有一个元素为止。

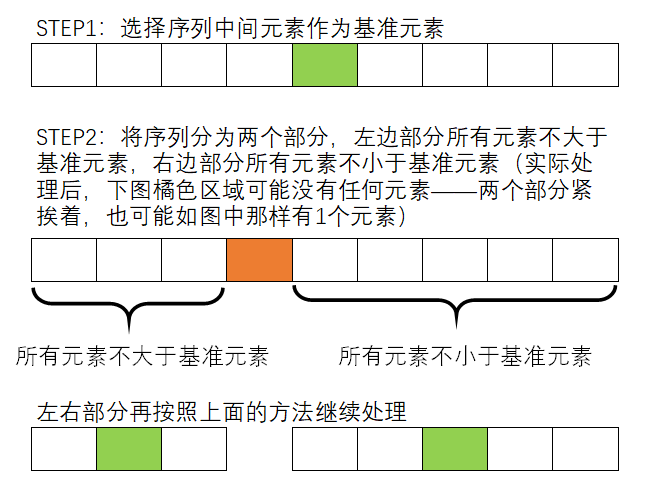
分析上面的描述过程，可知快速排序可以用递归函数实现。我们先分析第 2 步“将序列分为两个部分，左边部分所有元素不大于基准元素，右边部分所有元素不小于基准元素”如何实现。

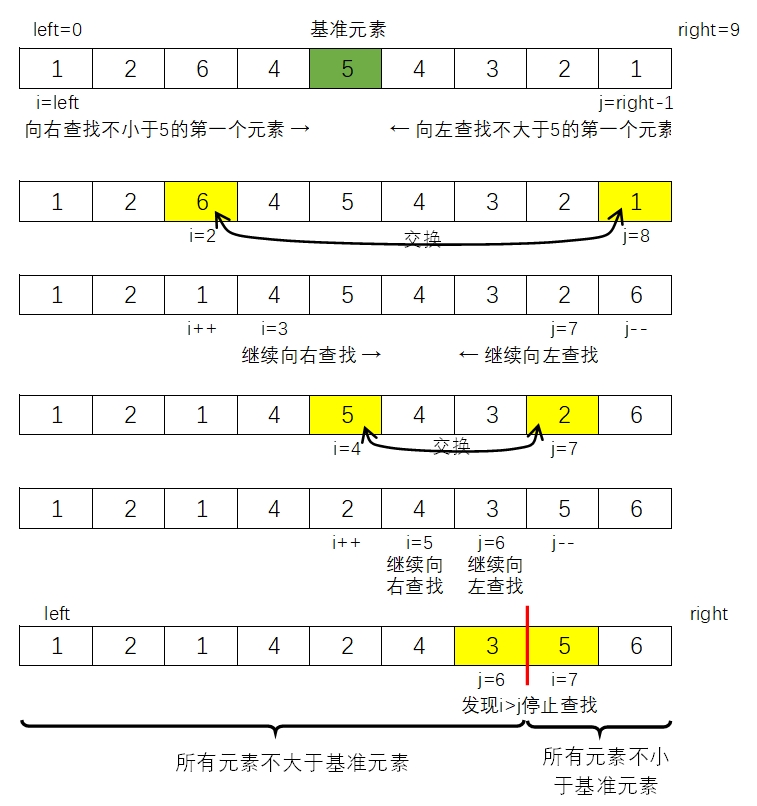
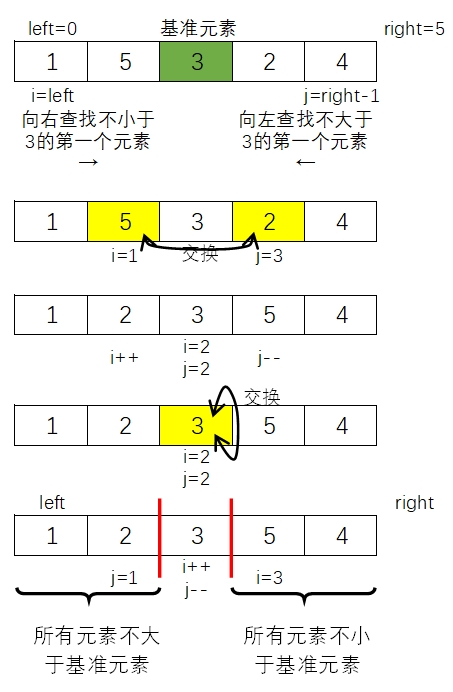
如上图所示，序列 r 排序区间为 left 下标到 right-1 下标所有元素，首先设置 i = left,j = right-1，那么基准元素可以取值为 flag = r[(i+j)/2]。

然后从序列 r[i] 元素开始向右查找不小于基准元素 flag 的第一个元素（通过 i++ 来不断向右查找），从序列 r[j] 元素开始向左查找不大于基准元素 flag 的第一个元素（通过 j-- 来不断向左查找）。

查找到后如果 i<=j，那么交换 r[i] 和 r[j]，然后 i++ 从 r[i] 右边下一个元素继续向右查找不小于基准元素 flag 的第一个元素，同样地 j-- 从 r[j] 左边前一个元素继续查找不大于基准元素 flag 第一个元素，找到后重复上面的处理过程……

整个查找处理的过程中 i 不断增大，j 不断减小，最终会出现 i>j，此时已经实现了按要求将整个序列划分成两个部分了（左边部分均不大于基准元素，右边部分均不小于基准元素）。

划分成两个部分后，左右两个部分再继续执行上面的操作即可，这里使用递归函数来实现：

//快速排序：对数组的r[left]~r[right-1]区域排序（升序排序）
void QuickSort(int r[],int left,int right){
	int i = left;
	int j = right-1;
	int flag = r[(i+j)/2];
	
	do{
		while(r[i]<flag) i++;		//左边查找第一个不小于flag的元素 
		while(flag<r[j]) j--;		//右边查找第一个不大于flag的元素
		if(i<=j){
			int t = r[i];r[i] = r[j];r[j] = t;	  //交换 
			i++;j--;								//下一个位置继续查找 
		}
	}while(i<=j);
	
	if(left<j) QuickSort(r,left,j+1);
	if(i<right-1) QuickSort(r,i,right);
}
//调用方法举例：QuickSort(a,0,10);
//调用方法举例：QuickSort(a,0,a+n);
//调用方法举例：QuickSort(a,1,a+n+1);

仿照 sort 函数的写法，用两个指针作为函数参数来指定排序的区域：

//快速排序：对指针begin~end区域排序（升序排序，不包括end）
void QuickSort(int *begin,int *end){
    int *p = begin;
    int *q = end-1;
    int flag = *(begin+(end-begin)/2);  //不能写成 *((begin+end)/2)，两个指针不能做加法
    
    do{
        while(*p < flag) p++;        //左边查找第一个不小于flag的元素 
        while(flag < *q) q--;        //右边查找第一个不大于flag的元素
        if(p<=q){
            int t = *p;*p = *q;*q = t;      //交换 
            p++;q--;                        //下一个位置继续查找 
        }
    }while(p<=q);
    
    if(begin<q) QuickSort(begin,q+1);
    if(p<end-1) QuickSort(p,end);
}
//调用方法举例：QuickSort(a,a+10);
//调用方法举例：QuickSort(a,a+n);
//调用方法举例：QuickSort(a+1,a+n+1);

快速排序的平均时间复杂度是 \(O(n\log{n})\)，最坏情况是 \(O(n^2)\)。从排序的过程可以发现，每次交换的两个数在位置上可以是随意的，所以快速排序是不稳定排序。

二、第 \(k\) 小的数

再来看一个问题，求序列中第 \(k\) 小的数（洛谷P1923）。并不需要全部排序结束就能提前得知序列中第 \(k\) 小的数，如果将整个序列排序结束后再来输出第 \(k\) 小的数效率不高。

前面介绍的快速排序，一趟结束后将序列分成了三个部分：

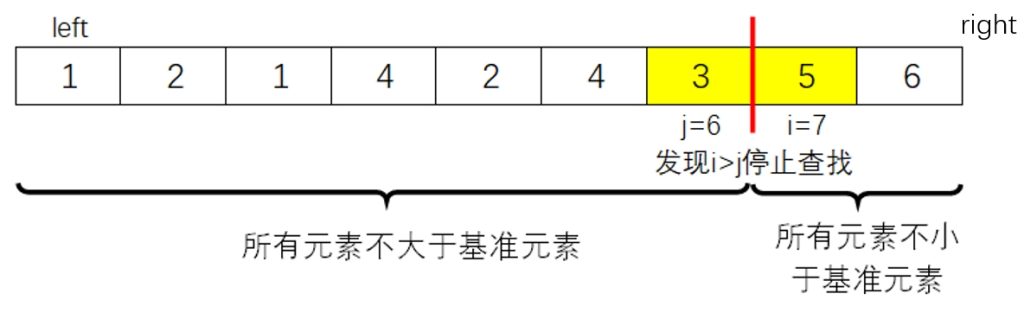
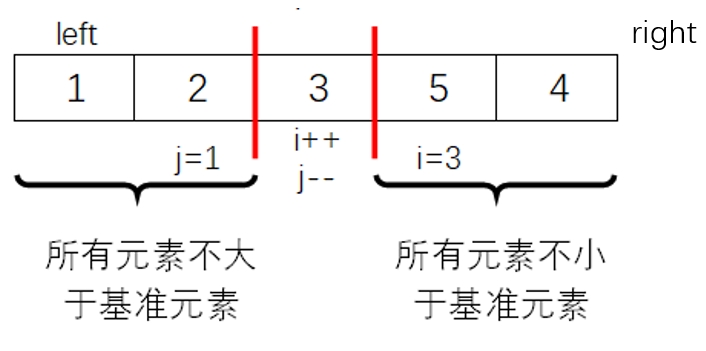
求序列中第 \(k\) 小的数（最小的数是第 0 小的数）也可以用快速排序的思想，一趟快排结束后：

1. 如果 \(k \le j\)，那么需要在 \([left,j+1)\) 区间中继续找第 \(k\) 小的数；
2. 如果 \(i \le k\)，那么需要在 \([i,right)\) 区间中继续找第 \(k\) 小的数；
3. 如果 \(j < k < i\)，那么第 \(k\) 小的数是 \(r[j+1]\)（或者 \(r[i-1]\)）。

只需要将前面的快排函数稍微改动即可：

//在数组r[left]~r[right-1]区域内查找第k小的数（最小的数是第0小的数） 
int Findkth(int r[],int left,int right,int k){
	int i = left;
	int j = right-1;
	int flag = r[(i+j)/2];

	do{
		while(r[i]<flag) i++;		//左边查找第一个不小于flag的元素 
		while(flag<r[j]) j--;		//右边查找第一个不大于flag的元素
		if(i<=j){
			int t = r[i];r[i] = r[j];r[j] = t;	  //交换 
			i++;j--;								//下一个位置继续查找 
		}
	}while(i<=j);

	if(k<=j) return Findkth(r,left,j+1,k);
	if(i<=k) return Findkth(r,i,right,k);
	return r[j+1];      //也可以retuen r[i-1];
}
//调用方法举例：Findkth(a,0,10,5);
//调用方法举例：Findkth(a,0,a+n,m);
//调用方法举例：Findkth(a,1,a+n+1,m);

在 algorithm 头文件中有一个函数 nth_element，可以用来求数组中第 \(k\) 小的数，用法很简单：nth_element(a,a+k,a+n);就能将数组 a 中 a[0]～a[n-1] 范围内所有元素中第 \(k\) 小的数存储到 a[k] 中（也是通过排序实现的，不过和前面一样排序可能还没有完全结束就能得出第 \(k\) 小的数。同样地，这里最小的数是第 0 小的数），处理后 a[k] 就是 a[0]～a[n-1] 范围内所有元素第 \(k\) 小的数。与 sort 函数一样，可以为 nth_element 函数指定比较函数，用法是：nth_element(a,a+k,a+n,cmp);。

这里的 nth_element 函数也可以自己实现：

//在针begin~end区域内查找第(target-begin)小的数（不包括end，最小的数是第0小的数）
//会将第(target-begin)小的数存储在target处
//简单版本的nth_element函数 
void nth_element(int *begin,int *target,int *end){
    int *p = begin;
    int *q = end-1;
    int flag = *(begin+(end-begin)/2);
    
    do{
        while(*p < flag) p++;        //左边查找第一个不小于flag的元素 
        while(flag < *q) q--;        //右边查找第一个不大于flag的元素
        if(p<=q){
            int t = *p;*p = *q;*q = t;      //交换 
            p++;q--;                        //下一个位置继续查找 
        }
    }while(p<=q);

    if(target<=q) nth_element(begin,target,q+1);
    else if(p<=target) nth_element(p,target,end);
}