归并排序

一、归并排序

归并排序（Merge sort），是创建在归并操作上的一种有效的排序算法，是采用分治法（Divide and Conquer）的一个非常典型的应用。归并排序思路简单，速度仅次于快速排序，且排序稳定，一般用于对总体无序，但是各子项相对有序的数列。

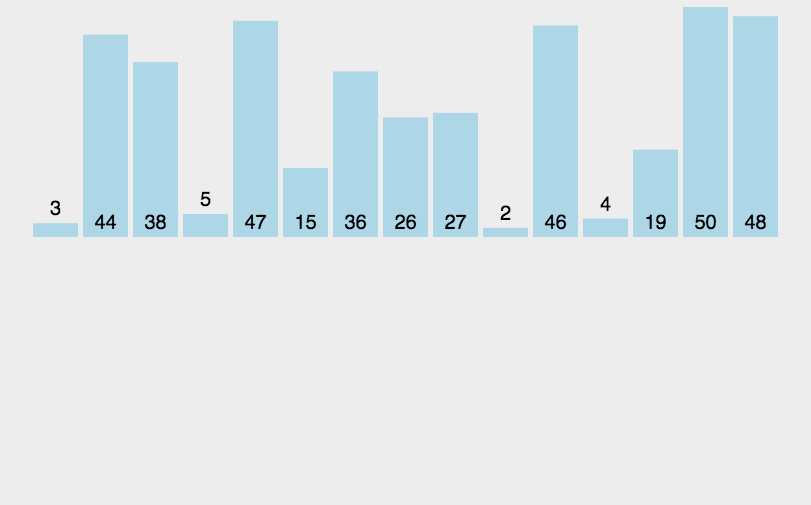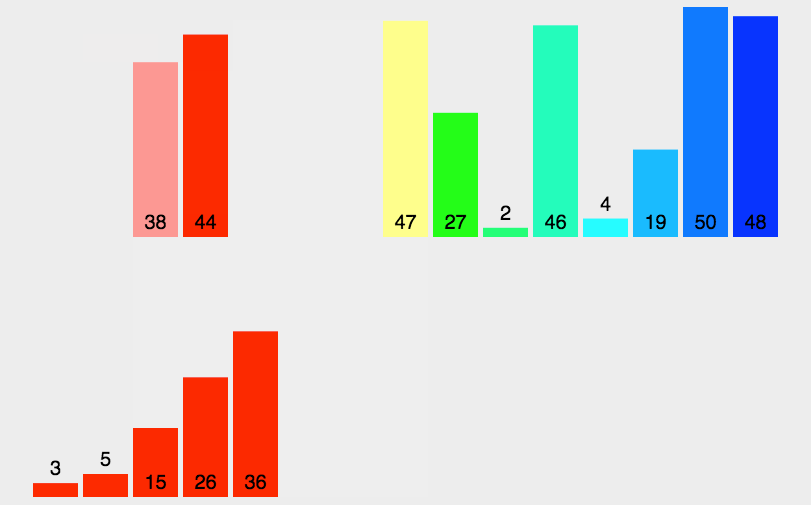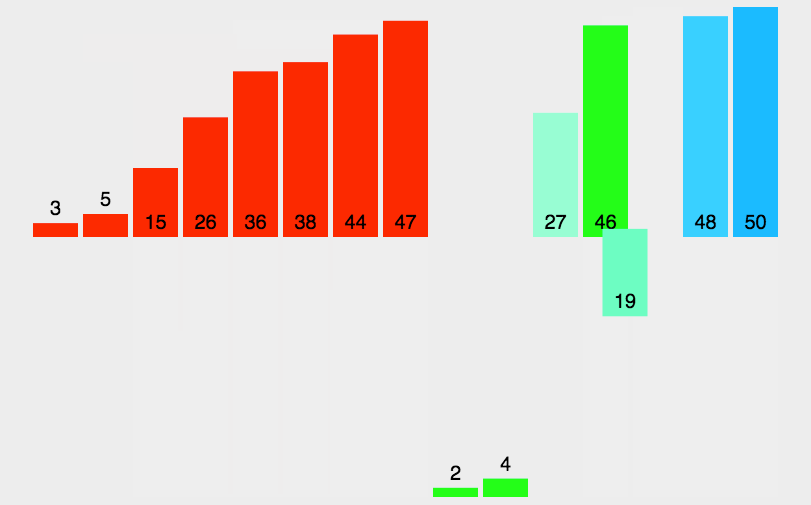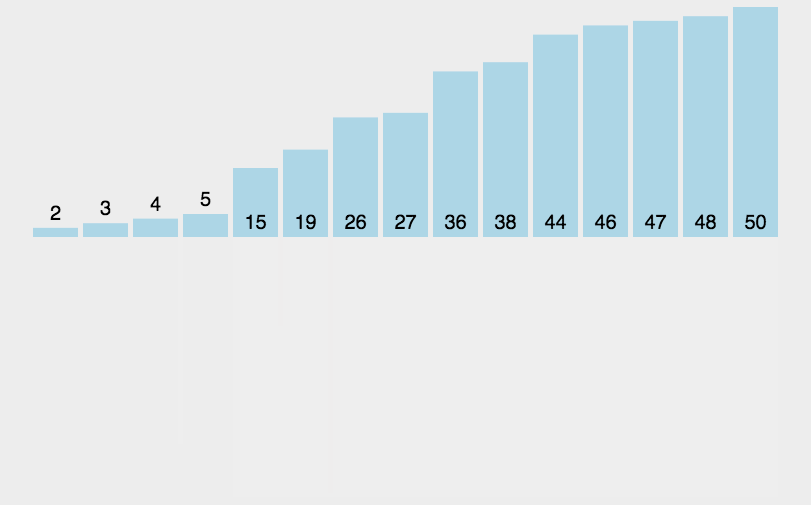
具体排序方法，以一组无序数列｛10，14，12，13，11，9｝为例分解说明，如下图所示：

由上图可知，二路归并排序首先把一个序列从中间分割成两部分，再把两部分的每部分又分割成两部分，依次分割下去，直到分割成的部分只有单一的数据，再把这些数据两两归并到一起，使之有序，继续归并下去，直到最后成为一个全部有序的序列。

从上面的描述可知，二路归并排序可以使用递归函数来实现：

//二路归并排序（升序排序）
//对r数组的r[s]～r[e-1]所有元素二路归并排序，tmp数组用来临时保存归并的结果
void MergeSort(int r[],int s,int e,int tmp[]){
	if(s+1==e) return;     //递归出口
	//递归拆分
	int mid = (s+e)/2;
	MergeSort(r,s,mid,tmp);   //r[s]～r[mid-1]
	MergeSort(r,mid,e,tmp);   //r[mid]～r[e-1]

	//有序的两个部分合并（这里的语句相当经典，大家注意体会） 
	int i = s,j = mid,k = s;
	while(i<mid && j<e){
		if(r[i]<=r[j]) tmp[k++] = r[i++];
		else tmp[k++] = r[j++];
	}

	//拷贝可能剩余的部分
	while(i<mid) tmp[k++] = r[i++];
	while(j<e) tmp[k++] = r[j++];

	//拷贝回原数组
	for(i=s;i<e;i++) r[i] = tmp[i];
}
//调用方法举例：MergeSort(a,0,10,b);
//调用方法举例：MergeSort(a,0,a+n,b);
//调用方法举例：MergeSort(a,1,a+n+1,b);

仿照 sort 函数的写法，用两个指针作为函数参数来指定排序的区域：

//二路归并排序：对指针begin~end区域排序（升序排序，不包括end）
//tmp数组用来临时保存归并的结果
void MergeSort(int *begin,int *end,int *tmp){
    if(begin+1==end) return;     //递归出口
    //递归拆分
    int *mid = begin+(end-begin)/2;   //两个指针不能相加，这里不能写成(begin+end)/2
    MergeSort(begin,mid,tmp);             //begin～mid-1
    MergeSort(mid,end,tmp+(mid-begin));   //mid～end-1，注意第三个参数 

    //有序的两个部分合并（这里的语句相当经典，大家注意体会） 
    int *p = begin,*q = mid,*k = tmp;
    while(p<mid && q<end){
        if(*p <= *q) *(k++) = *(p++);
        else *(k++) = *(q++);
    }

    //拷贝可能剩余的部分
    while(p<mid) *(k++) = *(p++);
    while(q<end) *(k++) = *(q++);

    //拷贝回原数组
    for(p=begin,k=tmp;p<end;p++,k++) *p = *k;
}
//调用方法举例：MergeSort(a,a+10,b);
//调用方法举例：MergeSort(a,a+n,b);
//调用方法举例：MergeSort(a+1,a+n+1,b);

二路归并排序的时间复杂度为 \(O(n\log{n})\)，算法还额外使用了一个和原始数组长度一致的数组来保存归并后的结果，所以算法的空间复杂度为 \(O(n)\)。从分割归并的过程来看，归并排序是稳定排序。

二、求逆序对

来看问题：P1908 逆序对

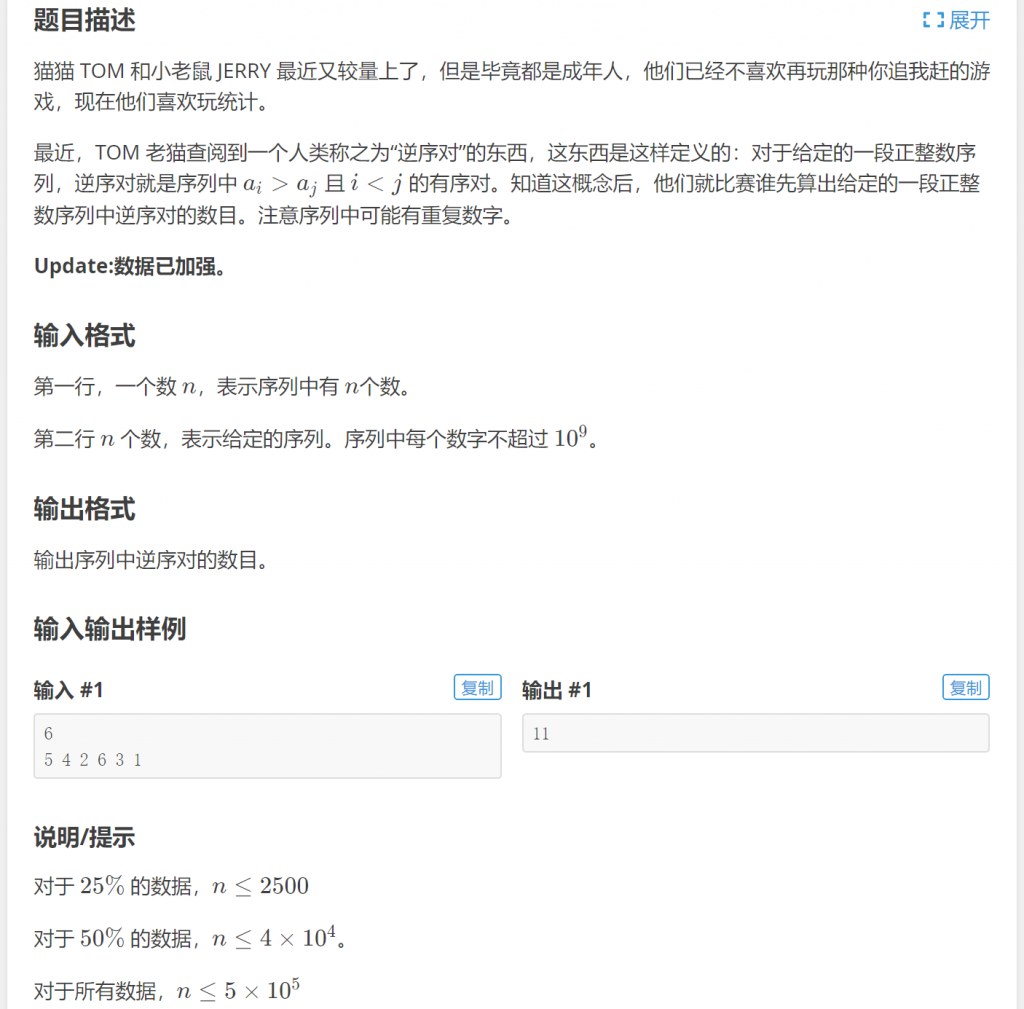
最简单的方法是用双重循环来模拟查找存储在数组中的逆序对：

#include<iostream>
using namespace std;
const int N = 500001;
int a[N];
int main()
{
	int n,cnt = 0;
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i];
	
	for(int i=1;i<n;i++){
		for(int j=i+1;j<=n;j++){
			if(a[i]>a[j]) cnt++;
		}
	}
	
	cout<<cnt<<endl;
	return 0;
} 

上面的程序只能过5个测试点，其他测试点均为超时TLE。因为算法的时间复杂度为 \(O(n^2)\)，数据规模一上来就很容易超时。需要重新设计算法。

我们来看归并排序合并的过程，需要注意的是合并前下图中数组的两个部分已经有序了：

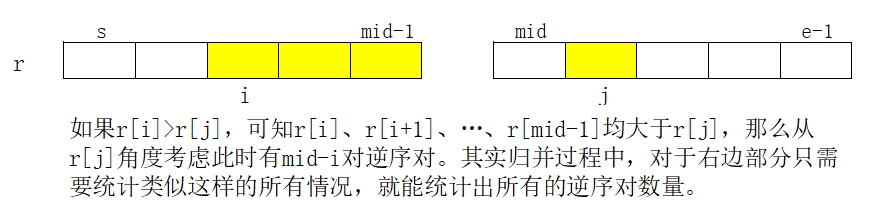
可知稍微修改一下归并排序函数就能计算出逆序对的数量：

#include<iostream>
using namespace std;
const int N = 500010;
int r[N],tmp[N];
long long cnt=0;         //全局变量统计逆序对数量

//原数组和用来合并的临时数组都用全局变量
void MergeSort(int s,int e){
    if(s+1==e) return;     //递归出口
    //递归拆分 
    int mid = (s+e)/2;
    MergeSort(s,mid);
    MergeSort(mid,e);

    //有序的两个部分合并 
    int i=s,j=mid,k=s;
    while(i<mid && j<e){
        if(r[i]<=r[j]) tmp[k++] = r[i++];
        else tmp[k++] = r[j++],cnt += mid-i;    //累加统计逆序对数量
    }

    //拷贝可能剩余的部分 
    while(i<mid) tmp[k++] = r[i++];
    while(j<e) tmp[k++] = r[j++];

    //拷贝回原数组 
    for(i=s;i<e;i++) r[i] = tmp[i];
}
int main()
{
    int n;
    cin>>n;
    for(int i=0;i<n;i++) cin>>r[i];
    MergeSort(0,n);
    cout<<cnt<<endl;
    return 0;
} 

上面算法的时间复杂度与归并排序一致，是 \(O(n\log{n})\)，能够通过全部测试点。