桶排序与基数排序

一、桶排序

桶排序（Bucket Sort）是计数排序的升级版。假设输入数据服从均匀分布，桶排序的工作原理：

1. 将数据分到有限数量的桶里：装入的时候确保桶 1，桶 2，桶 3……中装入的数据整体上是有序的，以按照升序排序为例，要保证桶 1 中装入的最大的数小于桶 2 中装入的最小的数，桶 2 中装入的最大的数小于桶 3 中装入的最小的数……
2. 每个桶再分别排序，有可能使用别的排序算法或是以递归方式继续使用桶排序进行排；
3. 最后再按序号依次将桶中的数汇总顺序排列，就是最终排序结果。

假设要排序的所有数据都是 1～99 的整数，那么可以以十位上的数字为标准将所有的数据放到编号为 0～9这 10 个“桶”中，然后对每个桶里的数据进行排序，最后将所有桶里的数据合并即是排序结果。

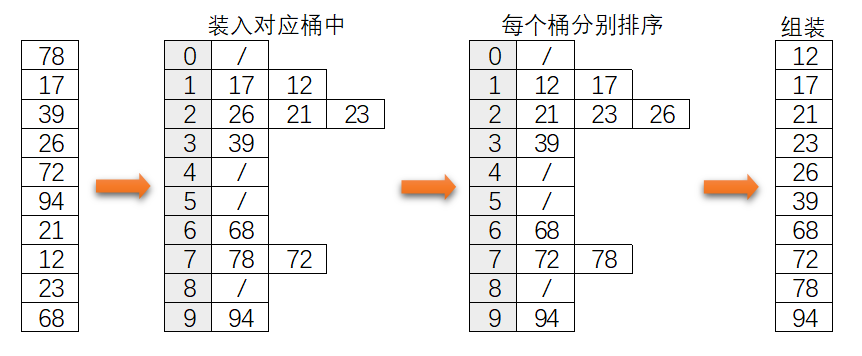
如果分成 99 个“桶”，那就成了计数排序，可见计数排序是桶排序的特例。

实际操作时，可以人为设定桶的数量，然后将每个要排序的数据映射存放到对应的桶里。

假定桶的数量为 $G$，排序数据的最大值是 $max$，最小值是 $min$。那么每个桶的大小（这里的大小指的是桶里能装数的最小值到最大值的跨度，并不是桶能装数的数量）是 $size = ceil((max-min)/G)$，对于序列中的某个数 $m$，它应该装在编号为 $(m-min)/size$ 的桶里。

const int N = 1000;
const int G = 5;      //桶数量
int r[N],tmp[G+1][N+1];
//桶排序：升序排序
//将全局数组r的r[s]～r[e-1]区间排序，要使用一个全局二维数组tmp 
void BucketSort(int s,int e){    
    //计算最大值、最小值 
    int max = r[s],min = r[s];
    for(int i=s+1;i<e;i++){
        if(r[i]>max) max = r[i];
        if(r[i]<min) min = r[i];
    }
    
    //计算每个桶的大小（桶里能装数的最小值到最大值的跨度，并不是桶能装数的数量） 
    int size = (max-min)/G;
    if((max-min)%G) size++;
    
    //每个桶里数据数量清零
    for(int i=0;i<G;i++) tmp[i][0] = 0; 
    //每个数分到对应桶里
    for(int i=s;i<e;i++){
        int g = (r[i]-min)/size;
        tmp[g][++tmp[g][0]] = r[i];
    }
    
    //桶内数据排序并拷贝回原数组中 
    for(int i=0;i<=G;i++){   //注意：这里是i<=G 
        if(!tmp[i][0]) continue;
        //对第i个桶里的数据排序，这里直接用sort函数来处理了（可以换成快排等排序算法） 
        sort(tmp[i]+1,tmp[i]+tmp[i][0]+1);
        for(int k=1;k<=tmp[i][0];k++) r[s++] = tmp[i][k];
    }
}
//调用方法举例：BucketSort(0,10);
//调用方法举例：BucketSort(0,n);

桶排序最好情况下使用线性时间 $O(n)$，桶排序的时间复杂度，取决与对各个桶之间数据进行排序的时间复杂度，因为其它部分的时间复杂度都为 $O(n)$。桶排序使用了额外的数组，空间复杂度是 $O(n)$。很显然，桶划分的越小，各个桶之间的数据越少，排序所用的时间也会越少，但相应的空间消耗就会增大。

二、基数排序

基数排序（Radix Sort）算法很特殊，它不需要直接对元素进行相互比较，也不需要将元素相互交换，需要做的就是对元素进行“分类”。这也是基数排序的魅力所在，基数排序可以理解成是建立在“计数排序”的基础之上的一种排序算法。在实际项目中，如果对效率有所要求，而不太关心空间的使用时，基数排序是一种不错的选择。我们先通过动图了解一下基数排序的过程：

以序列 {556 ,3 ,49 ,26 ,81 ,9 ,863 ,0 ,27 ,25} 为例，下图展示了基数排序的细节：

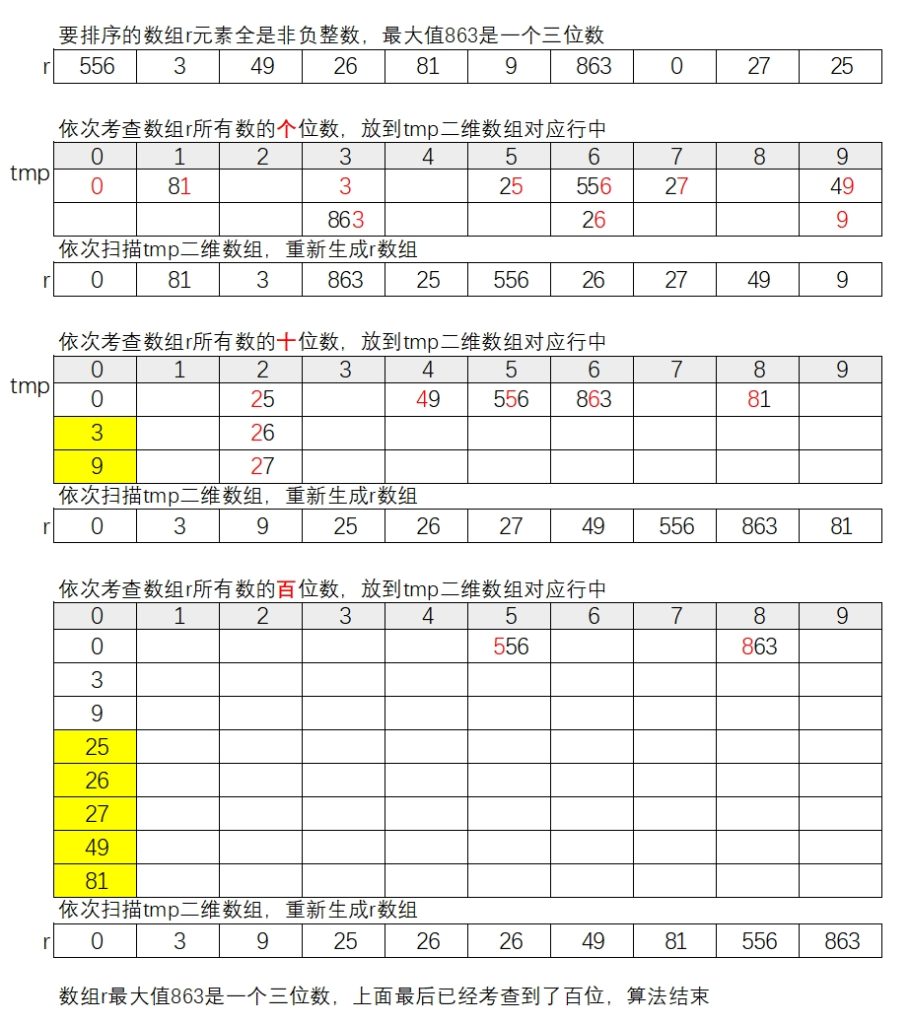
需要特别注意的是，基数排序适用于元素都是非负整数的序列。下面给出基数排序的参考代码：

const int N = 1000;
int r[N],tmp[10][N+1];
//基数排序：升序排序
//将全局数组r（所有元素是非负整数）的r[s]～r[e-1]区间排序，要使用一个全局二维数组tmp 
void RadixSort(int s,int e){    
    //计算最大值 
    int max = r[s];
    for(int i=s+1;i<e;i++){
        if(r[i]>max) max = r[i];
    }
    
    //计算最大值的位数
    int size = 0;
    while(max) size++,max/=10;
    if(size==0) size++;
    
    //基数排序过程（按照个位、十位、百位、…上的数字依次分类） 
    for(int i=1,power=1;i<=size;i++,power*=10){
        //tmp数组每一行第一个元素记录数量，每次处理前先清零 
        for(int j=0;j<=9;j++) tmp[j][0] = 0;
        
        //将r数组中的每个数据按照从个位到高位第i位的数字k存放到tmp[k]中 
        for(int j=s;j<e;j++){
            int k = r[j]/power%10;         //k是r[j]从个位到高位第i位的数字 
            tmp[k][++tmp[k][0]] = r[j];    //将r[j]存储到数组tmp[k]的末尾 
        }
        
        //将tmp数组中的数据依次拷贝到r数组中 
        for(int j=0,tot=s;j<=9;j++){
            for(int k=1;k<=tmp[j][0];k++) r[tot++] = tmp[j][k]; 
        }    
    }
}
//调用方法举例：RadixSort(0,10);
//调用方法举例：RadixSort(0,n);

基数排序分别归类收集，所以是稳定的，时间复杂度可以粗略认为是 $O(n)$，但是上面的基数排序只能处理元素是非负整数的数组。