循环枚举——P3392 涂国旗

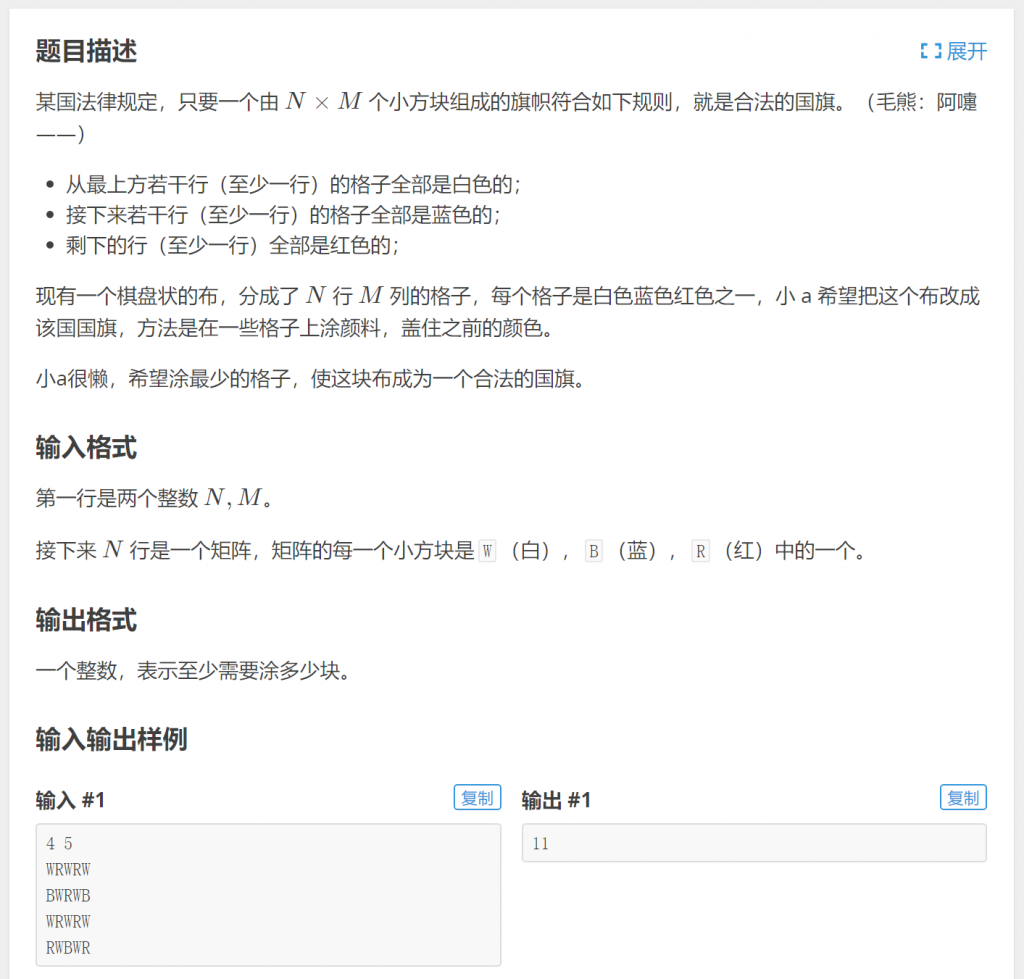
来看例题：P3392 涂国旗

国旗从上到下分成三个颜色区域，可以使用双重循环枚举白色区域的高度$w$和蓝色区域的高度$b$，那么剩下的就是红色区域，高度为$n-w-b$。可知$1 \le w \le n-2$，$1 \le b \le n-w-1$：

for(int w=1;w<=n-2;w++){			//白色区域高度 
	for(int b=1;b<=n-w-1;b++){	  //蓝色区域高度 
		//1～w行是白色区域
		//w+1～w+b行是蓝色区域
		//w+b+1～n行是红色区域 
	}
}

双重循环的最内层就对应了一个方案。接下来需要计算：1～$w$行全部格子涂成白色需要涂改的格子数量、$w+1$～$w+b$行全部格子涂成蓝色需要涂改的格子数量、$w+b+1$～$n$行全部格子涂成红色需要涂改的格子数量，上述三种涂改格子数量的和就是本方案全部涂改格子的数量，通过打擂比较得出所有方案最小涂改格子数量即可。显然，又需要在双重循环的内部通过三个双重循环循环来计算三个区域需要涂改的格子数量：

#include<iostream>
using namespace std;
char a[55][55];
int main()
{
	int n,m,ans,cnt;
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			cin>>a[i][j];
		}
	}
	ans = n*m;
	for(int w=1;w<=n-2;w++){			//白色区域高度 
		for(int b=1;b<=n-w-1;b++){	  //蓝色区域高度
			cnt = 0; 
			//1～w行是白色区域
			for(int i=1;i<=w;i++){
				for(int j=1;j<=m;j++) cnt += a[i][j]!='W';
			}
			//w+1～w+b行是蓝色区域
			for(int i=w+1;i<=w+b;i++){
				for(int j=1;j<=m;j++) cnt += a[i][j]!='B';
			}
			//w+b+1～n行是红色区域
			for(int i=w+b+1;i<=n;i++){
				for(int j=1;j<=m;j++) cnt += a[i][j]!='R';
			}
			if(cnt<ans) ans = cnt;
		}
	}
	cout<<ans<<endl;
    return 0;
}

算法的时间复杂度是$O(mn^3)$，因为问题数据规模并不大（对于$100\%$的数据$N,M \le 50$），所以上面的比较原始的暴力循环枚举依然能够顺利通过所有测试点。

现在来思考如何优化枚举方案，提高程序效率。对于这个问题，双重循环来枚举白色、蓝色区域的高度是不可避免的，但是仔细思考双重循环内部，每次都计算了将一个区域所有格子修改成某种颜色需要涂改格子的数量。在程序运行时，每种方案都进行这样的计算，这样就出现了大量重复不必要的计算。那么能否将这些计算预先完成呢？例如在进入枚举的循环前先计算好每一行涂改成三种颜色需要涂改的格子数量，那么在循环内就可以减少大量不需要的重复计算：

#include<iostream>
using namespace std;
int W[55],B[55],R[55];
int main()
{
	char c;
	int n,m;
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		//计算第i行涂改成三种颜色需要涂改的格子数量 
		W[i] = B[i] = R[i] = m;	//需要涂改的格子数量初始值都为m 
		for(int j=1;j<=m;j++){
			cin>>c;
			//颜色为W，那么将第i行全部涂改成W，需要涂改的格子数量-1
			if(c=='W') W[i]--;
			else if(c=='B') B[i]--;
			else if(c=='R') R[i]--;
		}
	}
	//...
    return 0;
}

上面程序片段的功能是将第$i$行所有格子涂改成白色、蓝色、红色需要涂改的格子数量分别记录到$W[i]$、$B[i]$、$R[i]$中，算法的时间复杂度降低到$O(n^3)$。那么接下来的处理就能避免大量重复的计算：

#include<iostream>
using namespace std;
int W[55],B[55],R[55];
int main()
{
	char c;
	int n,m,ans,cnt;
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		//计算第i行涂改成三种颜色需要涂改的格子数量 
		W[i] = B[i] = R[i] = m;	//需要涂改的格子数量初始值都为m 
		for(int j=1;j<=m;j++){
			cin>>c;
			//颜色为W，那么将第i行全部涂改成W，需要涂改的格子数量-1
			if(c=='W') W[i]--;
			else if(c=='B') B[i]--;
			else if(c=='R') R[i]--;
		}
	}
	ans = n*m;
	for(int w=1;w<=n-2;w++){			//白色区域高度 
		for(int b=1;b<=n-w-1;b++){	  //蓝色区域高度
			cnt = 0; 
			//1～w行是白色区域
			for(int i=1;i<=w;i++) cnt += W[i];
			//w+1～w+b行是蓝色区域
			for(int i=w+1;i<=w+b;i++) cnt += B[i];
        	//w+b+1～n行是红色区域
			for(int i=w+b+1;i<=n;i++) cnt += R[i]; 
			if(cnt<ans) ans = cnt;
		}
	}
	cout<<ans<<endl;
    return 0;
}

其实还可以再优化，可以在循环枚举前计算将第1行到第$i$行所有格子涂改成白色、蓝色、红色需要涂改的格子数量，分别记录到$W[i]$、$B[i]$、$R[i]$中，那么在双重循环内部就可以避免再使用循环计算修改颜色的格子数量了，算法的时间复杂度降低到$O(n^2)$。

1. $1～w$ 行涂改成白色，需要涂改颜色的格子数量是：$W[w]$;
2. $w+1～w+b$ 行涂改成蓝色，需要涂改颜色的格子数量是：$B[w+b]-B[w]$;
3. $w+b+1～n$ 行涂改成红色，需要涂改颜色的格子数量是：$R[n]-R[w+b]$;

这样做其实是运用了“前缀和”的思想：

#include<iostream>
using namespace std;
int W[55],B[55],R[55];
int main()
{
	char c;
	int n,m,ans,cnt;
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		//计算第i行涂改成三种颜色需要涂改的格子数量 
		W[i] = B[i] = R[i] = m;	//需要涂改的格子数量初始值都为m 
		for(int j=1;j<=m;j++){
			cin>>c;
			//颜色为W，那么将第i行全部涂改成W，需要涂改的格子数量-1
			if(c=='W') W[i]--;
			else if(c=='B') B[i]--;
			else if(c=='R') R[i]--;
		}
		//修改成从第1行到第i行涂改成三种颜色需要涂改的格子数量 
		W[i] += W[i-1];
		B[i] += B[i-1];
		R[i] += R[i-1];
	}
	ans = n*m;
	for(int w=1;w<=n-2;w++){			//白色区域高度 
		for(int b=1;b<=n-w-1;b++){	  //蓝色区域高度
			cnt = 0; 
			//1～w行是白色区域
			cnt += W[w];
			//w+1～w+b行是蓝色区域
			cnt += B[w+b]-B[w];
        	//w+b+1～n行是红色区域
			cnt += R[n]-R[w+b]; 
			if(cnt<ans) ans = cnt;
		}
	}
	cout<<ans<<endl;
    return 0;
}