来看例题:P2241 统计方形(数据加强版)
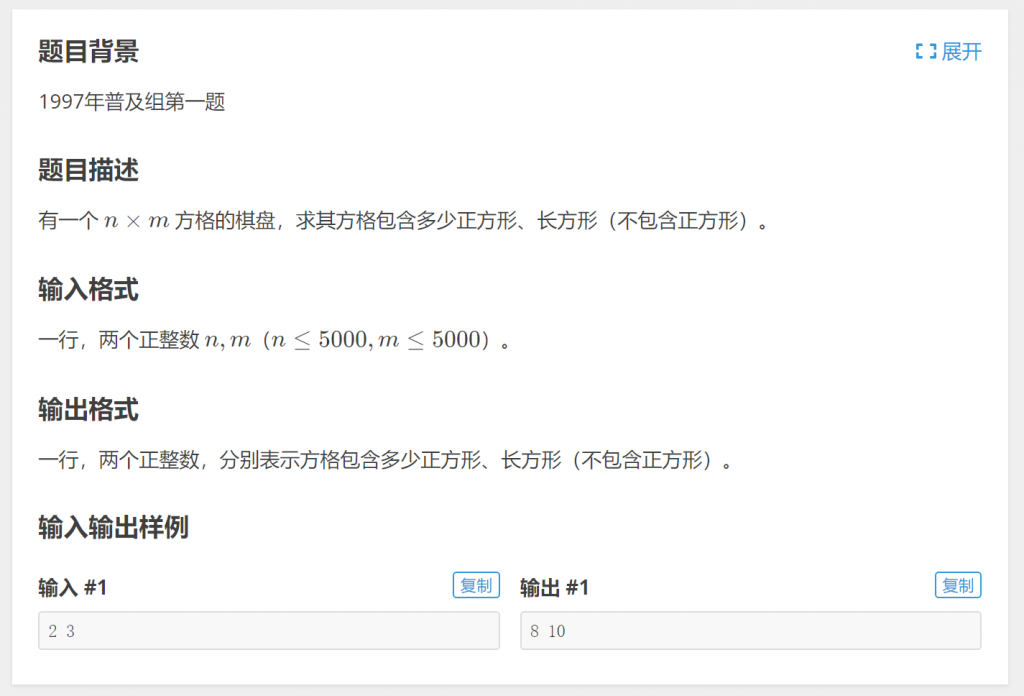
首先来考虑棋盘中正方形和长方形的特征,可以得出一个明显的结论:棋盘中不同行不同列的两个点能够确定一个正方形或者长方形。
但是究竟是正方形还是长方形需要进一步考查两点的坐标关系(通过坐标计算两条边长来确定)。那可以枚举两个点的坐标情况,第一个点有\((n+1) \times (m+1)\)种可能,第二个点也有\((n+1) \times (m+1)\)种可能,可知算法时间复杂度是\(O(n^2m^2)\)。看数据规模(\(n,m \le 5000\)),很明显会超时。并且这样的统计结果中会出现大量重复统计的正方形和长方形,还需要想办法排除。通过上述分析可知,枚举不同行不同列的两个点这样的策略是不可取的。
优化思路一:如果只枚举一个点,统计以该点为顶点的正方形和长方形的数量,那么只需要枚举\((n+1) \times (m+1)\)个坐标点即可,算法时间复杂度降低到\(O(nm)\)。实际上这样做确实也能统计出结果:
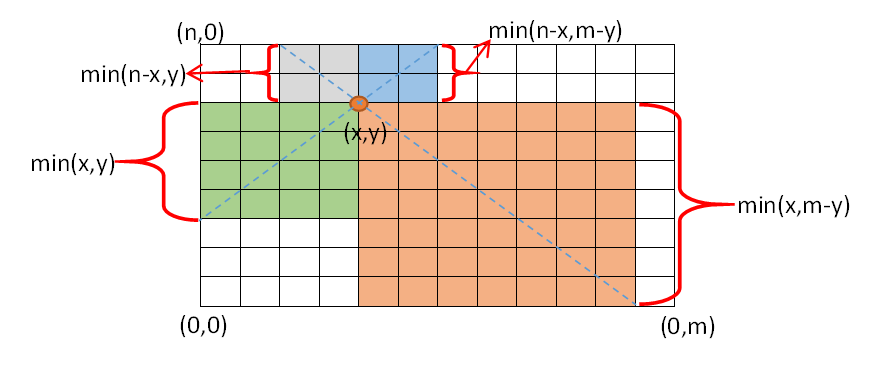
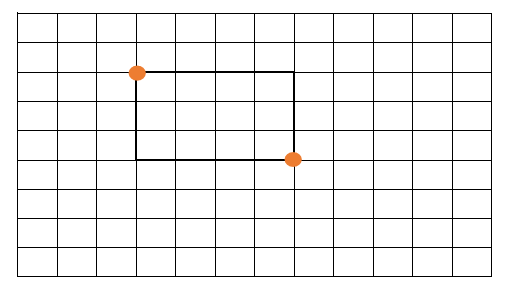
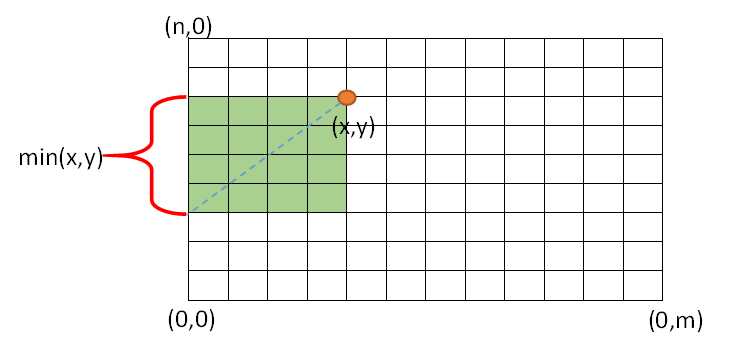
如上图所示,设棋盘左下角为坐标原点\(O(0,0)\),行方向竖直向上,列方向水平向右,那么\(x\)行\(y\)列这一点的坐标是\((x,y)\)。先来考虑以这一点为顶点的正方形的数量,不计算点\((x,y)\),图中虚线上的每一个点都能和\((x,y)\)构成一个正方形,通过对图中四个不同区域的统计可知坐标点\((x,y)\)确定的正方形数量是\(min(x,y)+min(n-x,y)+min(x,m-y)+min(n-x,m-y)\)。
那么长方形呢?其实棋盘中与\((x,y)\)不同行不同列的点都能和\((x,y)\)组成矩形,这些点的数量(也就是矩形的数量)正好是\(n \times m\),排除掉正方形就是长方形。
还有一个问题,上面的统计方案出现了重复统计的情况:
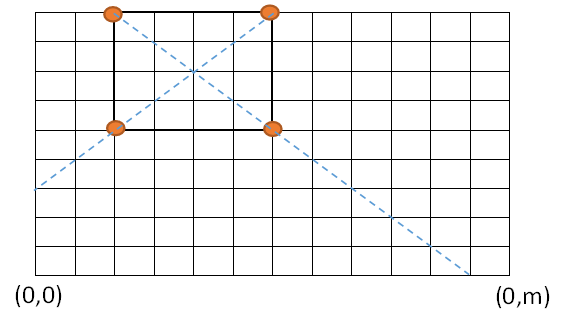
如上图所示,对于标识出来的粗边正方形会被它的四个顶点各统计一次,一共统计了4次。其实可以证明上面的统计策略,所有的正方形和长方形都被统计了4次,那么最终结果还需要除以4。实际编程时,我们通过多组测试样例也能发现这个问题并及时修正(有测试样例就是香O(∩_∩)O~)。
#include<bits/stdc++.h>
using namespace std;
int main()
{
int n,m;
long long squ = 0,rect = 0;
cin>>n>>m;
for(int x=0;x<=n;x++){
for(int y=0;y<=m;y++){
int one = min(x,y)+min(n-x,y)+min(x,m-y)+min(n-x,m-y);
squ += one;
rect += n*m-one;
}
}
cout<<squ/4<<" "<<rect/4<<endl;
return 0;
}
优化思路二:上面的策略出现了重复统计的情况,能否进一步优化呢?其实对于\(x\)行\(y\)列这一点\((x,y)\)可以只考虑以该点为右上角顶点的正方形和长方形数量,那么就能避免重复统计的情况。可知正方形的数量是\(one = min(x,y)\),矩形的数量是\(x \times y\),长方形的数量是\(x \times y \ - one\)。
#include<bits/stdc++.h>
using namespace std;
int main()
{
int n,m;
long long squ = 0,rect = 0;
cin>>n>>m;
for(int x=1;x<=n;x++){
for(int y=1;y<=m;y++){
int one = min(x,y);
squ += one;
rect += x*y-one;
}
}
cout<<squ<<" "<<rect<<endl;
return 0;
}
优化思路三:可以尝试枚举棋盘内矩形的边长。可知棋盘内小矩形的竖直纵向边的边长\(a\)可以是1~\(n\)中的任意一个整数,另外一边(水平横向边)的边长\(b\)可以是1~\(m\)中的任意一个整数。
通过画图可知,边长为\(a\)的竖直纵向边一共有\(n-a+1\)种放置方法,边长为\(b\)的水平横向边一共有\(m-b+1\)种放置方法,那么一共有\((n-a+1) \times (m-b+1)\)个“竖直纵向边边长为\(a\)、水平横向边边长\(b\)”的矩形,其中\(a==b\)时是正方形,其余均是长方形。
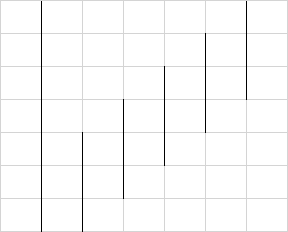
一共有5种放置方法(\(n-a+1\))
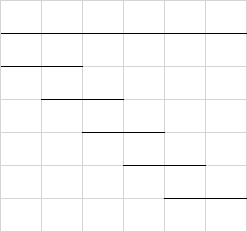
一共有5种放置方法(\(m-b+1\))
#include<bits/stdc++.h>
using namespace std;
int main()
{
int n,m;
long long squ = 0,rect = 0;
cin>>n>>m;
for(int a=1;a<=n;a++){
for(int b=1;b<=m;b++){
if(a==b) squ += (n-a+1)*(m-b+1);
else rect += (n-a+1)*(m-b+1);
}
}
cout<<squ<<" "<<rect<<endl;
return 0;
}
优化思路四:其实矩形的数量是可以直接用公式计算出来的,可以枚举矩形的四条边,这里以枚举水平横向的两条边为例:
- 第一条边放在直线\(x=0\)上时,第二条边可以放在直线\(x=1\)、\(x=2\)、…、\(x=n\)上,有\(n\)种放置方法;
- 第一条边放在直线\(x=1\)上时,为了不和前面的情况重复,第二条边可以放在直线\(x=2\)、\(x=3\)、…、\(x=n\)上,有\(n-1\)种放置方法;
- 第一条边放在直线\(x=2\)上时,为了不和前面的情况重复,第二条边可以放在直线\(x=3\)、\(x=4\)、…、\(x=n\)上,有\(n-2\)种放置方法;
- ……
- 第一条边放在直线\(x=n-1\)上时,为了不和前面的情况重复,第二条边只能放在直线\(x=n\)上,有\(1\)种放置方法;
可知两条水平横向边的放置方案有\(1+2+3+...+n\),也就是\(\frac{1}{2}n(n+1)\)种(高中数学等差数列求和公式),同理两条竖直纵向边的放置方案有\(\frac{1}{2}m(m+1)\)种。那么矩形的数量总数是\(\frac{1}{4}nm(n+1)(m+1)\),接下来只需要计算正方形的数量即可。
计算正方形的数量,可以按照上一个方案来枚举正方形的边长,可知正方形的边长\(a\)可以是1~\(min(n,m)\)中的任意整数。边长为\(a\)的竖直纵向边一共有\(n-a+1\)种放置方法,边长为\(a\)的水平横向边一共有\(m-a+1\)种放置方法,那么一共有\((n-a+1) \times (m-a+1)\)个边长为\(a\)的正方形。
#include<bits/stdc++.h>
using namespace std;
int main()
{
long long n,m; //注意细节,这里n,m都是long long
long long squ = 0,rect;
cin>>n>>m;
for(int a=1;a<=min(n,m);a++){
squ += (n-a+1)*(m-a+1);
}
rect = n*m*(n+1)*(m+1)/4-squ; //如果n,m是int,这里乘法可能出现数据溢出
cout<<squ<<" "<<rect<<endl;
return 0;
}
循环枚举算法时间复杂度降低到\(O(n)\)。这里还可以进一步优化:
观察循环中的语句,这里设 \(t = min(n,m)\),可知:
\(squ = nm+(n-1)(m-1)+(n-2)(m-2)+...+(n-t+1)(m-t+1)\)。做乘法运算,会得到:
\(squ=nm+[nm-(n+m)+1]+[nm-2(n+m)+4]+...+[nm-(t-1)(n+m)+(t-1)^2]\)整理得到:\(squ=tnm-[1+2+...+(t-1)](n+m)+[1^2+2^2+...+(t-1)^2]\)
结合等差数列求和公式和连续平方和公式,最后可以化简为:\(squ=tnm-\frac{t(t-1)(n+m)}{2}+\frac{t(t-1)(2t-1)}{6}\)
#include<bits/stdc++.h>
using namespace std;
int main()
{
long long n,m,t; //注意细节,这里n,m,t都是long long
long long squ = 0,rect;
cin>>n>>m;
t = min(n,m);
squ = t*m*n-t*(t-1)*(m+n)/2+t*(t-1)*(2*t-1)/6;
rect = n*m*(n+1)*(m+1)/4-squ;
cout<<squ<<" "<<rect<<endl;
return 0;
}
通过优化,最终将循环枚举算法时间复杂度降低到\(O(1)\)。
针对这个问题,通过改变不同的枚举要素(枚举矩形的两个点 \(→\) 枚举矩形的一个点 \(→\) 枚举作为矩形右上角顶点的那个点)来减少枚举量,降低算法的时间复杂度并让程序代码更加简洁。最后从枚举矩形的边长出发,通过枚举计算正方形数量,并通过数学推理得出计算矩形数量的公式,进一步减少了循环枚举的层级,提高了程序的执行效率。
 NOIP学习小站
NOIP学习小站