子集枚举

先来看一个问题，从 1～$n$ 中选择 4 个数，有多少种选择方法？输出具体的选择方案。

这是一个数学的组合问题，组合不讲顺序（选出来的数不考虑它们位置关系），例如 {1,2,3,4} 和 {1,2,4,3}、{1,3,2,4}、{1,3,4,2}……都是同一种选法。从采用循环枚举的策略，第一个数 i1 枚举 1～(n-3) 的所有数，为了避免重复，第二个数 i2 枚举 (i1+1)～(n-2) 的所有数，第三个数 i3 枚举 (i2+1)～(n-1) 的所有数，第四个数 i4 枚举 (i3+1)～n 的所有数：

#include<iostream>
using namespace std;
int main(){
	int n,cnt = 0;
	cin>>n;
	for(int i1=1;i1<=n-3;i1++){
		for(int i2=i1+1;i2<=n-2;i2++){
			for(int i3=i2+1;i3<=n-1;i3++){
				for(int i4=i3+1;i4<=n;i4++){
					cout<<i1<<" "<<i2<<" "<<i3<<" "<<i4<<endl;
					cnt++;
				}
			}
		}
	}
	cout<<cnt<<endl;
    return 0;
}

数学知识—排列：从 $n$ 个不同数中选择 $m$ 个数进行排列（排列考虑选出来的 $m$ 个数的先后顺序，例如 {1,2,3,4} 和 {1,2,4,3}、{1,3,2,4}、{1,3,4,2}……是不同的排列），这样选出来并按不同顺序排列的方案数量称为排列数，数学中记排列数量为 $\mathrm{A}_n^m$。可知第 $1$ 个数有 $n$ 种选法，第 $2$ 个数有 $n-1$ 种选法，第 $3$ 个数有 $n-2$ 种选法，……，第 $m$ 个数有 $n-m+1$ 种选法：
根据乘法原理，一共有 $n \times (n-1) \times (n-2) \times ... \times (n-m+1)$ 种排列方法，
也就是 $\mathrm{A}_n^m = n \times (n-1) \times (n-2) \times ... \times (n-m+1)=\frac{n!}{(n-m)!}$。
如果从 $n$ 个不同数中选择 $n$ 个数进行排列（所有数进行排列），这就是全排列，可知 $\mathrm{A}_n^n = n!$。

数学知识—组合：从 $n$ 个不同数中选择 $m$ 个数的方案数量称为组合数，组合不讲顺序，数学中记组合数为 $\mathrm{C}_n^m$。其实排列方案中就包含了组合方案：由于排列考虑顺序，对于选择 $m$ 个数的每个组合方案，这 $m$ 个数的全排列数是$\mathrm{A}_m^m$，所以这个组合在排列方案中会出现 $\mathrm{A}_m^m$ 次，由此可知 $\displaystyle \mathrm{C}_n^m=\frac{\mathrm{A}_n^m}{\mathrm{A}_m^m}=\frac{\mathrm{A}_n^m}{m!}=\frac{n!}{(n-m)! \times m!}$。

杨辉三角形第 $n$ （从 $0$ 行算起）行第 $m$ （从 $0$ 开始）个数就是 $C_n^m$ 的结果（$C_n^0=1，C_n^n=1$），由杨辉三角每行的对称性可以得出组合的一个特殊性质：$C_n^m = C_n^{n-m}$（从 $n$ 个数中选择 $m$ 个数的每种方案都对应了一种从 $n$ 个数中选择 $n-m$ 个数的方案）。由杨辉三角中任意一个数是前一行“肩上”两数的和还可以得出组合的另一个特殊性质：$C_n^m = C_{n-1}^{m-1}+C_{n-1}^m$。

如果是选择更多的数，用上面的多重循环实现过于复杂。进一步，如果选择的数的数量是一个变量，是无法用多重循环处理的。此时可以用下面的子集枚举策略来实现，后面我们还可以使用搜索算法来实现子集枚举。

除了本文介绍的子集枚举算法外，后面还会介绍使用搜索算法实现子集枚举。

集合是高中数学内容，集合可以认为是若干数据的组合，集合 $U$ 的子集可以认为是集合 $U$ 的一部分元素组成的集合。假设集合 $U=\{1,2,3,4,5\}$，可知集合 $U_1=\{1,2\}$、$U_2=\{1,3,4,5\}$、$U_3=\{1,4\}$、$U_4=\{3\}$ 都是 $U$ 的子集。子集可以用全集 $U$ 中的元素有没有出现来描述，用 1 表示元素出现，0 表示元素没有出现，那么上面的子集可以描述如下：

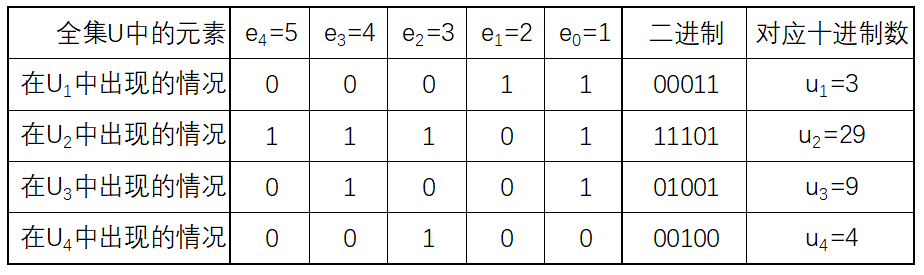
表里的做法就是二进制的每一位标识了一个元素是否出现：1表示出现，0表示未出现。例如二进制的最低位就标识了第0个元素1是否出现，次低位标识了第1个元素2是否出现……

从上面的分析可知，用 1、0 来表示全集 $U$ 中的元素是否出现，那么每个子集可以描述成互不相同的二进制数，并且还可以进一步描述为互不相同的十进制数（取值范围 $0～ 2^n-1$ ）。反过来 $0～ 2^n-1$ 范围内的每个整数也对应了一个子集。 $n$ 个元素的集合的所有子集（包括空集和自身）数量为 $2^n$ 个。

如果集合 $U$ 中有 $n$ 个元素，分别是 $\{e_{n-1},...,e_2,e_1,e_0\}$，那么：

1. 包含所有元素的全集 $U$ 可以表示为(1<<n)-1；
2. 仅包含第 $i$（$0 \le i \le n-1$）个元素的集合 $\{e_i\}$ 对应的十进制可以用位运算描述为 1<<i（二进制数第 i 位是1，其他位都是0）；
3. 不包含任何元素的空集可以表示为 0。

这里的<<是左移运算，用来将整数按二进制整体左移，左移后右边补 0。n<<1 相等于 $n \times 2$，n<<m 相当于 $n \times 2^m$。

假设集合 $U$ 的子集 $U_i$ 用上面描述方法对应的十进制数是 $u_i$，集合 $U_1$ 对应的十进制描述结果为 $u1$，集合 $U_2$ 对应的十进制描述结果为 $u2$。我们来看集合的一些特殊操作：

1. 交集。两个集合的交集就是这两个集合公共元素组成的集合。子集 $U_1$、$U_2$ 的交集就是 u1&u2。这里的 & 是按位与运算，参加运算的两个整数，按二进制位进行“与”运算。
2. 并集。两个集合的并集就是包含这两个集合所有元素的集合（去重）。子集 $U_1$ 、$U_2$ 的并集就是 u1|u2。这里的 | 是按位或运算，参加运算的两个整数，按二进制位进行“或”运算。
3. 补集。补集指的是全集去掉某个集合所有元素后剩下元素组成的集合。子集 $U_1$ 对于全集 $U$ 的补集是((1<<n)-1)^u1。这里的 ^ 是按位异或运算，参加运算的两个整数，按二进制位进行“异或”运算。
4. 判断包含关系。集合 $U_1$ 的所有元素在 $U_2$ 中都出现，那么称 $U_2$ 包含 $U_1$，此时 $U_1$ 与 $U_2$ 的并集是 $U_2$，$U_1$ 与 $U_2$ 的交集是 $U_1$。那么 $U_2$ 包含 $U_1$ 的判断条件可以写成：(u2==u1|u2) && (u1==u1&u2)。
5. 判断属于关系。判断第 $i$ 个元素 $e_i$ 是否在子集 $U_1$ 中，可以转变为判断仅包含元素 $e_i$ 的子集 $\{e_i\}$ 与 $U_1$ 的交集不为空集。前面介绍了仅包含第 $i$（$0 \le i \le n-1$）个元素的集合 $\{e_i\}$ 对应的十进制可以用位运算描述为 1<<i，那么第 $i$ 个元素 $e_i$ 属于子集 $U_1$ 的判断条件为 (1<<i)&u1!=0。也可以判断 $u1$ 对应的二进制数的第 $i$ 位是否为 1，判断条件仍然是 (1<<i)&u1!=0。

来看例题：P1036 选数

首先，来看通过上面的方法来枚举所有的子集：

#include<iostream>
using namespace std;
int e[20];
int main()
{
    int n;
    cin>>n;
    for(int i=0;i<n;i++) cin>>e[i]; 
    int U = (1<<n)-1;
    //枚举每一个子集（对应的十进制数）
    for(int S=0;S<=U;S++){ 
        //判断第i个数是否在子集S中
        for(int i=0;i<n;i++){
			//整数S对应的二进制数第i位为1 
            if(S&(1<<i)) cout<<e[i]<<" ";
        }
        cout<<endl;
    }
    return 0;
}

找 n 选 k 的组合，可以转化为找元素数量是 k 的子集：

#include<iostream>
using namespace std;
int e[20],one[20];
int main()
{
    int n,k,ans = 0;
    cin>>n>>k;
    for(int i=0;i<n;i++) cin>>e[i]; 
    int U = (1<<n)-1;            //全集（对应的十进制数） 
    for(int S=0;S<=U;S++){       //枚举每一个子集（对应的十进制数） 
        int cnt = 0;
        for(int i=0;i<n;i++){    //判断第i个数在子集S中 
            if(S&(1<<i)) one[cnt++] = e[i];
        }
        //子集一共k个元素 
        if(cnt==k) {
        	ans++;
        	for(int i=0;i<k;i++) cout<<one[i]<<" ";
        	cout<<endl;
		}
    }
    cout<<ans;
    return 0;
}

要解决上面的问题，可以枚举所有的子集，对于每一个子集判断子集内元素的数量如果等于 k 并且所有元素的和是素数，那么就找到一种组合：

#include<iostream>
using namespace std;
int e[20];
//判断素数 
bool isPrime(int n){
	if(n<=1) return false;
	for(int i=2;i*i<=n;i++){
		if(n%i==0) return false;
	}
	return true;
}
int main()
{
	int n,k,ans = 0;
	cin>>n>>k;
	for(int i=0;i<n;i++) cin>>e[i]; 
	int U = (1<<n)-1;			//全集（对应的十进制数） 
	for(int S=0;S<=U;S++){	   //枚举每一个子集（对应的十进制数） 
		int cnt = 0,sum = 0;
		for(int i=0;i<n;i++){	//判断第i个数在子集S中 
			if(S&(1<<i)) cnt++,sum += e[i];
		}
		//子集一共k个元素并且和是素数 
		if(cnt==k && isPrime(sum)) ans++;
	}
	cout<<ans;
    return 0;
}

额外补充：可以使用内置函数 __builtin_popcount(n) 来计算整数 n 对应二进制数中 1 的个数，这个函数的效率极高，通常是CPU单指令实现，不过要关注编译器是否支持调用内置函数；还可以使用Brian Kernighan算法来快速计算整数 n 对应二进制数中 1 的个数。

#include<iostream>
using namespace std;
int e[20];
//判断素数 
bool isPrime(int n){
    if(n<=1) return false;
    for(int i=2;i*i<=n;i++){
        if(n%i==0) return false;
    }
    return true;
}
int main()
{
    int n,k,ans = 0;
    cin>>n>>k;
    for(int i=0;i<n;i++) cin>>e[i]; 
    int U = (1<<n)-1;            //全集（对应的十进制数） 
    for(int S=0;S<=U;S++){       //枚举每一个子集（对应的十进制数）
        if(__builtin_popcount(S)!=k) continue; 
        int sum = 0;
        for(int i=0;i<n;i++){    //判断第i个数在子集S中 
            if(S&(1<<i)) sum += e[i];
        }
        //子集一共k个元素并且和是素数 
        if(isPrime(sum)) ans++;
    }
    cout<<ans;
    return 0;
}

// Brian Kernighan算法（O(m)时间复杂度，m为1的个数）
int countBits(int num) {
    int count = 0;
    while (num) {
        num &= (num - 1); // 清除最低位的1
        count++;
    }
    return count;
}

再来看问题：P1157 组合的输出

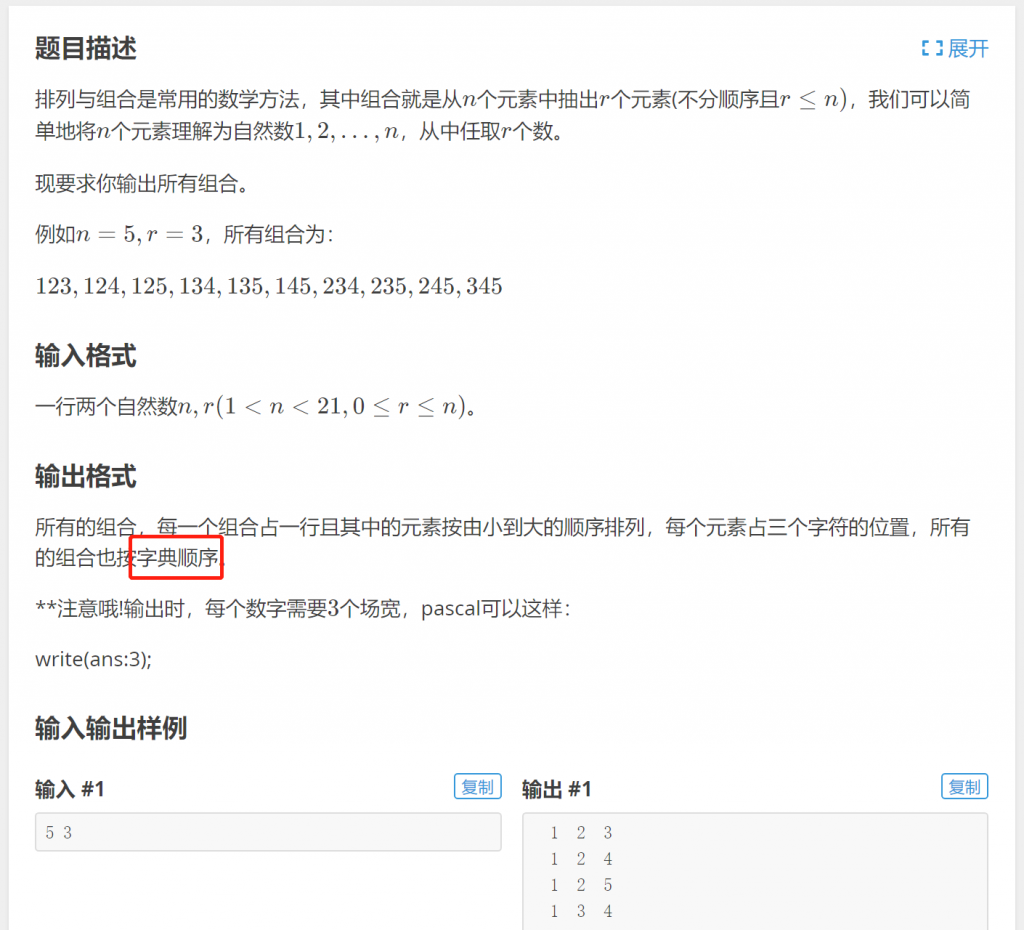
分析：这个问题看上去很简单，但是题目要求按照字典顺序输出，如果直接用上面策略不能保证输出的组合符合字典顺序：

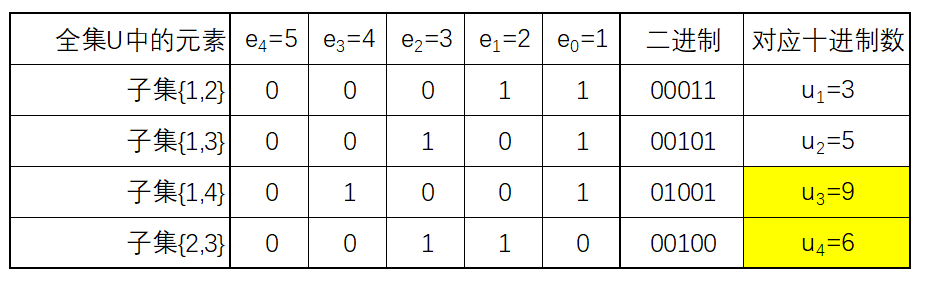
由上面表格分析可知，如果按照 0～(2<<n)-1 升序依次枚举子集，那么子集 {2,3}（对应十进制数 6）会在{1,4}（对应十进制数 9）之前输出，不符合字典顺序。如果我们将元素 1 是否存在放在二进制的最高位，元素 2 是否存在放在二进制的次高位……，如下图所示：

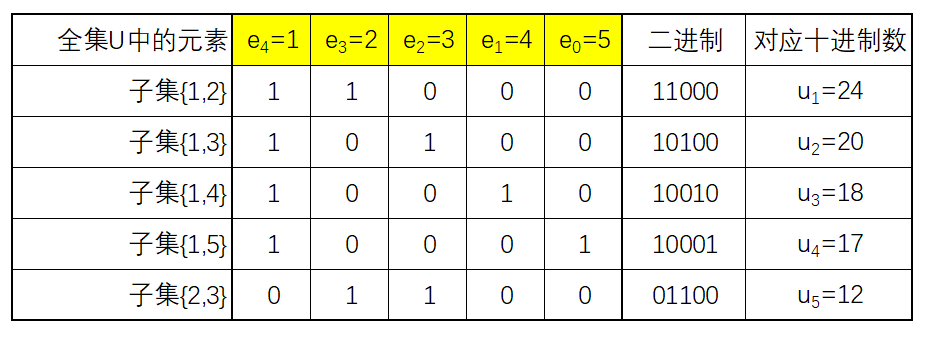
可以发现此时如果按照 (2<<n)-1～0 降序依次枚举子集，那么输出的子集情况可以满足字典顺序：

#include<iostream>
using namespace std;
int e[20];
int main()
{
    int n,m;
    cin>>n>>m;

    //数字n,n-1,...,3,2,1从大到小依次存入数组（全集元素）
    for(int i=0;i<n;i++) e[i] = n-i;

    //逆序枚举每一个子集（对应的十进制数）
    for(int S=(1<<n)-1;S>=0;S--){
        if(__builtin_popcount(S)!=m) continue;
        //依次判断整数1,2,...,n（存储在e[n-1]、e[n-2]、...、e[0]）是否在子集S中
        for(int i=n-1;i>=0;i--){
            if(S&(1<<i)) cout<<e[i]<<" ";
        }
        cout<<endl;
    }
    return 0;
}

上述枚举子集算法的时间复杂度是 $O(2^n)$（两个示例程序的时间复杂度是 $O(n*2^n)$），一般情况下 1s 内可以枚举元素数量为 20～30 的集合的子集。枚举子集时如果对顺序有要求，需要确定枚举的方向和用二进制描述全集时二进制每一位标记的元素。