排列枚举

排列枚举，就是枚举所有元素的排列（要考虑元素的先后顺序）情况。例如三个数 {1,2,3} 的所有排列情况有：{1,2,3}，{1,3,2}，{2,1,3}，{2,3,1}，{3,1,2}，{3,2,1}一共 6 种情况。 四个数{1,2,3,4} 的所有排列情况有：{1,2,3,4}、{1,2,4,3}、{1,3,2,4}、{1,3,4,2}、{1,4,2,3}、{1,4,3,2}、{2,1,3,4}、{2,1,4,3}、{2,3,1,4}、{2,3,4,1}、{2,4,1,3} 、{2,4,3,1}、{3,1,2,4}、{3,1,4,2}、{3,2,1,4}、{3,2,4,1}、{3,4,1,2}、{3,4,2,1}、{4,1,2,3}、{4,1,3,2}、{4,2,1,3}、{4,2,3,1}、{4,3,1,2}、{4,3,2,1} 一共 24 种情况。

下面的四重循环程序可以输出四个数{1,2,3,4} 的所有排列：

#include<iostream>
using namespace std;
int main(){
	int cnt = 0;
    for(int i1=1;i1<=4;i1++){				//枚举第一个数 
    	for(int i2=1;i2<=4;i2++){			//枚举第二个数
			//第二个数不能和第一个数重复 
    		if(i2==i1) continue; 
    		for(int i3=1;i3<=4;i3++){		//枚举第三个数
				//第三个数不能和前两个数重复 
    			if(i3==i1 || i3==i2) continue; 
    			for(int i4=1;i4<=4;i4++){	//枚举第四个数
    				//第四个数不能和前三个数重复 
    				if(i4==i1 || i4==i2 || i4==i3) continue;
    				cout<<"{"<<i1<<","<<i2<<","<<i3<<","<<i4<<"} ";
    				cnt++;
    			}
    		}
		}
	}
	cout<<endl<<cnt<<endl;
    return 0;
}

如果要输出四个数{1,2,3,4} 选三个数的所有排列，只需要三重循环枚举选出来的两个数即可：

//四选三排列
#include<iostream>
using namespace std;
int main(){
	int cnt = 0;
    for(int i1=1;i1<=4;i1++){				//枚举第一个数 
    	for(int i2=1;i2<=4;i2++){			//枚举第二个数
			//第二个数不能和第一个数重复 
    		if(i2==i1) continue; 
    		for(int i3=1;i3<=4;i3++){		//枚举第三个数
				//第三个数不能和前两个数重复 
    			if(i3==i1 || i3==i2) continue; 
    			cout<<"{"<<i1<<","<<i2<<","<<i3<<"} ";
    			cnt++; 
    		}
		}
	}
	cout<<endl<<cnt<<endl;
    return 0;
}

注意对比和前面四选三组合情况程序的区别：

//四选三组合
#include<iostream>
using namespace std;
int main(){
    for(int i1=1;i1<=2;i1++){
        for(int i2=i1+1;i2<=3;i2++){
            for(int i3=i2+1;i3<=4;i3++){
                cout<<i1<<" "<<i2<<" "<<i3<<endl;
            }
        }
    }
    return 0;
}

如果是更多的数的全排列，用上面的多重循环实现过于复杂。进一步，如果数的数量是一个变量，是无法用多重循环处理的。

其实 \(n\) 个元素的全排列一共有 \(n!\) 种的情况，所以枚举 \(n\) 个元素全排列的算法的时间复杂度是 \(O(n!)\)。这里介绍STL（标准模板库）中的一个函数 next_permutation 来实现全排列枚举，后面我们还可以使用搜索算法来实现更普遍的排列枚举。

next_permutation 函数的功能很强大，其使用方法和sort函数类似：next_permutation(a,a+n)，实现的功能是调整数组a[0]~a[n-1]元素的位置以更换成下一个排列形式，注意这里是每调用一次更换成下一个排列。例如数组a初始元素是{1,2,3}，调用一次next_permutation(a,a+3)，数组a会变成{1,3,2}；再调用一次next_permutation(a,a+3)，数组a会变成{2,1,3}。并且next_permutation函数有返回值，当没有下一个排列的时候会返回 false。

来看例题：P1706 全排列问题

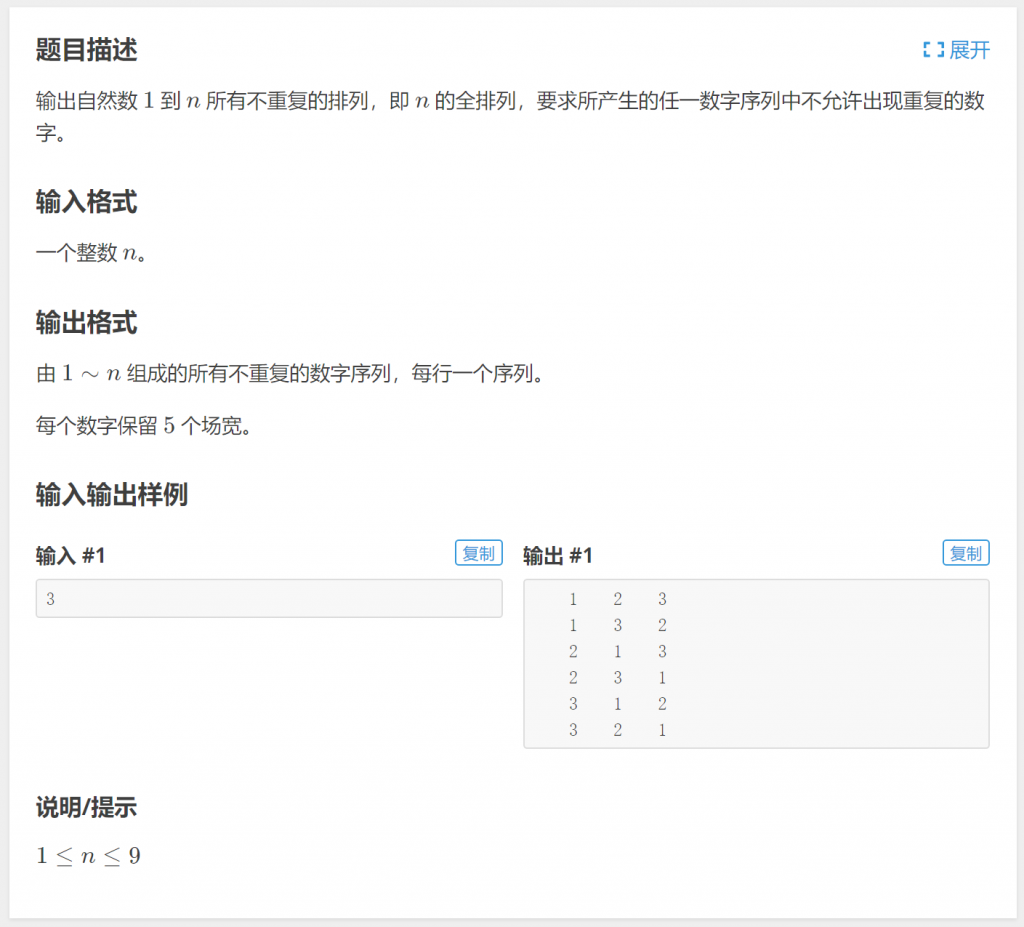
将1~n存入到数组中，通过反复调用 next_permutation 函数直到其返回值为 false 为止，每调用一次输出数组中的元素即可。考虑到数组初始状态也是一种排列形式，所以这里使用 do...while 循环：

#include<bits/stdc++.h>
using namespace std;
int a[10];
int main()
{
	int n;
	scanf("%d",&n);
	for(int i=0;i<n;i++) a[i] = i+1;
	do{
		for(int i=0;i<n;i++) printf("%5d",a[i]);
		printf("\n");
	}while(next_permutation(a,a+n));
    return 0;
}

来看下面的例子，会发现 next_permutation 函数在处理过程中如果发现数组中的元素是非下降排列的时候，就认定没有其他排列了，此时函数的返回值是false。所以如果要遍历所有的排列情况，可以在 do...while 循环前先对数组中的元素按升序排序处理：

#include<iostream>
#include<algorithm>
using namespace std;
int a[5] = {5,4,3,2,1}; 
int main()
{
    do{
    	for(int i=0;i<5;i++)
			cout<<a[i]<<" ";
    	cout<<endl;
	}while(next_permutation(a,a+5));
    return 0;
}

#include<iostream>
#include<algorithm>
using namespace std;
int a[5] = {5,4,3,2,1}; 
int main()
{
	sort(a,a+5);
    do{
    	for(int i=0;i<5;i++)
			cout<<a[i]<<" ";
    	cout<<endl;
	}while(next_permutation(a,a+5));
    return 0;
}

当要进行全排列的数中有重复的数时， next_permutation 函数可以自动实现排列情况不重复。

#include<bits/stdc++.h>
using namespace std;
const int N = 4;
int a[N] = {1,2,2,2};
int main()
{
	
    do{
        for(int i=0;i<N;i++)
			printf("%5d",a[i]);
        printf("\n");
    }while(next_permutation(a,a+N));
    return 0;
}

    1    2    2    2
    2    1    2    2
    2    2    1    2
    2    2    2    1

其实前面解决的“P1618 三连击（升级版）”也可以使用排列枚举来处理，时间复杂度是\(O(9!)\)，1s内可以处理完毕：

#include<bits/stdc++.h>
using namespace std;
int a[10];
int main()
{
	int A,B,C,x,y,z,cnt=0;
	cin>>A>>B>>C;
	for(int i=1;i<=9;i++) a[i] = i;
	do{
		x = a[1]*100+a[2]*10+a[3];
		y = a[4]*100+a[5]*10+a[6];
		z = a[7]*100+a[8]*10+a[9];
		if(x*B==y*A && x*C==z*A){       //不用除法避免浮点数误差
			cout<<x<<" "<<y<<" "<<z<<endl;
			cnt++;
		}
	}while(next_permutation(a+1,a+10));
	if(cnt==0) cout<<"No!!!"<<endl;
    return 0;
}

再来看例题：P1088 火星人

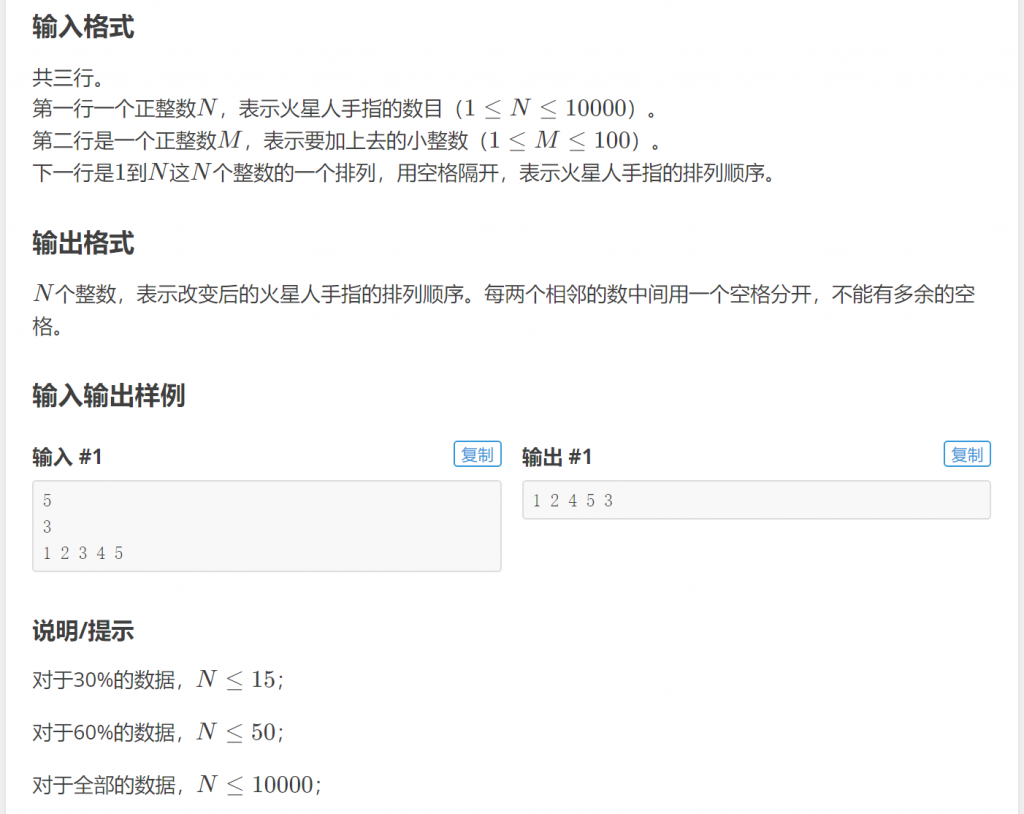
仔细分析题意会发现问题求解的是\(n\)个元素第\(m\)个排列情况，使用next_permutation函数可以让程序变得很简洁高效：

#include<bits/stdc++.h>
using namespace std;
int a[10001],n,m;
int main(){
    cin>>n>>m;
    for(int i=0;i<n;i++) cin>>a[i];
    for(int i=0;i<m;i++) next_permutation(a,a+n);
    for(int i=0;i<n;i++) cout<<a[i]<<" ";
    return 0;
}

需要注意的是，枚举所有排列情况的算法时间复杂度是\(O(n!)\)，一般情况下在1s内很难枚举超过11个元素的全排列！使用排列枚举要特别关注问题规模，避免超时！