递推算法（1）——基础

递推算法是一种重要的数学方法，在数学领域广泛应用，也是计算机领域用于数值计算的一种重要算法。递推算法的特点是：一个问题的求解需要一系列的计算，在已知条件和所求问题之间存在着某种相互联系的关系，在计算时，如果能够找到前后过程之间的数量关系（也就是递推式），那么可以由已知条件出发逐步推导得出问题答案。

递推算法的首要问题是得出相邻的数据项间的关系，也就是递推关系。这样可以避免求数学通项公式的麻烦，把复杂问题的求解，分解成连续的若干步简单计算。这里类似于高中数学数列知识中的通项公式和递推公式。

递推算法经典问题就是前面介绍过的斐波那契数列。斐波那契数列可以描述为数列的第1项、第2项都是1，从第3项开始，每一项是前面两项的和。用数学递推公式可以描述为：

\( F_n=\left\{ \begin{aligned} 1(n=1,2) \\ F_{n-1}+F_{n-2}(n>=3) \end{aligned} \right. \)

如果将斐波那契数列存储到数组 f 中，那么初始值是 f[1]=f[2]=1，递推式是 f[n]=f[n-1]+f[n-2]。

#include<iostream>
using namespace std;
long long f[93] = {0,1,1};  //数组元素部分赋值 
int main()
{
    int n;
    cin>>n;
    for(int i=3;i<=n;i++) f[i] = f[i-1]+f[i-2];
    for(int i=1;i<=n;i++) cout<<i<<":"<<f[i]<<endl;
    return 0;
}

例题：P1255 数楼梯

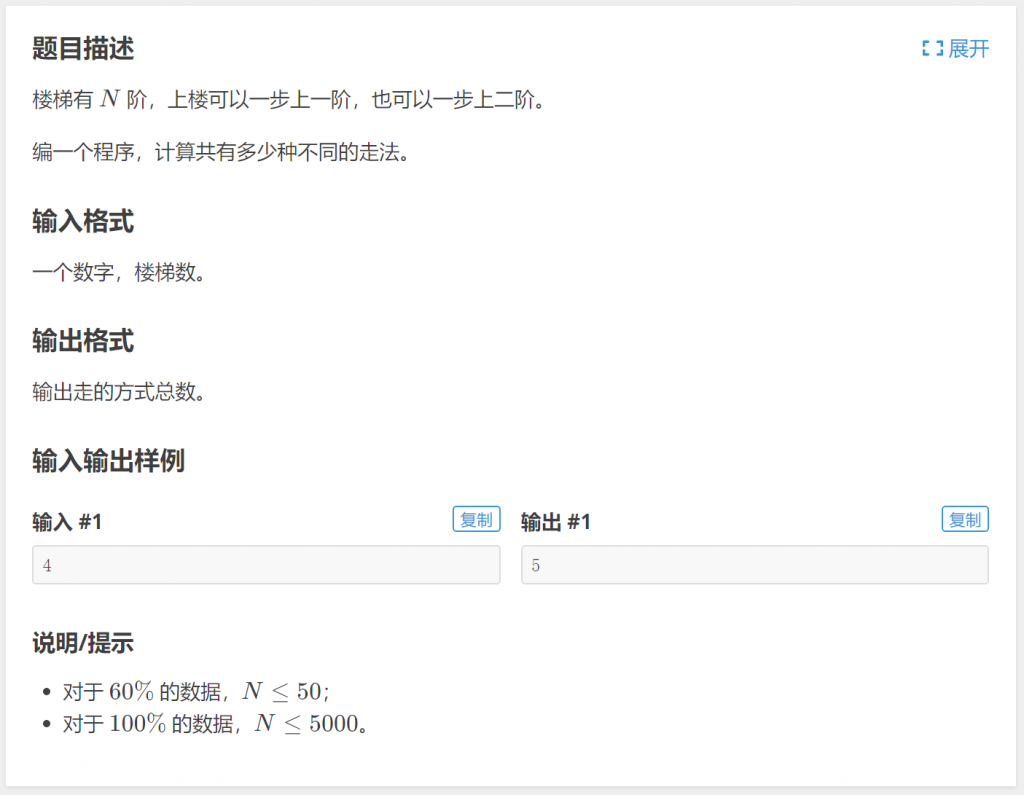
分析：假设\(n\)步台阶的走法总数是f[n]，那么\(n-1\)步台阶的走法总数是f[n-1]，\(n-2\)步台阶的走法总数是f[n-2]。

1. 如果现在走到了\(n-1\)步台阶，只需要再上一步，就能走到\(n\)步台阶，可知对于每一种走到\(n-1\)步台阶的方法都对应了一种走到\(n\)步台阶的方法；
2. 如果现在走到了\(n-2\)步台阶，在此基础上要走到\(n\)步台阶，有两种策略：
   1. 再上两步台阶，就能走到\(n\)步台阶，可知对于每一种走到\(n-2\)步台阶的方法此时都对应了一种走到\(n\)步台阶的方法；
   2. 上一步台阶，再上一步台阶（也就是连续两次上一步台阶）。仔细分析会发现，这样的走法和前面走到了\(n-1\)步台阶再上一步台阶的走法重复了。
3. 如果考虑其它走到更低台阶（例如走到了\(n-3\)步台阶）的基础上，继续上台阶走到\(n\)步台阶的情况，仔细分析会发现和前面的走法都重复。

通过上面的分析可知，f[n]只与f[n-1]和f[n-2]有关，并且f[n]=f[n-1]+f[n-2]，这就是求解问题的递推式（和斐波那契数列递推式一样），也很容易分析出初始值 f[1]=1,f[2]=2。

上面的分析过程展示了通过理论推导求递推式的过程，实际解决问题时，往往不能很容易想到这样的理论推导过程，那么可以通过笔算1步、2步、3步、4步、5步（设置更多）台阶的走法数，通过这些笔算结果找规律来得出递推公式。但最好要对通过找规律得出的递推公式加以严谨的数学论证。

考虑问题规模，这里应该使用高精度整数来实现求和递推计算：

#include<iostream>
using namespace std;
int f[5010][2010];    //存储每一项都是高精度数的递推序列
int main()
{
	int n;
	cin>>n;
	f[0][0] = 1,f[0][1] = 0;	//第0项，高精度是0（过输入0的测试点） 
    f[1][0] = f[1][1] = 1;	  //第1项，高精度数1 
    f[2][0] = 1,f[2][1] = 2;	//第2项，高精度数2
	for(int i=3;i<=n;i++){
		int x = 0;
		for(int j=1;j<=f[i-1][0] || j<=f[i-2][0];j++){
			f[i][0]++;
			f[i][j] = f[i-1][j] + f[i-2][j] + x;
			if(f[i][j]>=10) f[i][j] -= 10,x = 1;
			else x = 0;
		}
		if(x) f[i][++f[i][0]] = x;
	}
	for(int i=f[n][0];i>=1;i--) cout<<f[n][i];
    return 0;
}

上面代码中全局二维数组用来存储每一项都是高精度数的递推序列，这个数组的第一维度长度根据问题规模很容易确定，第二维度开多大如何确定呢？其实最简单的方法是先开一个较大的，例如int f[5010][10010];，跑一下输入最大值5000，通过结果就能确定序列最大值高精度数的位数，这样就能确定第二维的长度了（测试发现序列第5000项的高精度数的位数是1045，所里这里第二维开到1046就行）。如果真的开到int f[5010][10010];这么大的数组，会出现部分测试点内存超出限制的错误。

例题：骨牌问题

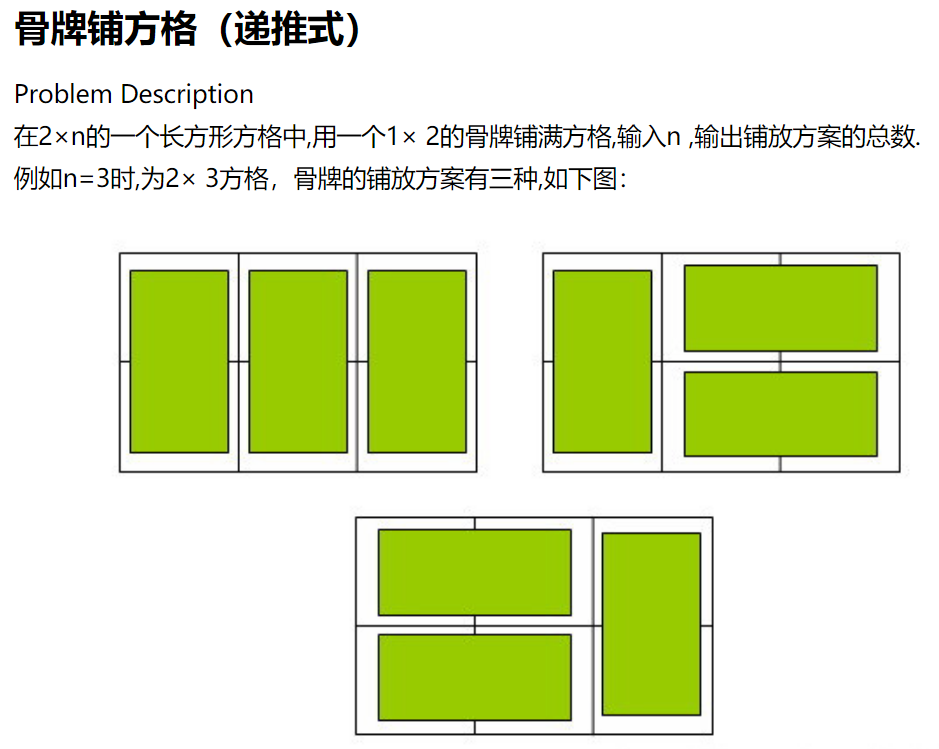
这也是一个典型的斐波那契数列递推式，和上面的爬楼梯结果完全一致，读者可以自行画图分析f[n]与f[n-1]和f[n-2]的关系。

例题：昆虫繁殖

有一种昆虫，昆虫的卵需要 2 个月才能长成成虫，每对卵长成成虫 \(x\) 个月后每月产 \(y\) 对卵。假设每对成虫不死，第一个月只有一对刚由卵长成的成虫，问 \(z\) 个月后有多少对成虫？输入 \(x,y,z\) 的值，计算并输出 \(z\) 个月后成虫的对数。

分析：可以使用两个数组来分别记录成虫和卵的对数，借助循环递推结果：

#include<iostream>
using namespace std;
long long a[101],b[101];
int main()
{
    int x,y,z;
    cin>>x>>y>>z;

    //第1个月到第x个月，只有一对成虫，没有虫卵 
    for(int i=1;i<=x;i++) a[i]=1,b[i]=0;

    for(int i=x+1;i<=z+1;i++){   //z个月后 
    	b[i] = y*a[i-x];		 //虫卵对数（x月前的成虫均能产卵）
    	a[i] = a[i-1]+b[i-2];	//上个月成虫+经过2个月长成的成虫（2个月前的卵） 
	} 
	cout<<a[z+1]<<endl; 
    return 0;
}

例题：P1011 车站

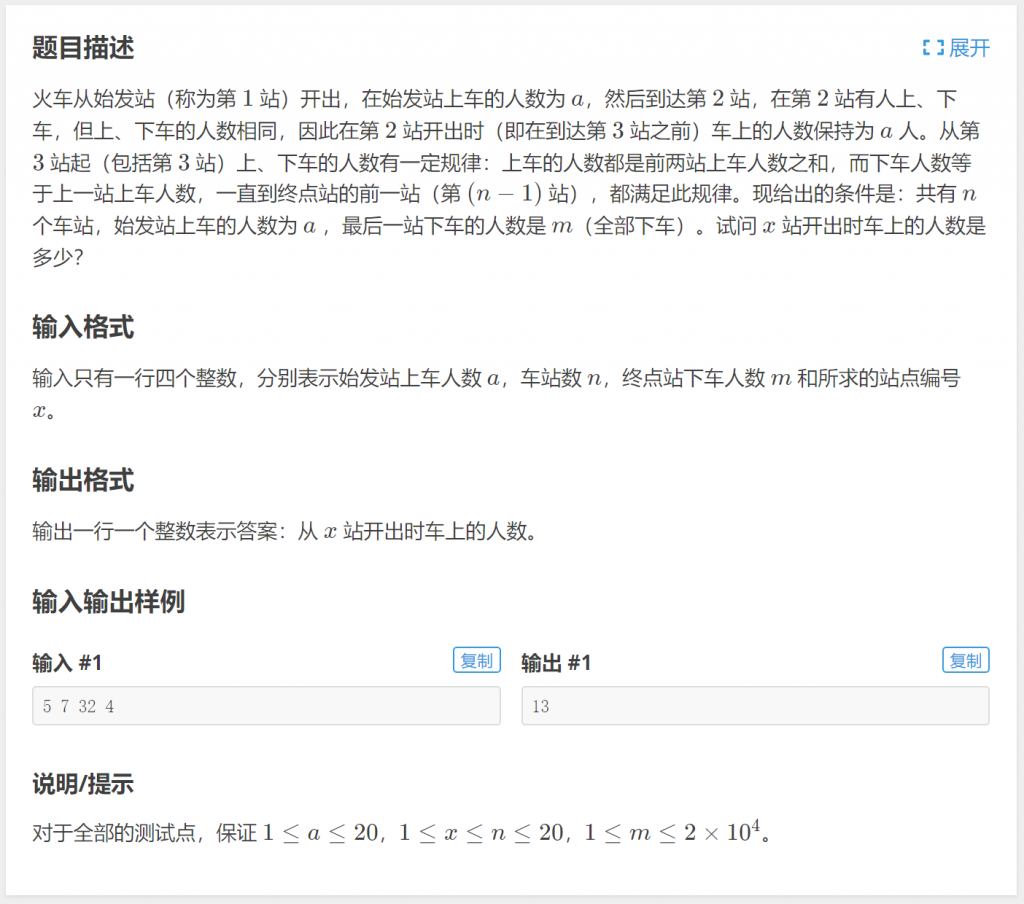
分析：可以直接模拟递推整个过程，但是题目没有提供第2站上车人数（求第2站上车人数是问题的一个关键点），所以无法直接递推下去，那么不妨假设第2站上车人数为\(b\)，通过列表来分析问题：

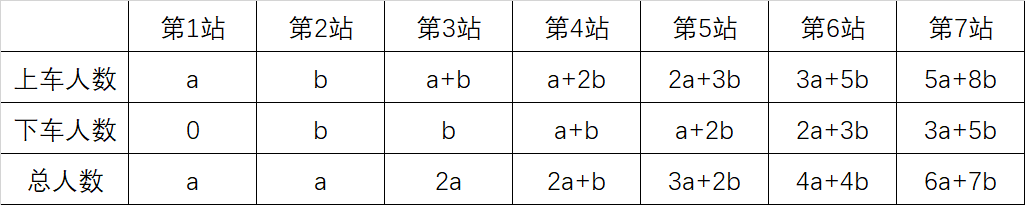
分析表格（其实分析题意也可以）会发现，第 \(i\) 站开出时人数 f[i] 与第 \(i-1\) 站开出时人数 f[i-1] 和第 \(i-2\) 站上车人数 up[i-2] 有关：f[i]=f[i-1]+up[i-2]\((i \ge 3)\)。因为从第 3 站起，上车的人数都是前两站上车人数之和，而下车人数等于上一站上车人数，那么上车人数与下车人数之差是【上上站的上车人数】，也是这一站开出时比上一站增加的人数。

现在来分析第 \(i\) 站上车人数 up[i]，观察表格可知 up[i] 可以描述为 \(upa[i] \times a + upb[i] \times b\) 这样的算式，可以通过递推得出 \(a\) 的系数 \(upa[i]\) 依次是 {1,0,1,1,2,3,5,...}，\(b\) 的系数 \(upb[i]\) 依次是 {0,1,1,2,3,5,8,...}，都是典型的斐波那契数列（upa[i] = upa[i-1]+upa[i-2]，upb[i] = upb[i-1]+upb[i-2]）。那么第 \(i\) 站开出时人数 f[i] 也可以描述为 \(a\)、\(b\) 的系数：\(fa[i] \times a + fb[i] \times b\)。由f[i]=f[i-1]+up[i-2]，可以得出系数的递推式：fa[i] = fa[i-1]+upa[i-2]，fb[i] = fb[i-1]+upb[i-2]。

第 \(n\) 站所有人都下车，下车人数为 \(m\)，其实就是第 \(n-1\) 站开出时人数为 \(m\)。可以由递推得出的第 \(n-1\) 站开出时人数 \(fa[n-1] \times a + fb[n-1] \times b=m\)，计算出 \(b\)，就可以直接套用系数计算第 \(x\) 站开出时人数：

#include<iostream>
using namespace std;
//第i站上车人数：upa[i]*a+upb[i]*b，upa数组记录a的系数，upb数组记录b的系数
long long upa[21] = {0,1,0};
long long upb[21] = {0,0,1};
//第i站开出时人数：fa[i]*a+fb[i]*b，fa数组记录a的系数，fb数组记录b的系数
long long fa[21] = {0,1,1};
long long fb[21] = {0,0,0};
int main()
{
    int a,b,n,m,x;
    cin>>a>>n>>m>>x;
    for(int i=3;i<=n-1;i++){
    	upa[i] = upa[i-1]+upa[i-2];
    	upb[i] = upb[i-1]+upb[i-2];
    	
    	fa[i] = fa[i-1]+upa[i-2];
    	fb[i] = fb[i-1]+upb[i-2];
	}
	b = (m-fa[n-1]*a)/fb[n-1];
	cout<<fa[x]*a+fb[x]*b<<endl;
    return 0;
}

进一步分析会发现，第 \(i\) 站开出时人数 f[i] 描述为 \(a\)、\(b\)的系数：\(fa[i] \times a + fb[i] \times b\)：

那么可以省去计算上车人数的过程：

#include<iostream>
using namespace std;
//第i站开出时人数：fa[i]*a+fb[i]*b，fa数组记录a的系数，fb数组记录b的系数
long long fa[21] = {0,1,1,2};
long long fb[21] = {0,0,0,0};
int main()
{
    int a,b,n,m,x;
    cin>>a>>n>>m>>x;
    for(int i=4;i<=n-1;i++){        
        fa[i] = fa[i-1]+fa[i-2]-1;
        fb[i] = fb[i-1]+fb[i-2]+1;
    }
    b = (m-fa[n-1]*a)/fb[n-1];
    cout<<fa[x]*a+fb[x]*b<<endl;
    return 0;
}