本文通过几个经典的例题介绍几种典型的递推关系。在实际做题时,如果找不出递推关系,那么可以尝试笔算得出前几项结果,通过寻找规律来发现递推关系。严格情况下,通过寻找规律得出的递推关系需要进一步理论论证。
1.斐波那契数列
来看兔子繁殖问题:一般而言,兔子在出生两个月后,就有繁殖能力,一对兔子每个月能生出一对小兔子来。如果所有兔子都不死,那么一对兔子经过一年繁殖以后,一共有多少对兔子?
假设满 \(n\) 个月后共有兔子 \(F_n\) 对,那么满 \(n-1\) 个月后兔子数量可以表示为 \(F_{n-1}\) 对。由题意可知第 \(n\) 月新生的小兔子数量和第 \(n-2\) 月的兔子总数相等(\(F_{n-2}\) 对)。满 \(n\) 个月后的兔子是由满 \(n-1\) 个月后兔子外加第 \(n\) 月新生的小兔子组成的,那么可知:
\(F_n = F_{n-1}+F_{n-2}\),初始值:\(F_1 = F_2 = 1\)
其实斐波那契数列有通项公式:
\(F_n=\frac{\sqrt5}{5}\left[\left(\frac{1+\sqrt5}{2}\right)^n-\left(\frac{1-\sqrt5}{2}\right)^n\right]\\\)
值得一提的是,斐波那契数列是自然数的数列,但其通项公式却是用无理数来表达的。
2.汉诺塔问题
汉诺塔(\(\verb|Hanoi Tower|\)),又称河内塔,源于印度一个古老传说。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着 64 片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,任何时候,在小圆盘上都不能放大圆盘,且在三根柱子之间一次只能移动一个圆盘。问至少需要移动多少次?
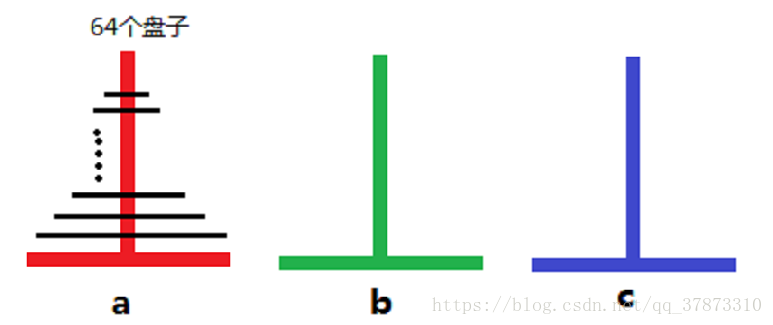
可以将问题简化成如下图所示的模型,64 个从小到大依次重叠的盘子需要从 a 柱子移动到 c 柱子上,移动的过程中可以临时放在 b 柱子上,并且移动规则如下:
- 一次只能移动一个盘子
- 盘子只能放在 a、b、c 三个柱子上
- 移动过程中只能小盘子压着大盘子,不能大盘子压着小盘子
假设将 \(n\) 个盘子从 a 柱子移动到 c 柱子需要 \(h_n\) 次,可知将 \(n-1\) 个盘子从 a 柱子移动到 c 柱子需要 \(h_{n-1}\) 次,同理可知将 \(n-1\) 个盘子从 a 柱子移动到 b 柱子需要 \(h_{n-1}\) 次、将 \(n-1\) 个盘子从 b 柱子移动到 c 柱子需要 \(h_{n-1}\) 次。
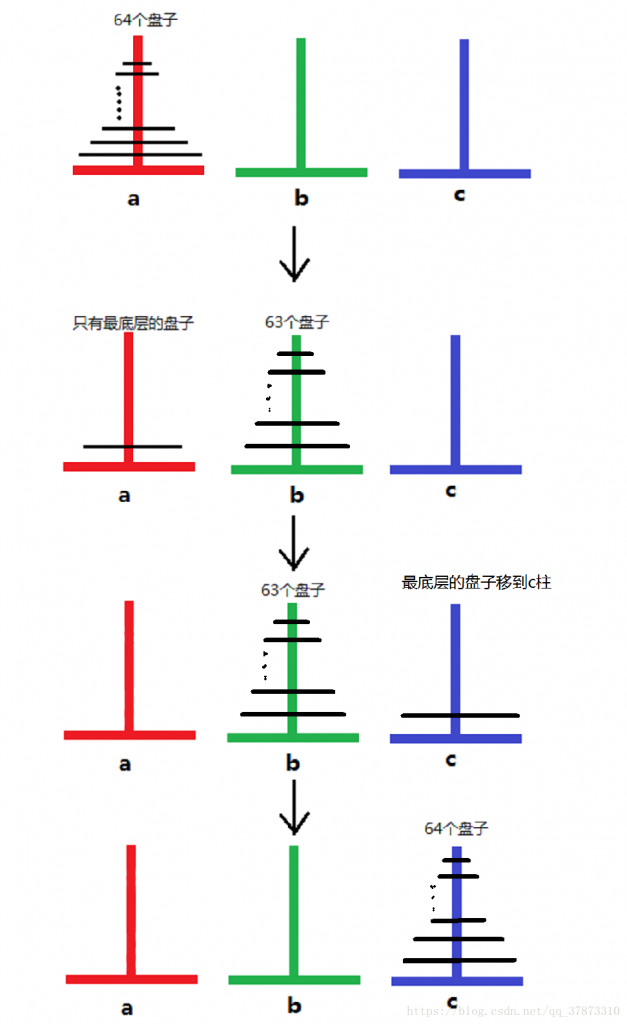
如果将 \(n\) 个盘子上面的 \(n-1\) 个盘子看成一个整体,那么移动的方案可以简单描述为:
- 想办法将看成整体的 \(n-1\) 个盘子借助 c 柱子过渡从 a 柱子移动到 b 柱子上,需要移动 \(h_{n-1}\) 次;
- 将 a 柱子上剩下的最大的盘子直接移动到 c 柱子上,仅需要 1 次;
- 想办法将看成整体的 \(n-1\) 个盘子借助 a 柱子过渡从 b 柱子移动到 c 柱子上,又需要移动 \(h_{n-1}\) 次。
通过上面分析可知汉诺塔问题递推公式为:
\(h_n=2h_{n-1}+1\),初始值:\(h_1 = 1\)
其实也能得出通项公式:\(h_n=2^n-1\)。
3.平面分割问题
1.直线分割平面问题
问题:\(n\) 条直线,最多可以将平面分割成多少区域?
问题考虑的是最多分割问题,那么 \(n\) 条直线必须两两相交,并且没有任意超过两条的直线相交于同一点,此时才能保证将平面分割的区域最多。假设满足这样的条件下,\(n\) 条直线将平面分成 \(f_n\) 个区域。
如果平面内已经有 \(n-1\) 条两两相交的直线,再添加一条直线与已有的 \(n-1\) 条直线相交。那么新添加的直线被分割成了 \(n\) 段,每一段将之前的 1 个区域一分为二,所以会新产生 \(n\) 个区域(建议自行画图分析)。
通过上面的分析可知问题的递推公式为:
\(f_n=f_{n-1}+n\),初始值:\(f_1 = 2\)
通过高中数学知识不难得出通项公式:\(f_n=\frac{n(n+1)}{2}+1\)。
2.椭圆分割平面问题
问题:有\(n\)条封闭曲线画在平面上,而任何两条封闭曲线恰好相交于两点,且任何三条封闭曲线不相交于同一点,问这些封闭曲线把平面分割成的区域个数。
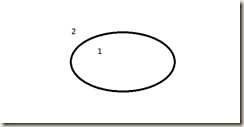
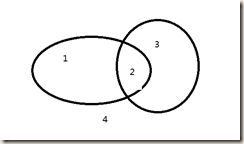
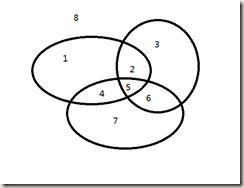
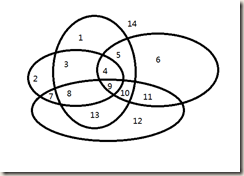
当有 \(n-1\) 个椭圆时,分割区域数为 \(f_{n-1}\),那么第 \(n\) 个椭圆就必须与前 \(n-1\) 个椭圆相交,则第 \(n\) 个椭圆被分为 \(2(n-1)\) 段,对应增加了 \(2(n-1)\) 个区域。
通过上面的分析可知问题的递推公式为:
\(f_n=f_{n-1}+2(n-1)\),初始值:\(f_1 = 2\)
通过高中数学知识能得出通项公式:\(f_n=n^2-n+2\)。
4.卡特兰数
来看问题:P1044 栈
原问题可以简化为:一个足够大的栈的进栈序列为 \(1,2,3,⋯,n\)时,有多少个不同的出栈序列。
假设 \(i\) 个不同的数一共有 \(h_i\) 种不同的出栈序列。考虑到每一个数都可能最后出栈,可以计算第 1 个数最后出栈时序列的总数,第 2 个数最后出栈时序列的总数,……,第 \(n\) 个数最后出栈时序列的总数,那么所求结果就是上述情况的总和。
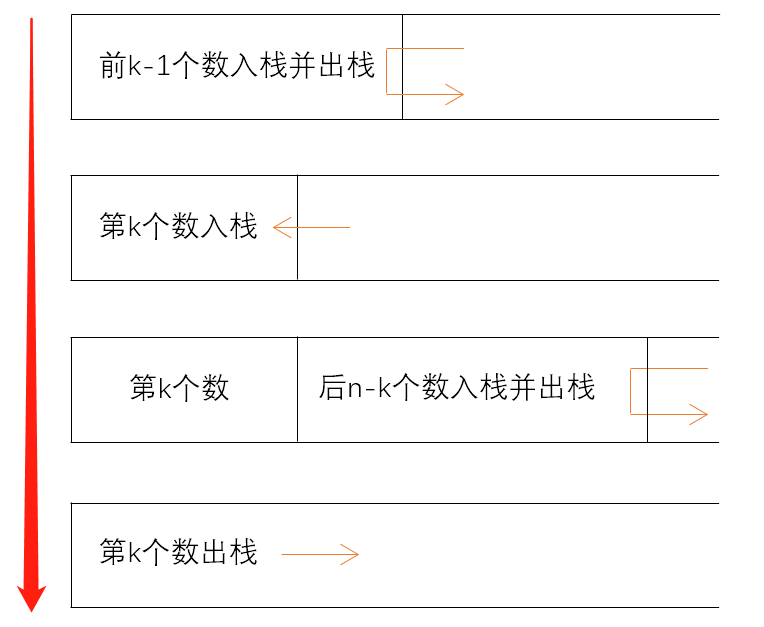
来看第 \(k\) 个数最后出栈的情况,可知前面有 \(k-1\) 个数已经入栈并出栈,一共有 \(h_{k-1}\) 种出栈序列;然后第 \(k\) 个数入栈;然后后面有 \(n-k\) 个数继续入栈并出栈,一共有 \(h_{n-k}\) 种出栈序列;最后第 \(k\) 个数出栈。整个序列是前面 \(k-1\) 个数入栈出栈产生的序列拼接上后面 \(n-k\) 个数入栈出栈产生的序列再拼接上第 \(k\) 个数产生的,那么第 \(k\) 个数最后出栈这种情况一共可以产生 \(h_{k-1}h_{n-k}\) 种出栈序列(乘法原理)。而 \(k\) 的取值可以是 1~\(n\),根据加法原理,整个问题的递推公式就是:
\(h_n=h_0h_{n-1}+h_1h_{n-2}+...+h_{n-1}h_0=\sum\limits_{i=0}^{n-1}h_ih_{n-i-1}\),初始值:\(h_0=h_1=1\)
#include<iostream>
using namespace std;
int h[20]={1,1};
int main()
{
int n;
cin>>n;
for(int i=2;i<=n;i++){
for(int j=0;j<i;j++){
h[i] += h[j]*h[i-j-1];
}
}
cout<<h[n]<<endl;
return 0;
}
上面递推公式产生的一系列数字称为卡特兰数。卡特兰数还是以下递推公式和通项公式:
\(h_i=h_{i-1} (4i-2)/(i+1)\) \(h_i=\frac{(2i)!}{i!(i+1)!}\)类似还有凸 \(n\) 边形内部不相交对角三角形的数量问题,也是卡特兰数(凸 \(n\) 边形内部不相交对角三角形的数量是卡特兰数的第 \(n-2\) 项)。读者可以查看这篇博文进一步了解卡特兰数:卡特兰数 — 计数的映射方法的伟大胜利。
5.第二类 \(\verb|stirling|\) 数
问题:\(n\) 个不同的球放到 \(m\) 个相同盒子里,要求没有空盒,问有多少种方案。
可以用 \(S_2(n,m)\) 来表示结果,称为“第二类 \(\verb|stirling|\) 数”,可以预见这个递推公式有 2 个参数。假设不同的球编号分别为 \(b_1,b_2,b_3,...,b_n\),从里面随意抽出一个编号为 \(b_i\) 的球,可知该球的放法有两种:
- 球 \(b_i\) 独占一个盒子,那么剩下的 \(n-1\) 个球只能放到剩下的 \(m-1\) 个盒子里,方案数有 \(S_2(n-1,m-1)\) 种;
- 球 \(b_i\) 与其它球共占一个盒子,那么可以先将其它 \(n-1\) 个球放在 \(m\) 个盒子里,然后再将球 \(b_i\) 放到其中一个盒子里,方案数为 \(mS_2(n-1,m)\) 种;
由此可知,第二类 \(\verb|stirling|\) 数的递推公式为:
\(S_2(n,m)=S_2(n-1,m-1)+mS_2(n-1,m)\)
初始值:\(S_2(n,0)=0,S_2(n,1)=1,S_2(n,n)=1,S_2(n,k)=0(k>n)\)
#include<iostream>
using namespace std;
long long S2[20][20];
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++){
S2[i][1] = 1;
for(int j=2;j<=m;j++){
S2[i][j] = S2[i-1][j-1]+j*S2[i-1][j];
}
}
cout<<S2[n][m]<<endl;
return 0;
}
来看问题“P1287 盒子与球”:\(n\) 个不同的球放到 \(m\) 个不同盒子里,要求没有空盒,求方案数。盒子不同,可以先将 \(m\) 个盒子排列后再按照上面的方法装球。根据高中数学排列知识可知,\(m\) 个盒子有 \(m!\) 种排列情况,最后的结果是:\(S_2(n,m) \times m!\)。
 NOIP学习小站
NOIP学习小站