本文通过例题来进一步帮助读者学习掌握递推算法。
一、位数问题
问题:在所有的 \(n\) 位数中,有多少个数中有偶数个数字 3?注意:如果一个数字没有出现 3,那么就有 0 个 3,也算有偶数个 3。由于结果很大,只需要输出答案对 12345 取余的值(\(1 \le n \le 1000\))。
分析:很显然,这里不能使用暴力求解。因为 \(n\) 位数可以由 \(n-1\) 位数在最高位添加一个数字得来,可以尝试使用递推算法。
- 如果 \(i-1\) 位数有偶数个 3,那么在最高位可以添加 0~2、4~9 这 9 个数字,得到仍然是偶数个 3 的 \(i\) 位数(要排除 \(i==n\) 时不能在最高位添加 0 的情况);
- 如果 \(i-1\) 位数有奇数个 3,那么在最高位添加上数字 3,得到是偶数个 3 的 \(i\) 位数。
可以用 \(e_i\) 表示 \(i\) 位数中有偶数个 3 的数字的个数,用 \(o_i\) 表示 \(i\) 位数中有奇数个 3 的数字的个数,那么有递推公式:
\(e_i=9e_{i-1}+o_{i-1}\),\(o_i=9o_{i-1}+e_{i-1}\)(i==n 时系数 9 要修正为 8)
初始值:\(e_1=9\)(1 位数中有 9 个数出现了 0 个 3),\(o_1=1\)
#include<iostream>
using namespace std;
int e[1010] = {0,9},o[1010] = {0,1};
int main()
{
int n;
cin>>n;
for(int i=2;i<=n;i++){
int x = 9;
if(i==n) x--; //最高位不能添加0,能添加的数的个数-1
e[i] = (x*e[i-1]+o[i-1])%12345;
o[i] = (x*o[i-1]+e[i-1])%12345;
}
cout<<e[n]<<endl;
return 0;
}
二、马拦过河卒
问题:P1002 过河卒

分析:可以先不考虑马的问题,过河卒可以向下,或者向右走,那么要走到坐标点 \((x,y)\),可以从坐标点 \((x-1,y)\) 向下走一步,也可以从坐标点 \((x,y-1)\) 向右走一步(注意图中坐标系)。如果将从坐标点 \((0,0)\) 到坐标点 \((x,y)\) 的走法数量记为 \(F(x,y)\),可知递推公式:
\(F(x,y)=F(x-1,y)+F(x,y-1)\),初始值:\(F(x,0)=F(0,y)=1\)
再来考虑有马的情况。有了马之后,那么马的控制点(包括马所在的那一点)过河卒不能走上去,可以直接将这些点特殊处理,走到这些点的路径数量设置为 0 即可。实际处理时,可以用二维数组来记录到每个坐标点的路径数量,并且将控制点的路径数量设置为一个特殊值 -1,这样可以减少一个标记控制点的数组:
#include<iostream>
using namespace std;
const int MAX = 25;
long long f[MAX][MAX];
int dirs[9][2] = {
{0,0},
{1,2},
{1,-2},
{-1,2},
{-1,-2},
{2,1},
{2,-1},
{-2,1},
{-2,-1}
};
int main()
{
int n,m,x,y;
cin>>n>>m>>x>>y;
//通过坐标变化数组dirs快速计算马的所有控制点
for(int i=0;i<9;i++){
int nx = x+dirs[i][0];
int ny = y+dirs[i][1];
//控制点,标记为特殊值-1
if(nx>=0 && nx<=n && ny>=0 && ny<=m) f[nx][ny]=-1;
}
f[0][0]++; //(0,0)如果是控制点变成0,否则是1
for(int i=0;i<=n;i++){
for(int j=0;j<=m;j++){
if(f[i][j]==-1) continue; //控制点,不处理
if(i && f[i-1][j]>0) f[i][j] += f[i-1][j]; //上边不是控制点
if(j && f[i][j-1]>0) f[i][j] += f[i][j-1]; //左边不是控制点
}
}
cout<<(f[n][m]==-1?0:f[n][m]);
return 0;
}
三、蜜蜂路线
问题:P2437 蜜蜂路线
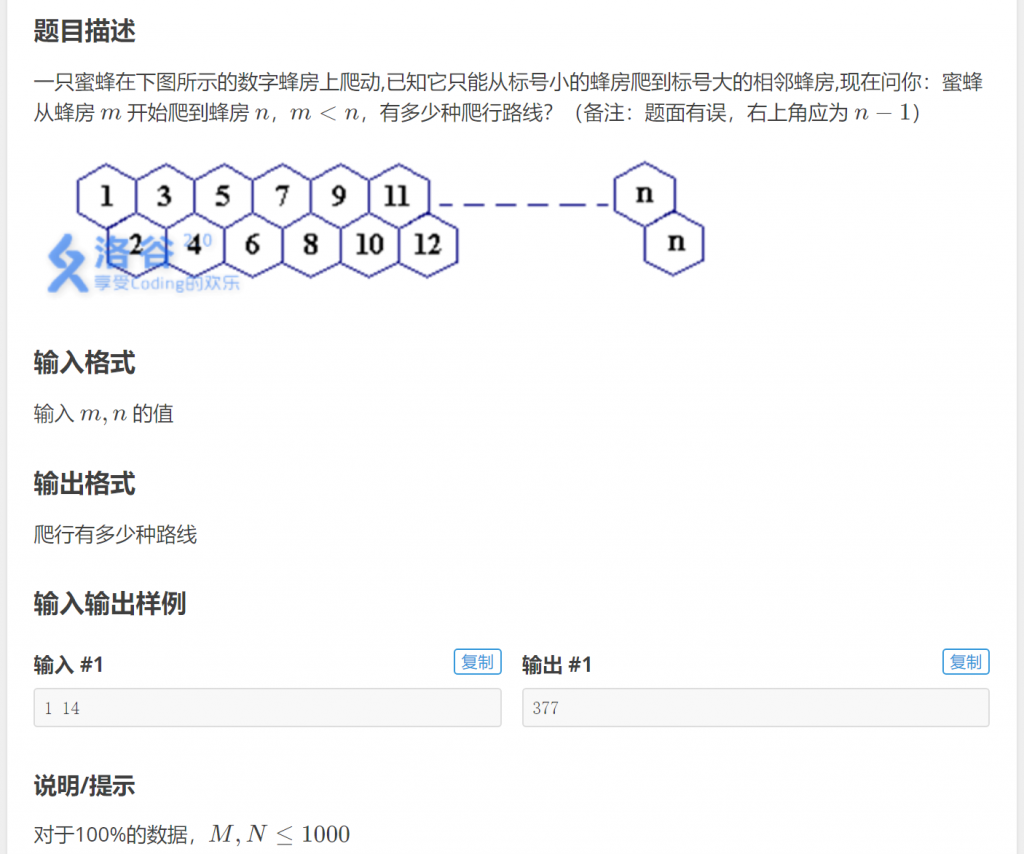
分析:先来看从编号 1 的蜂房爬到编号 \(i\) 的蜂房,可知只能从 \(i-1\) 或者 \(i-2\) 爬到 \(i\),那么从编号 1 的蜂房爬到编号 \(i\) 的蜂房的路线数量是从编号 1 的蜂房爬到编号 \(i-1\) 的蜂房和从编号 1 的蜂房爬到编号 \(i-2\) 的蜂房的路线数量的和。可以得出递推公式:
\(f_i=f_{i-1}+f_{i-2}\),初始值:\(f_1=f_2=1\)
其实从 \(m\) 爬到 \(n\),和从 1 爬到 \(n-m+1\) 的效果是一样的。所以要计算的是 \(f_{n-m+1}\),考虑到数据规模,需要用到高精度:
#include<iostream>
using namespace std;
int f[1010][220]={
{0},
{1,1}, //f[1]为高精度数1
{1,1} //f[2]为高精度数1
};
//高精度加法:a+b → c
void add(int a[],int b[],int c[]){
int x = c[0] = 0;
for(int i=1;i<=a[0]||i<=b[0];i++){
c[0]++;
c[i] = a[i]+b[i]+x;
if(c[i]>=10) c[i]-=10,x=1;
else x=0;
}
if(x) c[++c[0]] = x;
}
int main()
{
int m,n,t;
cin>>m>>n;
t = n-m+1;
for(int i=3;i<=t;i++){
add(f[i-1],f[i-2],f[i]);
}
for(int i=f[t][0];i>0;i--) cout<<f[t][i];
return 0;
}
 NOIP学习小站
NOIP学习小站