递归算法（1）

在函数学习时，已经初步学习了 递归函数 的使用，借助递归函数编写程序解决问题是一种重要的方法，能够使一些复杂的问题变得简单，对应地编写的程序也简洁。递归的特点是函数体中又调用自己。如果是直接调用自己称为直接递归；如果是函数 \(f\) 中调用函数 \(g\)，函数 \(g\) 中又调用函数 \(f\)，这样的递归称为间接递归。

一、从递推公式到递归函数

前面介绍递推的时候，对于问题都得出了递推公式，并且还有初始值。有了递推公式和初始值，可以很容易地写出对应的递归函数：递推公式就是递归调用的语句，初始值就是递归出口。

例如计算阶乘的递推公式是：

\(f_n=nf_{n-1}\)，初始值：\(f_1=1\)

那么递归函数可以写成：

#include<iostream>
using namespace std;
long long jc(int n){
	if(n==1) return 1;
	return n*jc(n-1);
}
int main()
{
	for(int i=1;i<=10;i++){
		cout<<i<<"!="<<jc(i)<<endl; 
	}
	return 0;
}

斐波那契数列的递推公式：

\(F_n = F_{n-1}+F_{n-2}\)，初始值：\(F_1 = F_2 = 1\)

递归函数可以写成：

#include<iostream>
using namespace std;
long long fib(int n){
	if(n==1 || n==2) return 1;
	return fib(n-1)+fib(n-2);
}
int main()
{
	for(int i=1;i<=10;i++){
		cout<<"fib("<<i<<")="<<fib(i)<<endl;
	}
	return 0;
}

第二类 \(\verb|stirling|\) 数的递推公式为：

\(S_2(n,m)=S_2(n-1,m-1)+mS_2(n-1,m)\)
初始值：\(S_2(n,0)=0,S_2(n,1)=1,S_2(n,n)=1,S_2(n,k)=0(k>n)\)

递归函数可以写成：

#include<iostream>
using namespace std;
long long S2(int n,int m){
	if(m==0) return 0;
	if(m==1) return 1;
	if(n==m) return 1;
	if(m>n) return 0;
	return S2(n-1,m-1)+m*S2(n-1,m);
}
int main()
{
	for(int i=1;i<=10;i++){
		for(int j=1;j<=i;j++){
			cout<<i<<"个不同的球,"<<j<<"个相同的盒子："<<S2(i,j)<<endl;
		}
	}
	return 0;
}

二、二分查找

来看递归实现二分查找问题：假设有 \(n\) 个整数已经按照从小到大排列，现在要查找整数 \(x\) 在序列中的位置。

最简单的方法当然是顺序查找，时间复杂度是 \(O(n)\)。如果 \(n\) 较大，会耗费不少时间，特别是要解决更复杂的问题时，如果将顺序查找置于循环体中，那么此时算法的时间复杂度是 \(O(n^2)\)。回到原问题，题目中给出了一个特殊的前提条件，那就是序列中的整数已经升序排列，可以借助二分查找来提高查找效率。

先来看一个简单的猜数字游戏，机器人从 1～15 中随机产生一个整数，要你来猜测这个数字，每次猜测后机器人会提供：猜对了、猜大了或者猜小了这样的反馈信息。如何快速猜出这个随机数？假设随机产生的整数是 11，可以这样猜测提高效率：

1. 首先猜测整个序列 [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15] 最中间的数字 8，机器人会反馈：猜小了；
2. 上一步反馈信息指出 8 比产生的随机数小，那么随机数肯定位于序列 [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15] 中数字 8 右边的部分 [9,10,11,12,13,14,15]。可以继续猜测这部分最中间的数字 12，机器人会反馈：猜大了；
3. 上一步反馈信息指出 12 比产生的随机数大，那么随机数肯定位于序列的 [9,10,11,12,13,14,15] 中数字 12 左边的部分 [9,10,11]。可以继续猜测这部分最中间的数字 10，机器人会反馈：猜小了；
4. 上一步反馈信息指出 10 比产生的随机数小，那么随机数肯定位于序列的 [9,10,11] 中数字 10 右边的部分 [11]。可以继续猜测这部分最中间的数字 11，机器人会反馈：猜对了。

通过分析可知，对于 \(n\) 个升序排列的数，采用上面的策略猜测（或者说查找），最多只需要 \(\log_2n\) 次就能得出结果，比起顺序查找，效率大大提升！

而上面的策略很简单，要在 \(n\) 个元素升序排列的数组 a 中查找元素 \(x\)，假设要查找序列第一个元素下标是 \(left\)，最后一个元素的下标是 \(right\)（此时 \(left=0,right=n-1\)）。问题可以描述为在升序数组 a 的 \(left→right\) 下标区域查找元素 \(x\)。可以找到最中间的下标 \(mid = (left+right)/2\)，然后按照下面的策略处理：

• 如果 \(a[mid]==x\)，可知找到元素 \(x\)；
• 如果 \(a[mid]<x\)，此时需要在 \(mid\) 的右边继续查找元素 \(x\)，问题转换为在数组 a 的 \(mid+1→right\) 下标区域查找元素 \(x\)；
• 如果 \(a[mid]>x\)，此时需要在 \(mid\) 的左边继续查找元素 \(x\)，问题转换为在数组 a 的 \(left→mid-1\) 下标区域查找元素 \(x\)；

要在 \(left→right\) 下标区域查找元素 \(x\)，现在分解成了在更小范围的“在 \(mid+1→right\) 下标区域查找元素 \(x\)”或者“在 \(left→mid-1\) 下标区域查找元素 \(x\)”这两个与原问题本质相同的子问题。同样的，在 \(mid+1→right\) 下标区域查找元素 \(x\) 又可以按照这样的方法分解成在两个更小范围的下标区域查找元素 \(x\) 的本质相同的子问题。这样一直分解下去，直到分解所得的下标区域不合理为止（开始下标大于结束下标）。

如果设计一个函数 search(int a[],int left,int right,int x)，用来实现在元素升序排列的数组 a 的 \(left→right\) 下标区域查找元素 \(x\)，那么分解出来的子问题同样可以调用这个函数来处理，这是很明显的递归调用，这样借助递归解决问题的思路称为递归思想。

#include<iostream>
using namespace std;
//在元素升序排列的数组a的left→right下标区域查找元素x
//找到返回元素x的下标，找不到返回特殊值-1
int search(int a[],int left,int right,int x){
	if(left>right) return -1;
	int mid = (left+right)/2;

	if(a[mid]==x) return mid;
	if(a[mid]<x) return search(a,mid+1,right,x);
	return search(a,left,mid-1,x);
}
int main()
{
	int arr[15] = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15};
	cout<<search(arr,0,14,11)<<endl;
	return 0;
}

如果查找的 \(x\) 在数组中重复出现时要求返回最小的下标，还需要对递归函数进行调整：

#include<iostream>
using namespace std;
//在元素升序排列的数组a的left→right下标区域查找元素x
//找到返回元素x的下标，找不到返回特殊值-1
//查找的x在数组中重复出现时要求返回最小的下标 
int search(int a[],int left,int right,int x){
    if(left>right) return -1;
    if(a[left]==x) return left;    //开始下标left的值就是x，找到了值为x的最小下标
    int mid = (left+right)/2;

    //a[mid]==x，在left→mid中查找元素x，保证找到的x是下标最小的 
    if(a[mid]==x) return search(a,left,mid,x);
    if(a[mid]<x) return search(a,mid+1,right,x);
    return search(a,left,mid-1,x);
}
int main()
{
    int arr[15] = {1,2,3,4,5,6,7,8,9,11,11,12,13,14,15};
    cout<<search(arr,0,14,11)<<endl;
    return 0;
}

三、汉诺塔问题

汉诺塔（\(\verb|Hanoi Tower|\)），又称河内塔，源于印度一个古老传说。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着 64 片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，任何时候，在小圆盘上都不能放大圆盘，且在三根柱子之间一次只能移动一个圆盘。问要做到移动次数最少，该如何移动？输出具体的移动方案。

可以将问题简化成如下图所示的模型，64 个从小到大依次重叠的盘子需要从 a 柱子移动到 c 柱子上，移动的过程中可以临时放在 b 柱子上，并且移动规则如下：

• 一次只能移动一个盘子
• 盘子只能放在 a、b、c 三个柱子上
• 移动过程中只能小盘子压着大盘子，不能大盘子压着小盘子

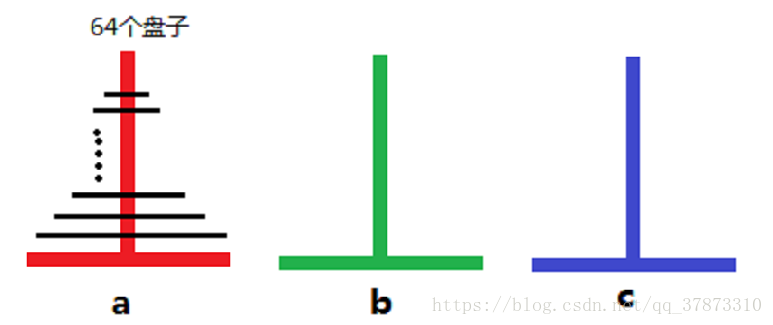
原问题可以归纳为：将 \(n\) 个盘子借助 b 柱子过渡从 a 柱子移动到 c 柱子上。如果将 \(n\) 个盘子上面的 \(n-1\) 个盘子看成一个整体，那么移动的方案可以简单描述为：

1. 想办法将看成整体的 \(n-1\) 个盘子借助 c 柱子过渡从 a 柱子移动到 b 柱子上；
2. 将 a 柱子上剩下的最大的盘子直接移动到 c 柱子上；
3. 想办法将看成整体的 \(n-1\) 个盘子借助 a 柱子过渡从 b 柱子移动到 c 柱子上。

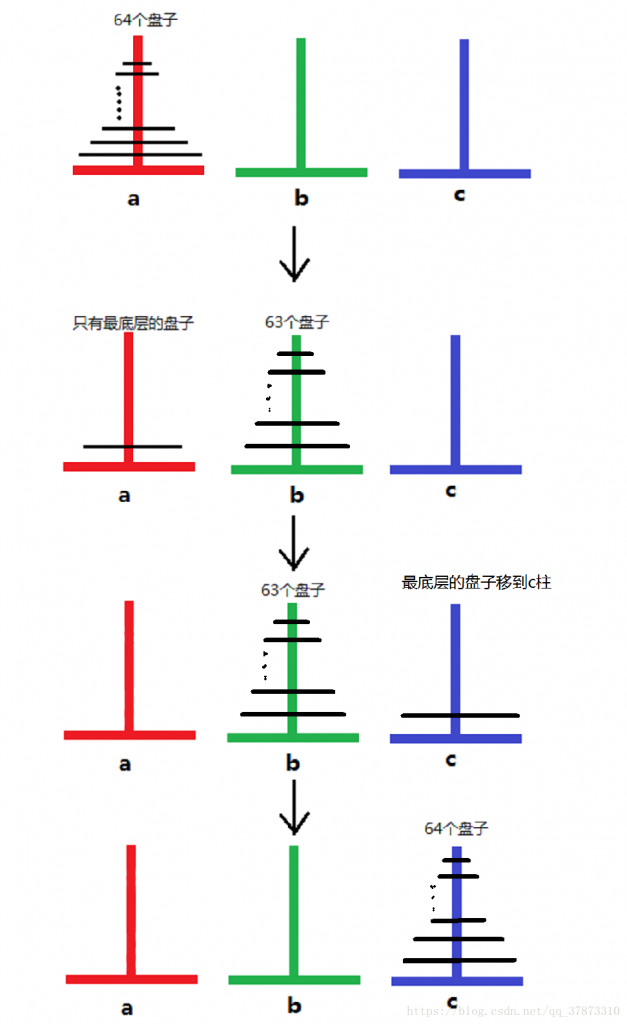
那么如何具体移动前面看成一个整体的 \(n-1\) 个盘子呢？这里又可以将上面的 \(n-2\) 个盘子看成一个整体，还是按照上面的策略移动。同样的还可以一直划分下去，直到整个柱子上没有盘子为止。这里可以设计一个函数 void hanoi(int n,char A,char B,char C); 用来实现将 \(n\) 个在 A 柱子上的盘子，借助 B 柱子过渡，最终移动到 C 柱子上，可见上面的盘子移动策略的第 1 、3 两步都是与原问题本质相同的问题，都能递归调用这个函数实现。根据上面的分析能够写出递归函数：

#include<iostream>
using namespace std;
//将n个在A柱子上的盘子，借助B柱子过渡，最终移动到C柱子上
//A、B、C是柱子编号(char类型) 
void hanoi(int n,char A,char B,char C){
	if(n==0) return;
	//①.将A柱子上最上面的n-1个盘子，借助C柱子过渡，最终移动到B柱子上 
	hanoi(n-1,A,C,B);
	//②.将最下面的第n个盘子从A柱子移动到C柱子上 
	cout<<"第["<<n<<"]个盘子从["<<A<<"]移动到["<<C<<"]"<<endl;
	//③.将第①步移动到B柱子上的n-1个盘子，借助A柱子过渡，最终移动到C柱子上
	hanoi(n-1,B,A,C); 
}
int main()
{
	//8个在'a'柱子上的盘子，借助'b'柱子过渡，最终移动到'c'柱子上 
	hanoi(8,'a','b','c');
	return 0;
}