如果能够将一个大的任务分解成若干个规模较小的任务,而且这些任务的形式与结构与原问题一致,这个时候就可以考虑使用递归。当问题规模足够小或者达到了边界条件就停止递归(需要在递归函数中设计递归出口)。根据前面对递归函数的认识,利用递归分解完问题后还需要对这些规模小的任务合并并返回解,在递归返回的过程中逐级上报,最终解决原问题。
有些问题使用递推和递归都能解决,但是有些问题只能将大问题划分为小问题,不容易建立起递推关系,在这种情况下可以考虑使用递归策略。
一、约瑟夫问题
\(n\) 个人围成一个圆圈,每个人的编号依次是 1、2、3、……、\(n\)。从第一个人开始数数,数到 \(m\) 的人出圈。然后由出圈的下一个人重新数数,数到 \(m\) 的人又出圈……输入 \(n\) 和 \(m\)(\(1 \le n \le 100,1 \le m \le 1,000,000\)),输出最后出圈人的编号。这里只需要输出最后出圈人的编号,如果还用前面介绍的那些求解该问题的方法(在输出依次出圈人的编号的基础上修改为只输出最后出圈人的编号),效率不高。其实本问题还可以用递归的思路求解。
第一轮编号为 \(m\) 的人出圈后,考虑到接下来要继续下一轮,可以对圈内剩下的 \(n-1\) 个人重新编号如下:
| 第一轮开始前的编号 | 1 | 2 | ... | m-2 | m-1 | m | m+1 | m+2 | ... | n-1 | n |
| 第二轮开始前重新编号 | n-m+1 | n-m+2 | n-2 | n-1 | × | 1 | 2 | ... | n-m-1 | n-m |
这样下一轮就变为与原问题本质相同的问题。如果设计一个函数 \(f(n,m)\) 来求解最后出圈那个人的编号,可知此时问题转换为重新编号后 \(f(n-1,m)\) 的结果。对于第一轮编号为 \(x\) 的人,假设下一轮其编号变为 \(y\),由上面的表格分析可知:\(x = (y+m-1)\%n+1\)。这样的推论对于后续轮次同样适用。那么最后出圈那个人的编号 \(f(n,m)\) 就相当于这个公式中的 \(x\),重新编号后 \(f(n-1,m)\) 的结果就相当于这个公式中的 \(y\)。由此可以得出递推公式:\(f(n,m)=(f(n-1,m)+m-1)\%n+1\),递推出口:\(f(1,m)=1\)。下面给出递归和递推的两种解法:
#include<iostream>
using namespace std;
int josephus(int n,int m){
if(n==1) return n;
return (josephus(n-1,m)+m-1)%n + 1;
}
int main(){
int n,m;
cin>>n>>m;
cout<<josephus(n,m)<<endl;
return 0;
}
#include<iostream>
using namespace std;
int main(){
int n,m;
cin>>n>>m;
int ans = 1;
for(int i=2;i<=n;i++){
ans = (ans+m-1)%i + 1;
}
cout<<ans<<endl;
return 0;
}
二、P1028 数的计算
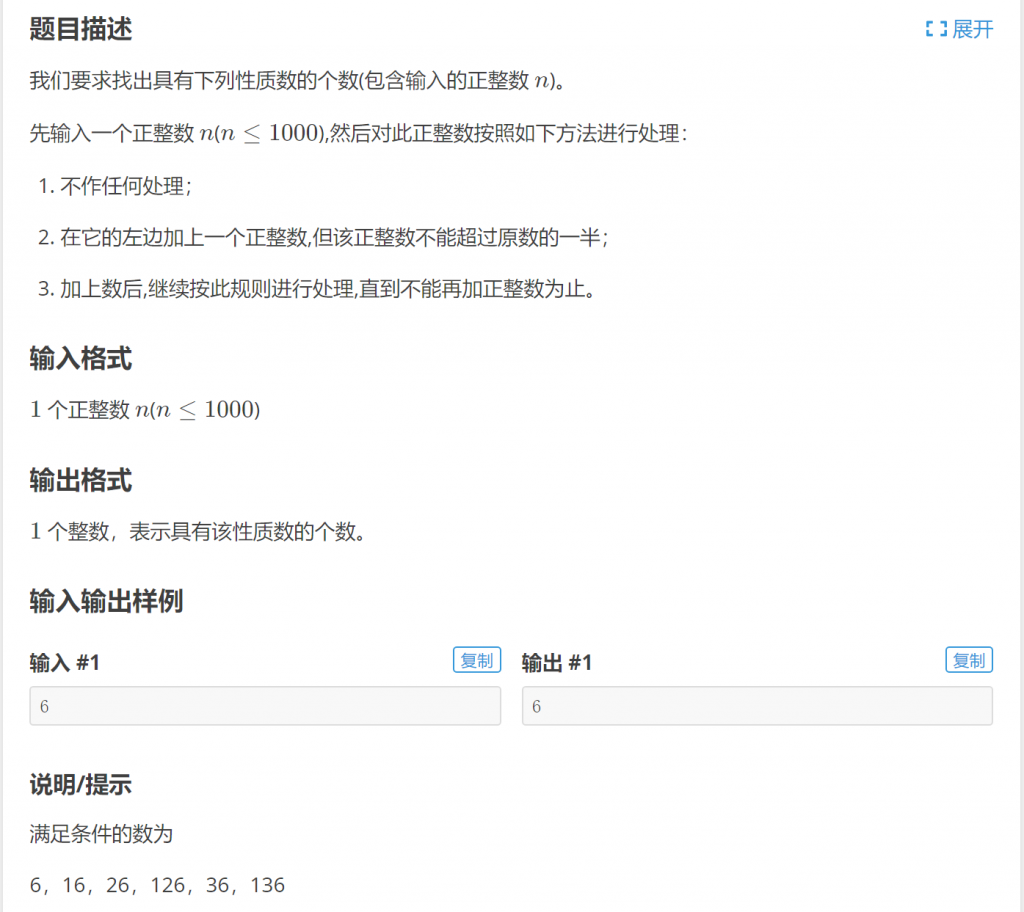
分析:从问题的描述就能看出是一个典型的递归问题。这里设计一个函数 int solve(int n); 用来计算对整数 \(n\) 按照题目描述的规则的生成的数的个数。除了整数 \(n\) 自身外,在整数\(n\) 的左边添加上一个整数 \(i(1 \le i \le \frac{n}{2})\),能够得到一个新的整数 \(\overline{in}\),然后继续对 \(i\) 执行类似处理,继续在左边添加数字。可知对整数 \(n\) 和对整数 \(i\) 的处理过程没有本质区别,对整数 \(i\) 的处理可以递归调用 solve(i)。并且对 \(i\) 的每一种处理最终得到的数其实都对应了一种对整数 \(n\) 的处理最终得到的数,这里应该使用累加结构将所有 \(i\) 的处理结果累加作为 \(n\) 的处理结果:
#include<iostream>
using namespace std;
int solve(int n){
if(n==1) return 1; //递归出口,整数1处理后只有1个数(1)
int ans = 1; //ans记录按规则产生数的数量,考虑n自身,初值为1
//左边添加一个小于n一半的整数i,
//每个i按照同样规则产生的数拼接上n就是n按照规则产生的数
//由上分析可知需要将每个i递归调用处理的结果累加到ans
for(int i=1;i<=n/2;i++)
ans += solve(i);
return ans;
}
int main()
{
int n;
cin>>n;
cout<<solve(n)<<endl;
return 0;
}
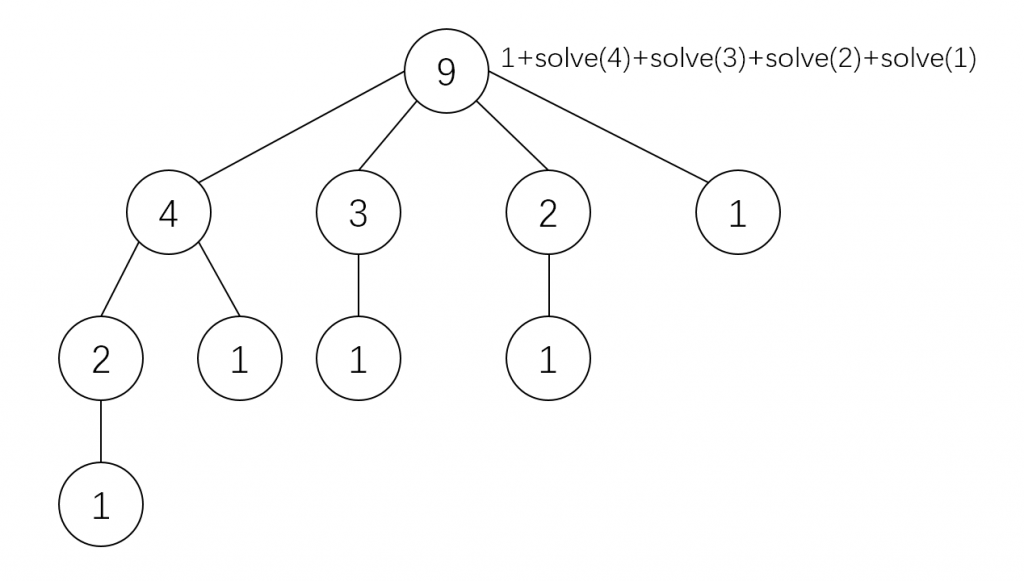
问题的规模是 \(n \le 1000\),输入 1000,会发现不能在 1s 内得出结果。原因是在调用 solve(n) 的过程中,会出现大量重复调用的情况。如上图分析,在调用 solve(9) 的过程中调用 5 次 solve(1)。读者可以修改程序加以验证,在调用 solve(1000) 的过程中,调用次数超过七位数的情况如下:
调用solve(1):990735939次 调用solve(2):394048909次 调用solve(3):202638121次 调用solve(4):117294365次 调用solve(5):74116423次 调用solve(6):50177633次 调用solve(7):35166123次 调用solve(8):25030757次 调用solve(9):18147185次 调用solve(10):13523797次 调用solve(11):10414993次 调用solve(12):8276901次 调用solve(13):6734609次 调用solve(14):5549397次 调用solve(15):4585969次 调用solve(16):3779685次 调用solve(17):3103887次 调用solve(18):2542505次 调用solve(19):2080883次 调用solve(20):1705389次 调用solve(21):1403415次 调用solve(22):1163377次
这么多重复的调用耗费了太多的时间导致超时,可以借助全局数组来避免重复调用情况的发生:
#include<iostream>
using namespace std;
int f[1001];
int solve(int n){
if(f[n]) return f[n];
//n==1的递归出口可以省略(因为n==1时不进后面的循环)
int ans = 1; //ans记录按规则产生数的数量,考虑n自身,初值为1
//左边添加一个小于n一半的整数i,
//每个i按照同样规则产生的数拼接上n就是n按照规则产生的数
//由上分析可知需要将每个i递归调用处理的结果累加到ans
for(int i=1;i<=n/2;i++)
ans += solve(i);
return f[n] = ans;
}
int main()
{
int n;
cin>>n;
cout<<solve(n)<<endl;
return 0;
}
递归函数处理的过程中将计算结果保存到了全局数组中,并且在递归函数的开始处去判断全局数组第 \(n\) 项值(也就是 solve(n) 的结果)的情况,如果不是默认值 0,那么肯定在之前递归调用的过程中已经计算过了(并且保存到了数组中),那么直接返回保存在数组中的结果即可。这样就能有效避免递归调用出现的重复计算。这里的做法称为“记忆化搜索”。在前面递归函数部分介绍 斐波那契数列 也提到了这样的编程思想。
其实这里也可以使用递推的思想来解决问题,和递归的分析思路一致,不难得出递推公式为:
\(f_n=1+f_1+f_2+f_3+...+f_{\frac{n}{2}}\),初始值:\(f_1=1\)
#include<iostream>
using namespace std;
int f[1001];
int main()
{
int n;
cin>>n;
for(int i=1;i<=n;i++){
f[i] = 1;
for(int j=1;j<=i/2;j++){
f[i] += f[j];
}
}
cout<<f[n]<<endl;
return 0;
}
上面的递推算法时间复杂度是 \(O(n^2)\),也出现了重复的计算,可以进一步改进。定义一个数组 s,s[n] = f[1]+f[2]+f[3]+...+f[n](这里用到了前缀累加和的思想),那么可知 f[n] = 1+s[n/2],s[n] = s[n-1]+f[n],这样可以将算法时间复杂度降低到 \(O(n)\):
#include<iostream>
using namespace std;
int f[1001],s[1001];
int main()
{
int n;
cin>>n;
for(int i=1;i<=n;i++){
f[i] = 1 + s[i/2];
s[i] = s[i-1]+f[i];
}
cout<<f[n]<<endl;
return 0;
}
其实递推公式还可以描述为:
\(\begin{equation} f_n=\left\{ \begin{aligned} f_{n-1}\quad(n\%2==1) \\ f_{n-1}+f_{n/2}\quad(n\%2==0)\end{aligned} \right. \end{equation}\),初始值:\( f_1=1\)
#include<iostream>
using namespace std;
int f[1001];
int main()
{
int n;
cin>>n;
f[1] = 1;
for(int i=2;i<=n;i++){
f[i] = f[i-1];
if(i%2==0) f[i] += f[i/2];
}
cout<<f[n]<<endl;
return 0;
}
一般情况下,如果能够使用递推算法替换递归算法,程序执行的效率会提高(递归函数调用以及返回过程中需要耗费一些时间)。但是这个例子使用记忆化搜索优化后的递归策略执行效率会高于递推策略。递推需要从 1~n 一步一步推导才能得到结果 f[n],而调用递归函数 solve(n),只需要计算 solve(1)~solve(n/2)。
三、P1464 Function

分析:使用多个参数的递归函数求解问题,借助记忆化搜索的策略来避免递归函数中出现重复的计算:
#include<iostream>
using namespace std;
typedef long long LL; //为long long类型起了一个别名LL
LL ans[21][21][21];
LL w(LL a,LL b,LL c){
if(a<=0||b<=0||c<=0) return 1;
else if(a>20||b>20||c>20) return w(20,20,20);
else if(ans[a][b][c]) return ans[a][b][c];
else if(a<b&&b<c)
return ans[a][b][c]=w(a,b,c-1)+w(a,b-1,c-1)-w(a,b-1,c);
else
return ans[a][b][c]=w(a-1,b,c)+w(a-1,b-1,c)+w(a-1,b,c-1)-w(a-1,b-1,c-1);
}
int main()
{
LL a,b,c;
cin>>a>>b>>c;
while(a!=-1 || b!=-1 || c!=-1){
cout<<"w("<<a<<", "<<b<<", "<<c<<") = ";
cout<<w(a,b,c)<<endl;
cin>>a>>b>>c;
}
return 0;
}
四、P1928 外星密码
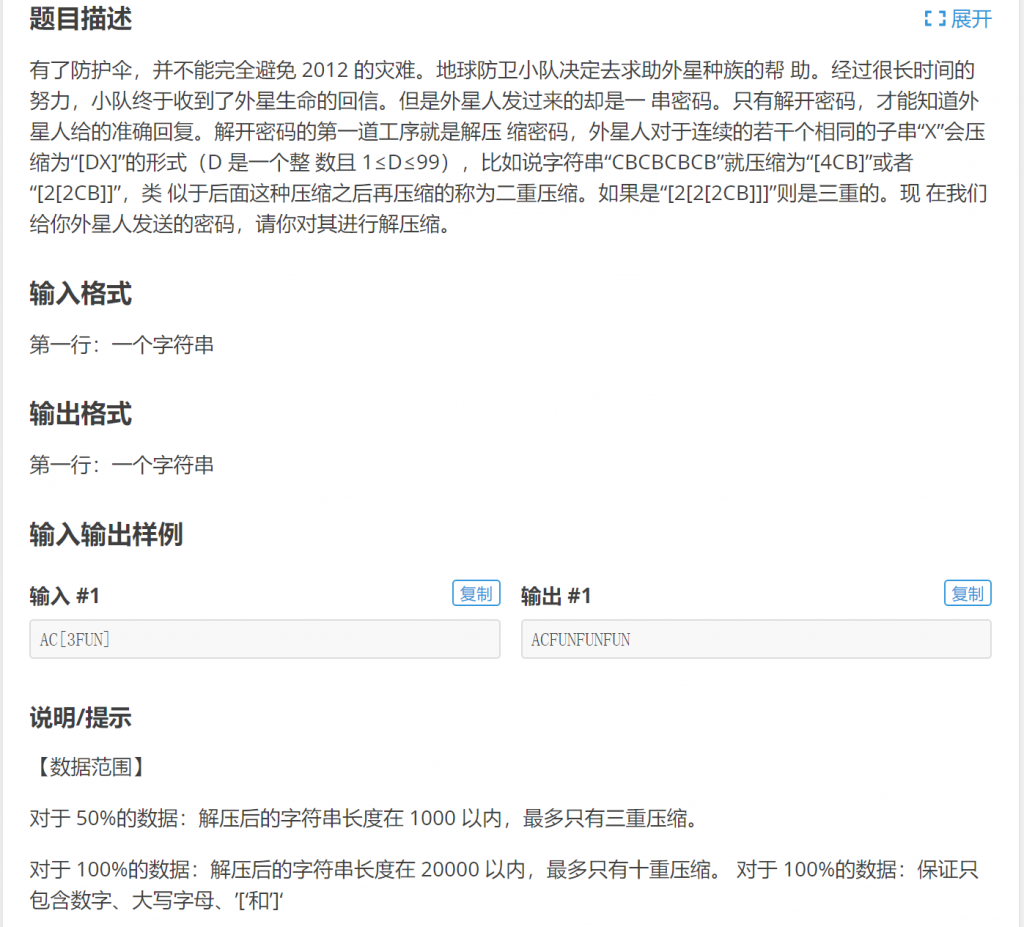
分析:如果只有一层 [],那么很好处理,依次读入字符找到 '[' 后就能立即读入重复次数,再继续读入重复次数后面的字符,然后按照重复次数还原即可。如果有多层 [],那么读到重复次数后,再读取的可能是压缩区域,可知这些压缩区域的处理方式和外层的处理方式是相同的,可以将整个处理过程设计成递归函数:
#include<iostream>
#include<string>
using namespace std;
string expand(){
string ans,tmp;
char ch;
int count;
//一直读取字符,直到读到']'(被递归调用时)或者全部读完为止(main调用时)
while(cin>>ch){
if(ch=='['){ //读到'[',进入压缩区域
cin>>count; //读取压缩次数
tmp = expand(); //递归调用,一直会读到与本次'['配对的']'为止
//tmp重复count次,拼接到ans后
while(count--) ans += tmp;
}else if(ch==']'){ //读到']',return结果(被递归调用时才会读到)
return ans;
}else{ //其它字符,直接拼接到ans后
ans += ch;
}
}
//只有main函数调用expand才会执行到这里,递归调用不能
return ans;
}
int main()
{
cout<<expand()<<endl;
return 0;
}
上面的程序理解起来还是有一定的难度,读者可以结合注释内容自行举例分析执行过程,帮助理解。可以试试这些样例:a[3bc]de、abf[4ra[2a]bc[3e]]。
五、P1010 幂次方

分析:可以先考虑将整数 \(n\) 用 2 的幂次方表示的问题。其实这是一个将十进制数 \(n\) 转换成二进制数的问题。回顾前面介绍的进制转换:
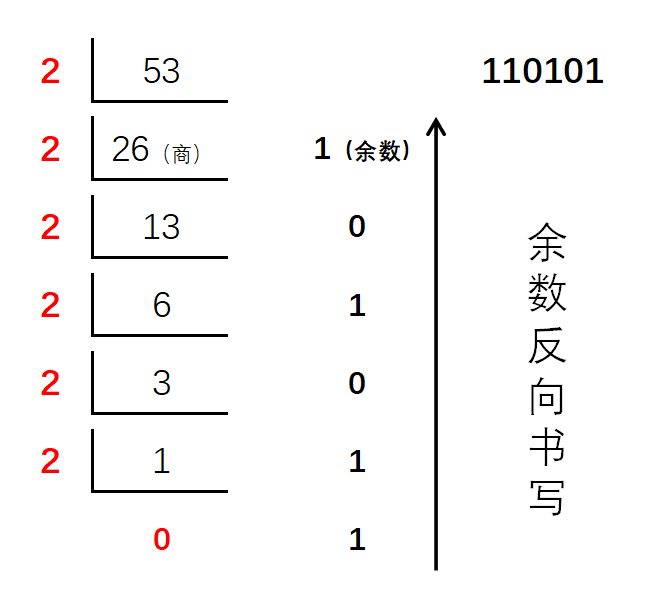
上面的转换二进制的过程可以用递归实现:
#include<iostream>
using namespace std;
//十进制n转二进制
void work(int n){
if(n==0) return;
work(n/2); //递归调用:同样的方法处理n/2
cout<<n%2; //先递归调用再输出余数,保证最终输出效果是所有余数逆序
}
int main(){
for(int i=1;i<=1024;i++){
cout<<i<<":";
work(i);
cout<<endl;
}
return 0;
}
实现了十进制转二进制,那么就可以想办法将整数 \(n\) 用 2 的幂次方表示。其实上面递归函数中如果 n%2!=0,那么就对应了用 2 的幂次方表示的一项,但是还要想办法记录下来这一项究竟是 2 的多少次方。考虑到递归处理过程中,每递归调用一次,次方数其实就要 +1,那么可以设计一个两个参数的递归函数来实现将整数 \(n\) 用 2 的幂次方表示:
#include<iostream>
using namespace std;
//十进制n用2的幂次方表示
void work(int n,int k){
if(n==0) return;
work(n/2,k+1); //递归调用:同样的方法处理n/2
if(n%2){
if(n/2) cout<<"+"; //输出的第1项前面没有+
cout<<2<<"("<<k<<")"; //cout<<2<<"^"<<k;
}
}
int main(){
for(int i=1;i<=1024;i++){
cout<<i<<":";
work(i,0);
cout<<endl;
}
return 0;
}
在此基础上,就能继续改进递归函数内容实现原题要求的效果。输出的每一项如果幂为 0 或者为 1,可以直接按要求格式输出,如果幂大于等于 2,那么幂也要按照规则转换成用 2 的幂表示的形式,需要继续递归调用:
#include<iostream>
using namespace std;
void work(int n,int k){
if(n == 0) return;
work(n/2,k+1);
if(n%2){
if(n/2) cout<<"+"; //第1项前不能有+
//k是次方,k==0和k==1按照题目格式直接输出
//k>=2时需要递归继续处理k表示成2的幂次方的形式
if(k == 0){
cout<<"2(0)";
}else if(k == 1){
cout<<"2";
}else{
cout<<"2(";
work(k,0);
cout<<")";
}
}
}
int main(){
int n;
while(cin>>n){
work(n,0);
cout<<endl;
}
return 0;
}
这个问题其实还可以通过打表的策略求解:
#include<iostream>
#include<string>
using namespace std;
/***************************************************************/
//在表(数组)中记录作为幂的整数的“表示为2的幂次方的形式”
//考虑数据规模,只需要记录下0~16即可
/***************************************************************/
string Table[] = {
"(0)", //\(2^0\)表示为2(0),幂0的表示形式为"(0)"
"", //\(2^1\)表示为2,幂1的表示形式为""
"(2)", //\(2^2\)表示为2(2),幂2的表示形式为"(2)"
"(2+2(0))", //\(2^3\)表示为2(2+2(0)),幂3的表示形式为"(2+2(0))"
"(2(2))",
"(2(2)+2(0))",
"(2(2)+2)",
"(2(2)+2+2(0))",
"(2(2+2(0)))",
"(2(2+2(0))+2(0))",
"(2(2+2(0))+2)",
"(2(2+2(0))+2+2(0))",
"(2(2+2(0))+2(2))",
"(2(2+2(0))+2(2)+2(0))",
"(2(2+2(0))+2(2)+2)",
"(2(2+2(0))+2(2)+2+2(0))",
"(2(2(2)))"
};
/***************************************************************/
int ans[20];
int main(){
int n;
while(cin>>n){
//分解出n表示为2的幂次方的所有幂,存储到数组中
int k = 0,tot = 0;
while(n){
if(n%2) ans[++tot] = k; //余数不为0,有k次幂,记录到数组
n /= 2; k++;
}
//存储在数组中的每一项幂通过查表找出幂的“表示为2的幂次方的形式”的表示方法
for(int i=tot;i>=1;i--){
cout<<"2";
cout<<Table[ans[i]];
if(i!=1) cout<<"+";
}
}
return 0;
}
 NOIP学习小站
NOIP学习小站