NOIP学习小站搜索与回溯是计算机解题中常用的算法。搜索的策略是先选择一个起点开始向前探索，逐渐扩大寻找范围，在探索过程中一旦发现之前的选择是错误的，就退回一步重新选择（回溯），继续向前探索，如此反复进行，直到得到解或者证明问题无解。回溯是搜索算法的一种控制策略。其实搜索也是暴力枚举的一种有效策略。
一、搜索与回溯
以走迷宫为例，一个 \(N \times M\) 的迷宫，指定了入口和出口坐标，并给出了迷宫中的所有墙壁（障碍点）的坐标，要计算从入口走到出口的方案数。因为在一个点可能有 4 个方向可以走，这里设定在一个点的试探方向依次为：向下\(→\)向右\(→\)向上\(→\)向左。进入迷宫后，选择方向向下，一步步向前试探前进，如果当前方向上遇到墙壁，可以在当前点（可能沿着预定方向已经走了很多步了）看看有没有其它方向可走，如果有那么就沿着新方向继续前进试探；如果四个方向都无路可走，说明碰到死胡同，那么回退到前一点，再看看其它方向是否还有路可走，如果有路可走，则沿着该方向继续前进试探。上面描述的过程中：向前试探就是搜索，发现无路可走回退就是回溯。
首先结合例图来分析没有回溯过程的搜索过程，图中灰色块表示墙壁。注意设定了搜索方向次序为：向下\(→\)向右\(→\)向上\(→\)向左，搜索具体过程如下：
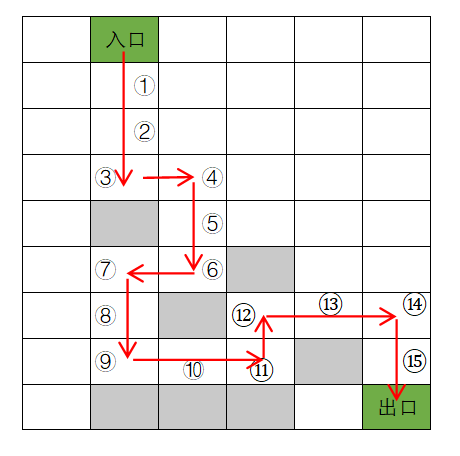
- 从入口一直向下搜索，途径①②③；
- 在③处无法继续向下搜索（碰到墙壁），按照设定的搜索方向次序，向右搜索，来到④；
- 在④处按照搜索方向次序，向下搜索（而不是继续向右搜索），途经⑤⑥；
- 在⑥处无法继续向下搜索（碰到墙壁），也不能向右（碰到墙壁），也不能向上（不能走之前走过的点），只能向左，来到⑦；
- 在⑦处按照搜索方向次序，向下搜索（而不是继续向左搜索），途经⑧⑨；
- 在⑨处无法继续向下搜索（碰到墙壁），向右搜索来到⑩；⑩处和⑨处类似，向右搜索来到⑪；
- 在⑪处无法向下、向右搜索（碰到墙壁），向上搜索来到⑫；
- 在⑫处不能向下搜索（不能走之前走过的点），向右搜索来到⑬；
- 在⑬处不能向下搜索（碰到墙壁），向右搜索来到⑭；
- 在⑭处一直向下搜索途经⑮，最后来到出口。
再来看有回溯过程的情况，如下图所示，搜索具体过程如下：
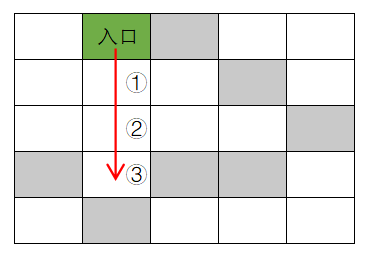
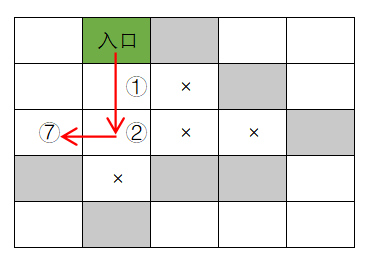
- 从入口一直向下搜索，途径①②③；
- 在③处，向下、向右搜索都不行（碰到墙壁），不能向上搜索（不能走之前走过的点），也不能向左搜索（碰到墙壁），走进了死胡同，那么只能回退一步，重新回到②，考虑②处的下一个搜索方向（向右，②处上一次搜索方向是向下）；
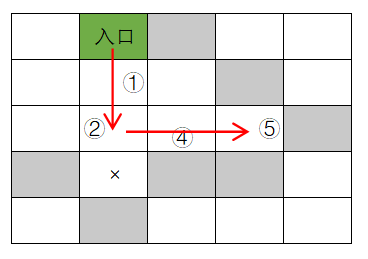
- 在②处，向右搜索来到④；
- 在④处，不能向下搜索（碰到墙壁），向右搜索来到⑤；
- 在⑤处，向下、向右、向上搜索都不行（碰到墙壁），也不能向左搜索（不能走之前走过的点），走进了死胡同，那么只能回退一步，重新回到④，考虑④处的下一个搜索方向（向上，④处上一次搜索方向是向右）；
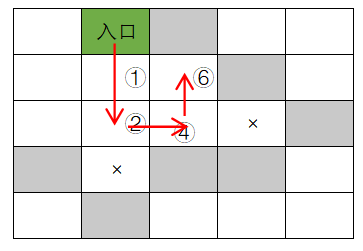
- 在④处，向上搜索来到⑥；
- 在⑥处，不能向下搜索（不能走之前走过的点），也不能向右、向上搜索（碰到墙壁），不能向左搜索（不能走之前走过的点），⑥处四个方向都探索了，都不行，只能回退一步，重新回到④，考虑④处的下一个搜索方向（向左，④处上一次搜索方向是向上）；
- 在④处，不能向左搜索（不能走之前走过的点），④处四个方向都探索了，都不行。那么只能回退一步，重新回到②，考虑②处的下一个搜索方向（向上，②处上一次搜索方向是向右）；
- 在②处，不能向上搜索（不能走之前走过的点），向左搜索，来到⑦；
- 继续搜索（后面过程略）。
如果将迷宫中的点编序号，搜索过程可以用下面的解答树表示：
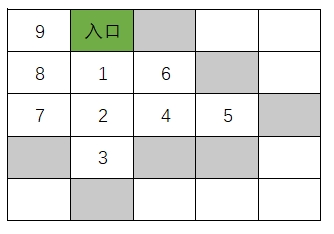
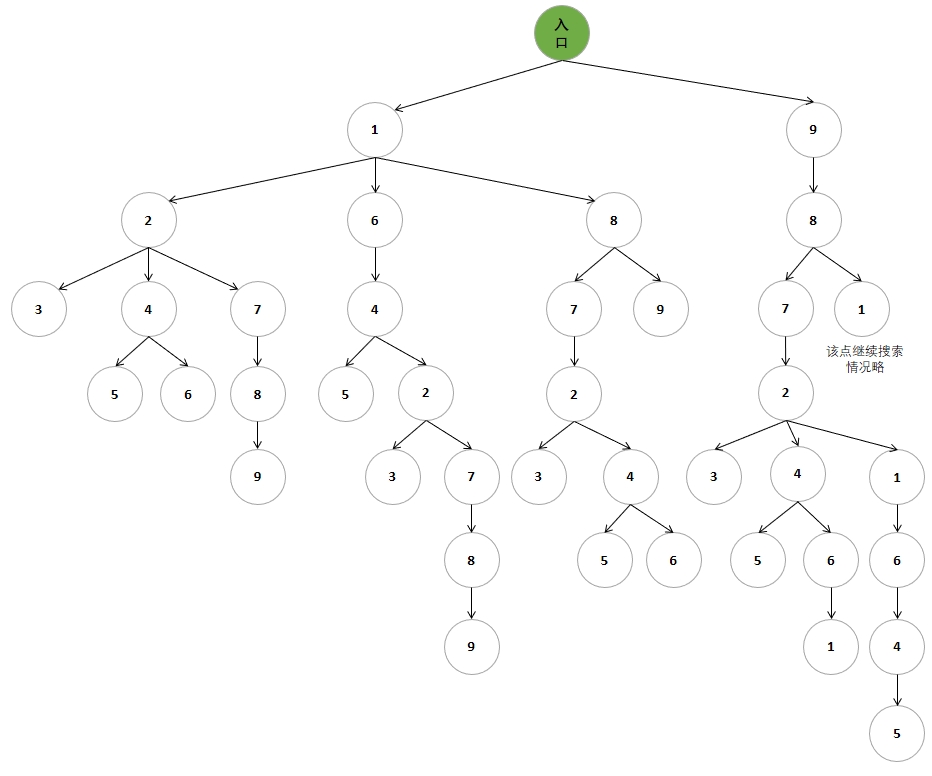
结合解答树，可知解答树上每个点都要进行四个方向的试探，这里可以借助循环枚举四个方向。如果从 A 点能走到 B 点，可知 B 点继续试探的处理策略和 A 完全一致。如果用函数 dfs 来实现 A 点的处理，可知在 dfs 函数内部要有走到 B 点后的继续处理过程，而这个继续处理过程仍然可以调用 dfs 函数来实现，这里是很明显的递归调用过程。
二、深度优先搜索算法（DFS）
搜索与回溯算法常用深度优先搜索算法（DFS，Depth-first search）来实现，深度优先搜索算法往往借助递归函数来实现，并且有基本的框架：
void dfs(int k){
if(到达目的地){
输出解;
return;
}
for(枚举下一步的每一种情况){
if(满足条件){
保存结果;
dfs(k+1);
恢复到保存结果之前的状态（回溯一步）
}
}
} void dfs(int k){
for(枚举下一步的每一种情况){
if(满足条件){
保存结果;
if(到达目的地) 输出解;
else dfs(k+1);
恢复到保存结果之前的状态（回溯一步）
}
}
} 来分析递归函数 void dfs(int k) 的一些细节：
- 开始部分如果发现搜索已经到达目的地，那么直接输出解并return，这一部分其实是递归函数的出口；
- 通过循环来枚举搜索过程中下一步的所有情况，例如上面走迷宫的四个方向对应的下一个点；
- 对于枚举的每一种情况，要判断是否满足条件，例如上面走迷宫的四个方向中对应的点中有一个是上一步从该点走过来的，或者有可能是前面若干步走过的，不能走之前走过的点，不满足条件；或者某个方向上的点是墙壁，那也不满足条件；
- 满足条件时需要保存结果，例如要输出走迷宫的具体方案，需要想办法将这一步的坐标点记录到全局数组中；并且还要记录下当前这一点已经走过了（可以使用全局数组来标记），这样在后面搜索的过程中才能在条件判断时保证不走之前走过的点；
- 循环中递归调用
dfs(k+1);，对于每一种满足条件的情况，继续按照相同的策略搜索下一步的情况； - 递归调用后需要回溯，这一点初学者容易忘记。回溯主要的代码是“恢复到保存结果之前的状态”。例如走迷宫搜索过程中，在递归调用之前要标记当前点已经走过了，在递归调用后回溯时需要将该点的标记状态恢复成没有走过。
搜索的过程中产生方案，每一种方案是由很多步组成的，递归函数void dfs(int k)的参数 k 就指明了方案上每一步的编号。
上面走迷宫问题有点复杂，这里先来看一个简单的问题：按照字典顺序输出 1～\(n\) 这 \(n\) 个整数的全排列。
三、全排列
前面学习暴力枚举策略已经介绍过全排列问题，这里使用深度优先搜索来解决。1～\(n\) 这 \(n\) 个整数全排列，可以依次考虑第 1、2、3、...、\(n\) 个位置用 1～\(n\) 哪一个数字。
1.全排列结果中数字可以重复
如果排列结果中数字可以重复，那么每一个位置都可以使用 1～\(n\) 的任意一个数字，使用上面的DFS框架，dfs(k) 就是考查第 \(k\) 个位置用哪一个数字，函数体中递归调用 dfs(k+1) 就是在第 \(k\) 个位置用了某个数的基础上继续搜索考查第 \(k+1\) 这个位置用哪一个数字。套用DFS框架，参考程序如下：
#include<iostream>
using namespace std;
const int MAX = 20;
//n定义成全局变量
int n;
//ans用来记录全排列的一种方案
int ans[MAX+1];
//搜索第k个位置用哪一个数
void dfs(int k){
if(k==n+1){ //现在考虑到了第n+1个位置用哪个数字，已经到达“目的地”（递归出口）
//输出搜索出来的一个全排列方案（方案保存在ans数组中）
for(int i=1;i<=n;i++) cout<<ans[i]<<" ";
cout<<endl;
return;
}
//第k个位置可以用1～n的任意一个数i
for(int i=1;i<=n;i++){
ans[k] = i; //第k个位置用i，记录到ans数组中
dfs(k+1); //在第k个位置用i的基础上，继续搜索第k+1这个位置用哪一个数字
}
}
int main(){
cin>>n;
//主函数只需要调用dfs(1)，以“考虑第1个位置用哪一个数”为搜索起点
dfs(1);
return 0;
} 
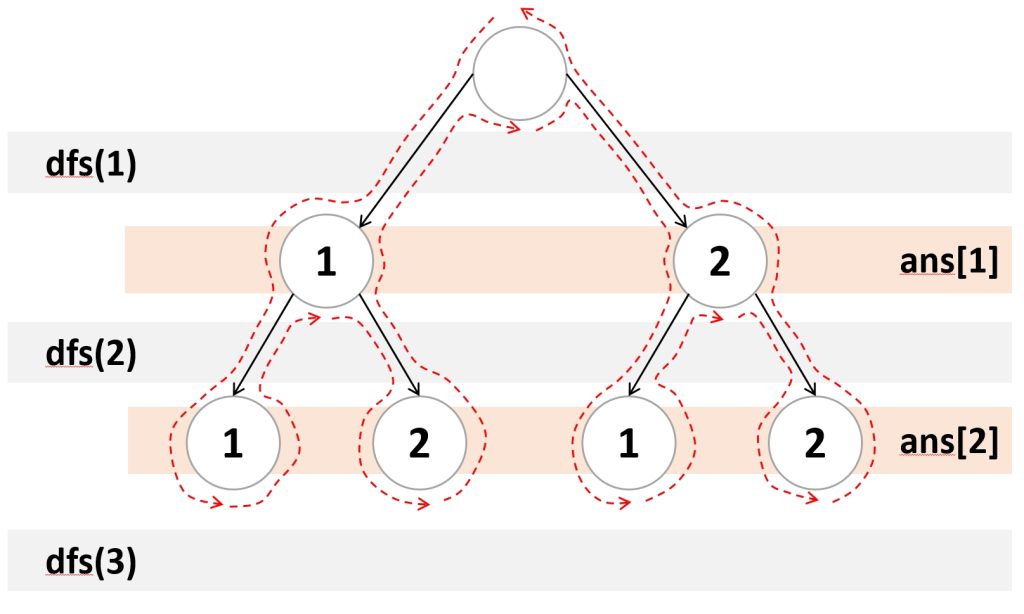
仔细体会上面DFS的作用，每个位置上数都可以用 1～\(n\) 的任意一个数，而在确定了当前位置（\(k\)）处的数的基础上借助递归调用去搜索下一个位置（\(k+1\)）用哪一个数。有点类似于实现了一个“\(n\) 重循环的效果”，而“循环层级 \(n\) ”是动态的！
2.全排列结果中数字不可以重复
如果排列中数字不可以重复，那么第 1 个位置可以用 1～\(n\) 的任意一个数字，第 2 个位置可以用 1～\(n\) 的任意一个前面没有使用的数字，第 3 个位置可以用 1～\(n\) 的任意一个前面没有使用的数字，...，第 \(n\) 个位置依然如此（虽然此时只剩下一个数字可以用）。
使用上面的DFS框架，dfs(k) 仍然是考查第 \(k\) 个位置用哪一个数字，函数体中递归调用 dfs(k+1)就是在第 \(k\) 个位置用了某个符合条件的数的基础上继续搜索考查第 \(k+1\) 个位置用哪一个数字，这里要通过条件判断确保排列中不出现重复的数字。套用DFS框架，参考程序如下：
#include<iostream>
using namespace std;
const int MAX = 20;
//n定义成全局变量
int n;
//ans用来记录全排列的一种方案
int ans[MAX+1];
//used[i]用来记录在搜索过程中整数i是否被使用过
int used[MAX+1];
//搜索第k个位置用哪一个数
void dfs(int k){
if(k==n+1){ //现在考虑到了第n+1个位置用哪个数字，已经到达“目的地”（递归出口）
//输出搜索出来的一个全排列方案（保存在ans数组中的）
for(int i=1;i<=n;i++)
cout<<ans[i]<<" ";
cout<<endl;
return;
}
//第k个位置粗略来看，可以用1～n的任意一个数i
for(int i=1;i<=n;i++){
//还有一个前提，就是在前面确定第1、第2...第k-1个位置的数时候没有用过i
if(!used[i]){
ans[k] = i; //第k个位置用i，记录到ans数组中
used[i] = 1; //标识搜索过程中数字i被使用了
dfs(k+1); //在第k个位置用i的基础上，继续搜索第k+1个位置用哪一个数字
used[i] = 0; //回溯，重新标识数字i没有被使用
}
}
}
int main(){
cin>>n;
//主函数只需要调用dfs(1)，以“考虑第1个位置用哪一个数”为搜索起点
dfs(1);
return 0;
} 运行程序，输入3，程序运行时各函数详细调用与返回过程（部分）如下：
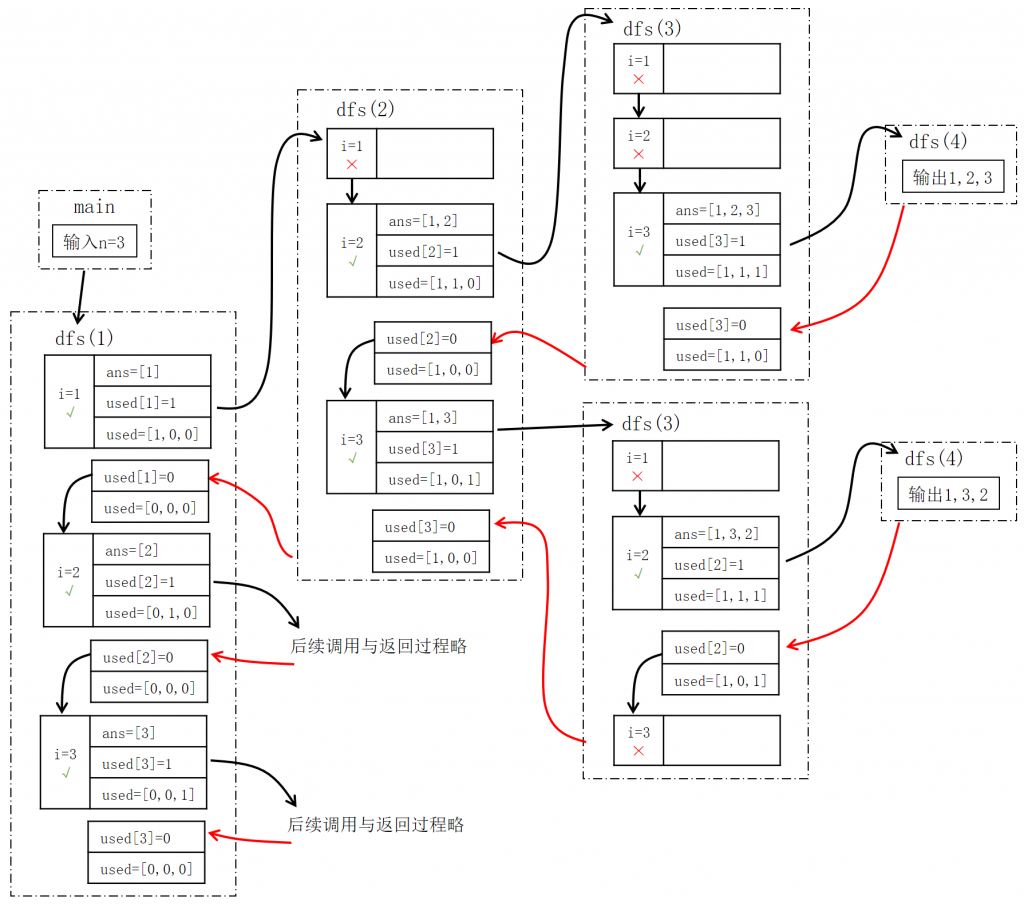
运行过程还可以通过下面这个图来分析：
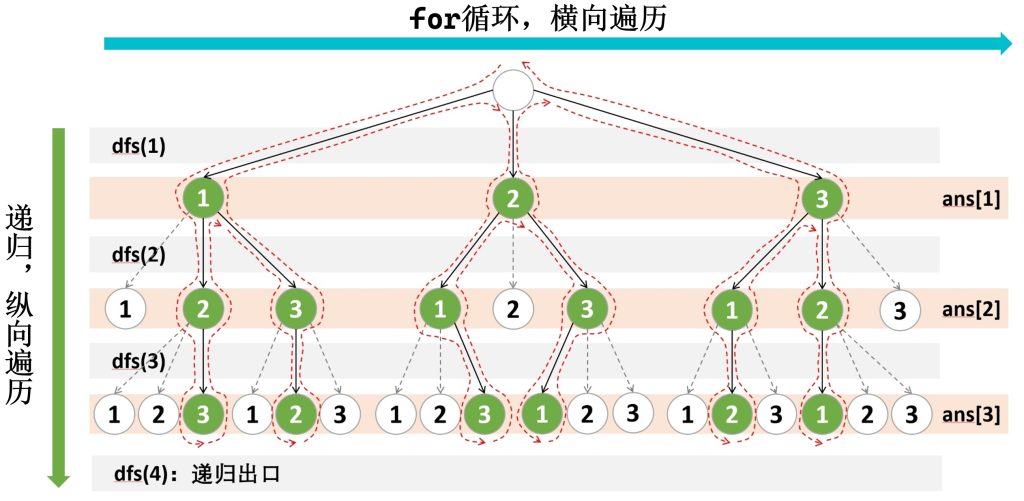
如果考虑回溯的过程，运行情况如下图所示（没有画出不符合条件的情况）：
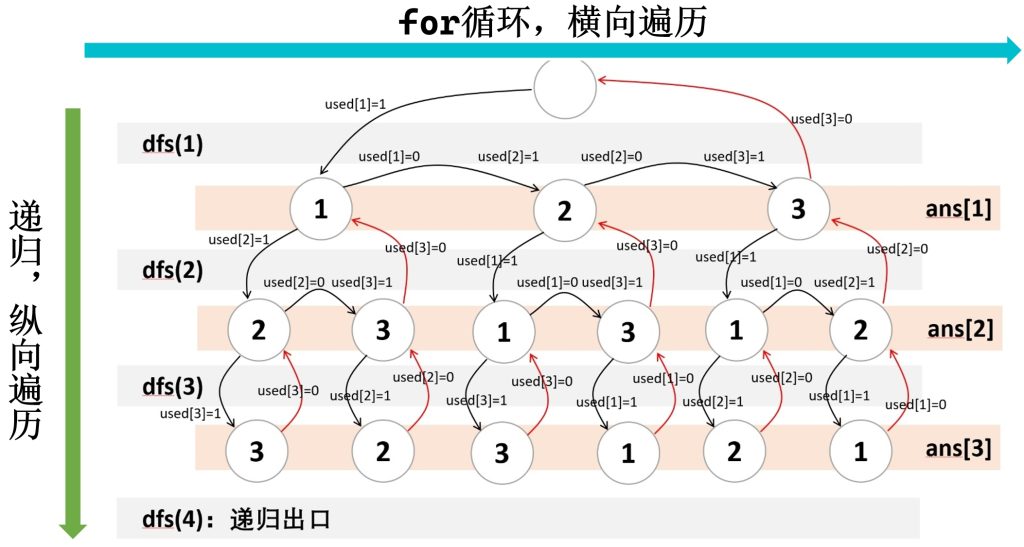
从上图可知，正因为在回溯过程中将数字的使用状态恢复为未使用，在后面的搜索过程中才能继续使用这些数字！初学者容易遗忘这一点，需要特别注意！
3.搜索每个数存放的位置
还可以搜索每个数存放的位置来生成全排列。下面的程序用存储在数组 a 的 a[1]～a[n] 中的 \(n\) 个数（不存在相同的数）通过搜索每个数存放的位置来生成全排列：
#include<iostream>
using namespace std;
const int MAX = 20;
//has数组用来标记全排列的每个位置是否已经放好了数
int a[MAX+1],ans[MAX+1],has[MAX+1],n,cnt = 0;
//搜索第k个数放的位置
void dfs(int k){
if(k==n+1){ //现在考虑到了第n+1个数放在哪个位置，已经到达“目的地”（递归出口）
cnt++;
//输出搜索出来的一个全排列方案（保存在ans数组中的）
for(int i=1;i<=n;i++){
cout<<ans[i]<<" ";
}
cout<<endl;
return;
}
//粗略来看，第k个数可以放在1～n的任意位置
for(int i=1;i<=n;i++){
if(!has[i]){ //第i个位置没有数才能放
ans[i] = a[k]; //第k个数a[k]放到全排列的第i位，记录到ans数组中
has[i] = 1; //标识搜索过程中第i个位置已经放了数
dfs(k+1); //第k个数放在全排列第i个位置的基础上，继续搜索第k+1个数放的位置
has[i] = 0; //回溯，重新标识第i个位置没有放数
}
}
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
//搜索第1个数放的位置
dfs(1);
cout<<cnt<<endl;
return 0;
}4.全排列去重
如果要全排列的 \(n\) 个数中存在相同的数，可知上面的两种方法搜索策略都会出现重复的全排列情况。可以将“搜索每个数存放的位置来生成全排列”这一方法改进一下：先将 \(n\) 个数排序，搜索第 \(k\) 个数放置位置时如果发现 a[k]==a[k-1]，那么第 \(k\) 个数只能放到第 \(k-1\) 个数的后面。这样就能保证搜索出来的全排列不重复：
//当要全排列的数中有相同的数，本程序能够保证搜索出来的全排列不重复
#include<iostream>
#include<algorithm>
using namespace std;
const int MAX = 20;
//has数组用来标记全排列的每个位置是否已经放好了数
int a[MAX+1],ans[MAX+1],has[MAX+1],n,cnt = 0;
//从位置start开始搜索第k个数放的位置
void dfs(int k,int start){
if(k==n+1){ //现在考虑到了第n+1个数放在哪个位置，已经到达“目的地”（递归出口）
cnt++;
//输出搜索出来的一个全排列方案（保存在ans数组中的）
for(int i=1;i<=n;i++){
cout<<ans[i]<<" ";
}
cout<<endl;
return;
}
//从位置start开始枚举第k个数放的位置
//如果是第1个数或者是和上一个搜索的数不同，那么应该从位置1开始枚举，将start = 1
if(k==1 || a[k] != a[k-1]) start = 1;
//如果第k个数和上一个搜索的数相同，那么从位置start（也就是上一个数存放位置的下个位置）开始枚举
//这样就能保证搜索出来没有重复
for(int i=start;i<=n;i++){
if(!has[i]){ //第i个位置没有数才能放
ans[i] = a[k]; //第k个数a[k]放到全排列的第i位，记录到ans数组中
has[i] = 1; //标识搜索过程中第i个位置已经放了数
//第k个数放在第i个位置的基础上，继续搜索第k+1个数放的位置，初步认为第k+1个数只能放在第k个数的后面
dfs(k+1,i+1);
has[i] = 0; //回溯，重新标识第i个位置没有放数
}
}
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
sort(a+1,a+n+1); //搜索前一定要排序
//从位置1开始搜索第1个数放的位置
dfs(1,1);
cout<<cnt<<endl;
return 0;
}5.通过交换实现全排列
还可以使用交换的策略生成全排列。这里让全排列的 \(n\) 个数存储在数组 a 的 a[1]～a[n] 中。从第 \(1\) 个位置到第 \(n\) 个位置依次确定排列每个位置的数。假设全排列的前 \(k-1\) 个数已经确定存放在 a[1]～a[k-1]中，也就是已经生成了 \(k-1\) 个数的排列，接下来要确定第 \(k\) 个位置的数，那么 a[k] 自身放在第 \(k\) 个位置、a[k] 与 a[k+1] 交换（也就是 a[k+1] 放在第 \(k\) 个位置）、a[k] 与 a[k+2] 交换（也就是 a[k+2] 放在第 \(k\) 个位置）、……、a[k] 与 a[n] 交换（也就是 a[n] 放在第 \(k\) 个位置），这些做法都可以生成一种 \(k\) 个数的排列，在此继续上搜索第 \(k+1\) 个位置的数，又能生成 \(k+1\) 个数的排列……。按照这样的做法可以从第 \(1\) 个位置到第 \(n\) 个位置通过搜索依次确定排列每个位置的数。需要特别注意的是，如果要全排列的 \(n\) 个数中有相同的数，那么 a[k] 与 a[i]（i=k,k+1,k+2,...,n）只有当 a[k]~a[i-1] 中不存在与 a[i] 相等的元素时才能交换，这样就能保证找出的全排列不会出现重复的情况：
//当要全排列的数中有相同的数，本程序能够保证搜索出来的全排列不重复
#include<iostream>
using namespace std;
const int MAX = 20;
int a[MAX+1],n,cnt = 0;
//搜索排列第k个位置上的数
void permutation(int k){
if(k==n+1){
cnt++;
for(int i=1;i<=n;i++){
cout<<a[i]<<" ";
}
cout<<endl;
return;
}
//a[k]与a[i]（i=k,k+1,k+2,...,n）交换
//每种交换都可以确定排列第k个位置上的数
for(int i=k;i<=n;i++){
//排列去重：如果已经在前面枚举过程中出现过与a[i]相同的数就不再处理
bool find = false;
for(int j=k;j<i;j++){
if(a[j]==a[i]){
find = true;
break;
}
}
if(find) continue;
swap(a[k],a[i]);
//搜索排列第k+1个位置上的数
permutation(k+1);
swap(a[k],a[i]);
}
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
//搜索排列第1个位置上的数
permutation(1);
cout<<cnt<<endl;
return 0;
}四、输出组合
前面学习暴力枚举策略时已经介绍过子集枚举可以解决组合问题，这里使用深度优先搜索来解决。从 1～\(n\) 这 \(n\) 个整数选择 \(m\) 个不同的数构成组合，输出所有的组合情况。
1.由排列到组合
前面的全排列是 1～\(n\) 这\(n\) 个数中选 \(n\) 个数排列，这里是 1～\(n\) 这 \(n\) 个数中选 \(m\) 个数组合，在前面全排列的程序代码基础上稍微改动，可以得出一个初步的代码：
//本程序实现的是1～n这n个数中选m个数的所有排列，并不是组合
#include<iostream>
using namespace std;
const int MAX = 20;
//n、m定义成全局变量
int n,m;
//ans用来记录组合的一种方案
int ans[MAX+1];
//used[i]用来记录在搜索过程中整数i是否被使用过
int used[MAX+1];
//搜索第k个数用哪一个数
void dfs(int k){
if(k==m+1){ //现在考虑到了第m+1个数用哪个数字，已经到达“目的地”（递归出口）
//输出搜索出来的一个组合方案（方案保存在ans数组中）
for(int i=1;i<=m;i++) cout<<ans[i]<<" ";
cout<<endl;
return;
}
//第k个数粗略来看，可以用1～n的任意一个数i
for(int i=1;i<=n;i++){
//还有一个前提，就是在前面考虑第1、第2、第k-1个数的时候没有用过i
if(!used[i]){
ans[k] = i; //第k个数用i，记录到ans数组中
used[i] = 1; //标识搜索过程中数字i被使用了
dfs(k+1); //在第k个数用i的基础上，继续搜索第k+1个数用哪一个数字
used[i] = 0; //回溯，重新标识数字i没有被使用
}
}
}
int main(){
cin>>n>>m;
//主函数只需要调用dfs(1)，以“考虑第1个数用哪一个数”为搜索起点
dfs(1);
return 0;
} 组合内的元素是不讲顺序的（例如组合[1,2,3]和[1,3,2]、[2,3,1]都是同一个组合），而上面的程序实现的是 1～\(n\) 这 \(n\) 个数中选 \(m\) 个数排列，并不是组合，输出的结果中出现了大量重复组合的情况。
如何真正实现组合呢？其实只需要新添加一个规则，那就是第 \(k+1\) 个数必须比第 \(k\) 个数大，也就是后面使用的数要大于前面使用的数。有了这个规则后，在搜索的过程中都不用再设计数组来记录数字有没有被使用过，因为后面的数大于前面的数，肯定不会重复使用：
#include<iostream>
using namespace std;
const int MAX = 20;
//n、m定义成全局变量
int n,m;
//ans用来记录组合的一种方案
int ans[MAX+1];
//搜索第k个数用哪一个数
void dfs(int k){
if(k==m+1){ //现在考虑到了第m+1个数用哪个数字，已经到达“目的地”（递归出口）
//输出搜索出来的一个组合方案（方案保存在ans数组中）
for(int i=1;i<=m;i++) cout<<ans[i]<<" ";
cout<<endl;
return;
}
//第k个数可以用ans[k-1]+1～n的任意一个数i
for(int i=ans[k-1]+1;i<=n;i++){ //循环条件可以进一步限制为：m-k+i<=n
ans[k] = i; //第k个数用i，记录到ans数组中
dfs(k+1); //在第k个数用i的基础上，继续搜索第k+1个数用哪一个数字
}
}
int main(){
cin>>n>>m;
//主函数只需要调用dfs(1)，以“考虑第1个数用哪一个数”为搜索起点
dfs(1);
return 0;
} 前面介绍的子集枚举算法输出组合，时间复杂度是 \(O(2^n)\)（由数学知识可知\(2^n=\mathrm{C}_n^0+\mathrm{C}_n^1+\mathrm{C}_n^2+...+\mathrm{C}_n^n=\sum\limits_{i=0}^{n}\mathrm{C}_n^i\)）；这里使用深度优先搜索输出组合，算法的时间复杂度可以降低到 \(O(\mathrm{C}_n^1+\mathrm{C}_n^2+...+\mathrm{C}_n^m)\)，也就是\(O(\sum\limits_{i=1}^{m}\mathrm{C}_n^i)\)，如果循环条件更严格地限制为：m-k+i<=n，还能进一步提高效率。
如果要输出 1～\(n\) 这 \(n\) 个数的所有非空子集，可以用下面的搜索策略实现：
#include<iostream>
using namespace std;
const int MAX = 20;
//n定义成全局变量
int n,cnt = 0;
//ans用来记录组合的一种方案
int ans[MAX+1];
//搜索第k个数用哪一个数
void dfs(int k){
if(k==n+1){ //现在考虑到了第n+1个数用哪个数字，已经到达“目的地”（递归出口）
return;
}
//第k个数可以用ans[k-1]+1～n的任意一个数i
for(int i=ans[k-1]+1;i<=n;i++){
ans[k] = i; //第k个数用i，记录到ans数组中
cnt++;
//输出选出k个数的一个方案
for(int j=1;j<=k;j++){
cout<<ans[j]<<" ";
}
cout<<endl;
dfs(k+1); //在第k个数用i的基础上，继续搜索第k+1个数用哪一个数字
}
}
int main(){
cin>>n;
//主函数只需要调用dfs(1)，以“考虑第1个数用哪一个数”为搜索起点
dfs(1);
cout<<"Total:"<<cnt<<endl; //这里会输出 2^n-1
return 0;
} 2.通过参数指定枚举起始值
此外，还可以增加一个参数来指定枚举起始值，下面是用此策略输出组合和输出所有非空子集的参考代码：
#include<iostream>
using namespace std;
int n,m,ans[11];
//搜索第k个数，从start开始枚举其取值
void dfs(int k,int start){
if(k==m+1){
for(int j=1;j<=m;j++)
cout<<ans[j]<<" ";
cout<<endl;
}
for(int i=start;i<=n;i++){
ans[k] = i;
//下个数要用i后面的数，从i+1开始枚举
dfs(k+1,i+1);
}
}
int main()
{
cin>>n>>m;
dfs(1,1);
return 0;
}//输出所有非空子集
#include<iostream>
using namespace std;
int n,ans[11];
//搜索第k个数，从start开始枚举其取值
void dfs(int k,int start){
for(int i=start;i<=n;i++){
ans[k] = i;
for(int j=1;j<=k;j++)
cout<<ans[j]<<" ";
cout<<endl;
//下个数要用i后面的数，从i+1开始枚举
dfs(k+1,i+1);
}
}
int main()
{
cin>>n;
dfs(1,1);
return 0;
}3.由输入的数据生成组合
如果是输入 \(n\) 个数（不存在相同的数），要选择 \(m\) 个数，简单修改上面的程序就能实现：
#include<iostream>
using namespace std;
const int MAX = 20;
//n、m定义成全局变量
int n,m;
//ans用来记录组合的一种方案（记录了取自数组a的元素下标）
int a[MAX+1],ans[MAX+1];
//搜索第k个数用哪一个数
void dfs(int k){
if(k==m+1){ //现在考虑到了第m+1个数用哪个数字，已经到达“目的地”（递归出口）
//输出搜索出来的一个组合方案（方案保存在ans数组中）
for(int i=1;i<=m;i++) cout<<a[ans[i]]<<" ";
cout<<endl;
return;
}
//第k个数可以用数组a中的第ans[k-1]+1～n的任意一个数
for(int i=ans[k-1]+1;m-k+i<=n;i++){
ans[k] = i; //第k个数用数组a中的第i个数，记录到ans数组中
dfs(k+1); //在第k个数用数组a中的第i个数的基础上，继续搜索第k+1个数用哪一个数字
}
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i];
dfs(1);
return 0;
} 4.组合去重
如果输入的供选择的 \(n\) 个数中有相同的数，可知上面的搜索策略会出现重复的组合情况。可以采用下面的搜索策略避免出现重复：
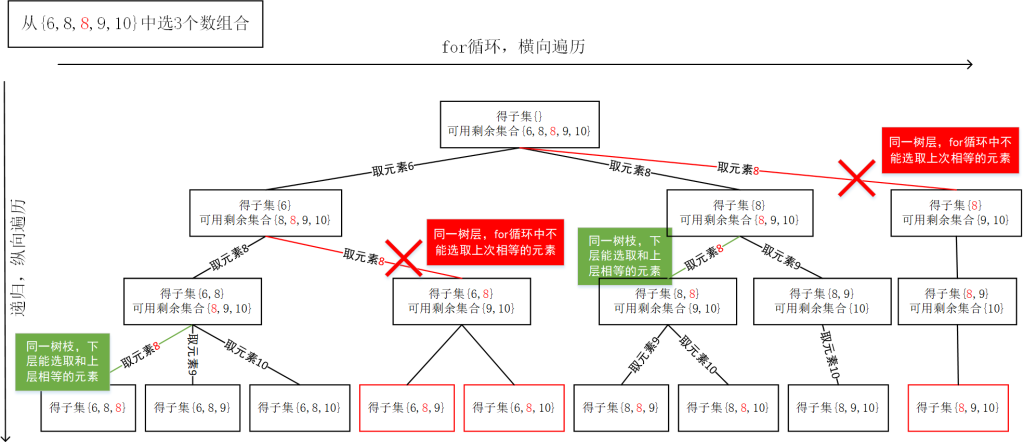
//当要选择的数中有相同的数，本程序能够保证搜索出来的【组合】不重复
#include<iostream>
#include<algorithm>
using namespace std;
const int MAX = 20;
//n、m定义成全局变量
int n,m;
//ans用来记录组合的一种方案（记录了取自数组a的元素下标）
int a[MAX+1],ans[MAX+1],used[MAX+1];
//搜索第k个数用哪一个数
void dfs(int k){
if(k==m+1){ //现在考虑到了第m+1个数用哪个数字，已经到达“目的地”（递归出口）
//输出搜索出来的一个组合方案（方案保存在ans数组中）
for(int i=1;i<=m;i++) cout<<a[ans[i]]<<" ";
cout<<endl;
return;
}
//第k个数可以用数组a中的第ans[k-1]+1～n的任意一个数
for(int i=ans[k-1]+1;m-k+i<=n;i++){
//当前枚举的数a[i]和上一次枚举的数a[i-1]相同，如果a[i-1]当前没有被使用，说明是同一树层，此时不能继续搜索
if(i>1 && a[i]==a[i-1] && !used[i-1]) continue;
ans[k] = i; //第k个数用数组a中的第i个数，记录到ans数组中
used[i] = 1;
dfs(k+1); //在第k个数用数组a中的第i个数的基础上，继续搜索第k+1个数用哪一个数字
used[i] = 0;
}
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i];
sort(a+1,a+n+1); //搜索前必须排序
dfs(1);
return 0;
} \(n\) 选 \(m\) 的排列去重方案可以参照上面 \(n\) 选 \(m\) 的组合去重方案实现：//当要选择的数中有相同的数，本程序能够保证搜索出来的【排列】不重复
#include<iostream>
#include<algorithm>
using namespace std;
const int MAX = 20;
//n、m定义成全局变量
int n,m;
//ans用来记录排列的一种方案（记录了取自数组a的元素下标）
int a[MAX+1],ans[MAX+1],used[MAX+1];
//搜索第k个位置用哪一个数
void dfs(int k){
if(k==m+1){ //现在考虑到了第m+1个位置用哪个数字，已经到达“目的地”（递归出口）
//输出搜索出来的一个排列方案（方案保存在ans数组中）
for(int i=1;i<=m;i++) cout<<a[ans[i]]<<" ";
cout<<endl;
return;
}
//第k个位置可以用数组a中的第1～n的任意一个数
for(int i=1;i<=n;i++){
if(used[i]) continue;
//当前枚举的数a[i]和上一次枚举的数a[i-1]相同，如果a[i-1]当前没有被使用，说明是同一树层，此时不能继续搜索
if(i>1 && a[i]==a[i-1] && !used[i-1]) continue;
ans[k] = i; //第k个数用数组a中的第i个数，记录到ans数组中
used[i] = 1;
dfs(k+1); //在第k个数用数组a中的第i个数的基础上，继续搜索第k+1个数用哪一个数字
used[i] = 0;
}
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i];
sort(a+1,a+n+1); //搜索前必须排序
dfs(1);
return 0;
}五、走迷宫
问题：P1605 迷宫
1.全局变量记录搜索过程中的坐标
直接套用DFS框架，可以使用全局变量记录搜索过程中经过的坐标点\((cx,cy)\)：
#include<iostream>
using namespace std;
const int MAX = 10;
//迷宫尺寸
int n,m;
//起点坐标(sx,sy)，终点坐标(fx,fy)，搜索过程中的动态坐标(cx,cy)
int sx,sy,fx,fy,cx,cy;
//ans记录方案数
int ans = 0;
//space数组记录迷宫里所有点的情况：1-障碍，0-通畅
int space[MAX][MAX];
//used数组记录搜索过程中点是否被使用过
int used[MAX][MAX];
//四个方向移动x,y变化值
int dirs[4][2] = {
{-1,0},
{0,-1},
{1,0},
{0,1}
};
//搜索第k步的走法（其实本问题函数可以不用参数）
void dfs(int k){
if(cx==fx && cy==fy){ //到达终点，方案数+1
ans++;
return;
}
//对四个方向搜索
for(int i=0;i<4;i++){
//计算下一个坐标点
int nx = cx+dirs[i][0];
int ny = cy+dirs[i][1];
//坐标点(nx,ny)在迷宫内、不是障碍、没有被使用过
if(nx>=1 && nx<=n && ny>=1 && ny<=m &&
!space[nx][ny] && !used[nx][ny]){
used[nx][ny] = 1; //标记被使用
int lx = cx,ly = cy; //记录下当前坐标
cx = nx,cy = ny;
dfs(k+1); //继续搜索第k+1步走法
used[nx][ny] = 0; //恢复为没有被使用
cx = lx,cy = ly; //恢复坐标
}
}
}
int main(){
int t,x,y;
cin>>n>>m>>t;
cin>>sx>>sy>>fx>>fy;
//标记障碍
while(t--){
cin>>x>>y;
space[x][y] = 1;
}
cx = sx,cy = sy;
used[sx][sy] = 1; //标记起点被使用
dfs(1); //搜索第1步的走法
cout<<ans<<endl;
return 0;
} 2.函数参数记录搜索过程中的坐标
还可以对dfs递归函数的参数重新设计——void dfs(int x,int y)——表示从坐标点\((x,y)\)开始搜索：
#include<iostream>
using namespace std;
const int MAX = 10;
//迷宫尺寸
int n,m;
//起点坐标(sx,sy)，终点坐标(fx,fy)
int sx,sy,fx,fy;
//ans记录方案数
int ans = 0;
//space数组记录迷宫里所有点的情况：1-障碍，0-通畅
int space[MAX][MAX];
//used数组记录搜索过程中点是否被使用过
int used[MAX][MAX];
//四个方向移动x,y变化值
int dirs[4][2] = {
{-1,0},
{0,-1},
{1,0},
{0,1}
};
//从坐标点(x,y)开始搜索
void dfs(int x,int y){
if(x==fx && y==fy){ //到达终点，方案数+1
ans++;
return;
}
//对四个方向搜索
for(int i=0;i<4;i++){
//计算下一个坐标点
int nx = x+dirs[i][0];
int ny = y+dirs[i][1];
//坐标点(nx,ny)在迷宫内、不是障碍、没有被使用过
if(nx>=1 && nx<=n && ny>=1 && ny<=m &&
!space[nx][ny] && !used[nx][ny]){
used[nx][ny] = 1; //标记被使用
dfs(nx,ny); //对坐标点(nx,ny)继续展开搜索
used[nx][ny] = 0; //恢复为没有被使用
}
}
}
int main(){
int t,x,y;
cin>>n>>m>>t;
cin>>sx>>sy>>fx>>fy;
//标记障碍
while(t--){
cin>>x>>y;
space[x][y] = 1;
}
used[sx][sy] = 1; //标记起点被使用
dfs(sx,sy); //从起点开始搜索
cout<<ans<<endl;
return 0;
} 3.输出方案途径的坐标点
现在提出新的要求，在输出方案数前，先输出每一种方案的具体路径（途径的所有坐标点）。可以开一个二维全局数组int roads[MAX*MAX][2];用来记录方案的路径，极限情况下一条路径通过迷宫所有点，所以二维数组第一维长度可以设置为MAX*MAX。另外搜索函数再添加一个参数k来记录当前是第几步，这样也能方便将搜索到的坐标点\((nx,ny)\)记录到roads[k]中：
#include<iostream>
using namespace std;
const int MAX = 10;
//迷宫尺寸
int n,m;
//起点坐标(sx,sy)，终点坐标(fx,fy)
int sx,sy,fx,fy;
//ans记录方案数
int ans = 0;
//space数组记录迷宫里所有点的情况：1-障碍，0-通畅
int space[MAX][MAX];
//used数组记录搜索过程中点是否被使用过
int used[MAX][MAX];
//roads数组记录路径
int roads[MAX*MAX][2];
//四个方向移动x,y变化值
int dirs[4][2] = {
{-1,0},
{0,-1},
{1,0},
{0,1}
};
//从坐标点(x,y)开始搜索第k步走法
void dfs(int x,int y,int k){
if(x==fx && y==fy){ //到达终点，方案数+1
ans++;
//输出路径
cout<<"("<<sx<<","<<sy<<")";
for(int i=1;i<k;i++){
cout<<"->("<<roads[i][0]<<","<<roads[i][1]<<")";
}
cout<<endl;
return;
}
//对四个方向搜索
for(int i=0;i<4;i++){
//计算下一个坐标点
int nx = x+dirs[i][0];
int ny = y+dirs[i][1];
//坐标点(nx,ny)在迷宫内、不是障碍、没有被使用过
if(nx>=1 && nx<=n && ny>=1 && ny<=m &&
!space[nx][ny] && !used[nx][ny]){
used[nx][ny] = 1; //标记被使用
roads[k][0] = nx; //记录路径
roads[k][1] = ny;
dfs(nx,ny,k+1); //对坐标点(nx,ny)继续展开搜索
used[nx][ny] = 0; //恢复为没有被使用
}
}
}
int main(){
int t,x,y;
cin>>n>>m>>t;
cin>>sx>>sy>>fx>>fy;
//标记障碍
while(t--){
cin>>x>>y;
space[x][y] = 1;
}
used[sx][sy] = 1; //标记起点被使用
dfs(sx,sy,1); //从起点开始搜索第1步走法
cout<<ans<<endl;
return 0;
} 上面的程序已经使用全局数组来记录每一步的坐标，那么可以在搜索函数中直接使用roads数组来计算坐标，可以省略描述搜索坐标的参数x、y：
#include<iostream>
using namespace std;
const int MAX = 10;
//迷宫尺寸
int n,m;
//起点坐标(sx,sy)，终点坐标(fx,fy)
int sx,sy,fx,fy;
//ans记录方案数
int ans = 0;
//space数组记录迷宫里所有点的情况：1-障碍，0-通畅
int space[MAX][MAX];
//used数组记录搜索过程中点是否被使用过
int used[MAX][MAX];
//roads数组记录路径
int roads[MAX*MAX][2];
//四个方向移动x,y变化值
int dirs[4][2] = {
{-1,0},
{0,-1},
{1,0},
{0,1}
};
//搜索第k步走法，上一步坐标是(roads[k-1][0],roads[k-1][1])
void dfs(int k){
if(roads[k-1][0]==fx && roads[k-1][1]==fy){ //到达终点，方案数+1
ans++;
//输出路径
cout<<"("<<sx<<","<<sy<<")";
for(int i=1;i<k;i++){
cout<<"->("<<roads[i][0]<<","<<roads[i][1]<<")";
}
cout<<endl;
return;
}
//对四个方向搜索
for(int i=0;i<4;i++){
//计算下一个坐标点
int nx = roads[k-1][0]+dirs[i][0];
int ny = roads[k-1][1]+dirs[i][1];
//坐标点(nx,ny)在迷宫内、不是障碍、没有被使用过
if(nx>=1 && nx<=n && ny>=1 && ny<=m &&
!space[nx][ny] && !used[nx][ny]){
used[nx][ny] = 1; //标记被使用
roads[k][0] = nx; //记录路径
roads[k][1] = ny;
dfs(k+1); //继续搜索第k+1步走法
used[nx][ny] = 0; //恢复为没有被使用
}
}
}
int main(){
int t,x,y;
cin>>n>>m>>t;
cin>>sx>>sy>>fx>>fy;
//标记障碍
while(t--){
cin>>x>>y;
space[x][y] = 1;
}
used[sx][sy] = 1; //标记起点被使用
roads[0][0] = sx; //记录起点坐标
roads[0][1] = sy;
dfs(1); //从起点开始搜索第1步走法
cout<<ans<<endl;
return 0;
} 4.寻找最优策略(步数最少)
现在求解另一个问题，从起点到终点的所有走法中，至少要经过几个坐标点（包括起点和终点，如果没有任何路径输出-1）。和上面思路一致，搜索用的递归函数仍然要设计第三个参数k，搜到终点的时候k就是路径经过的坐标点数，通过打擂台的方式求出最小值即可：
#include<iostream>
using namespace std;
const int MAX = 10;
//迷宫尺寸
int n,m;
//起点坐标(sx,sy)，终点坐标(fx,fy)
int sx,sy,fx,fy;
//ans记录方案数
int ans = 0;
//minstep记录路径途径最少坐标点数
int minstep;
//space数组记录迷宫里所有点的情况：1-障碍，0-通畅
int space[MAX][MAX];
//used数组记录搜索过程中点是否被使用过
int used[MAX][MAX];
//四个方向移动x,y变化值
int dirs[4][2] = {
{-1,0},
{0,-1},
{1,0},
{0,1}
};
//从坐标点(x,y)开始搜索第k步走法
void dfs(int x,int y,int k){
if(x==fx && y==fy){ //到达终点，方案数+1
ans++;
if(k<minstep) minstep = k;
return;
}
//对四个方向搜索
for(int i=0;i<4;i++){
//计算下一个坐标点
int nx = x+dirs[i][0];
int ny = y+dirs[i][1];
//坐标点(nx,ny)在迷宫内、不是障碍、没有被使用过
if(nx>=1 && nx<=n && ny>=1 && ny<=m &&
!space[nx][ny] && !used[nx][ny]){
used[nx][ny] = 1; //标记被使用
dfs(nx,ny,k+1); //对坐标点(nx,ny)继续展开搜索
used[nx][ny] = 0; //恢复为没有被使用
}
}
}
int main(){
int t,x,y;
cin>>n>>m>>t;
cin>>sx>>sy>>fx>>fy;
minstep = n*m;
//标记障碍
while(t--){
cin>>x>>y;
space[x][y] = 1;
}
used[sx][sy] = 1; //标记起点被使用
dfs(sx,sy,1); //从起点开始搜索第1步走法
cout<<(ans?minstep:-1)<<endl;
return 0;
}