一、数的拆分
问题:任何一个大于 1 的自然数 \(n\),总可以拆分成若干个小于 \(n\) 的自然数的和。例如当 \(n=7\) 时,一共有 14 种拆分方法:
7=1+1+1+1+1+1+1 7=1+1+1+1+1+2 7=1+1+1+1+3 7=1+1+1+2+2 7=1+1+1+4 7=1+1+2+3 7=1+1+5 7=1+2+2+2 7=1+2+4 7=1+3+3 7=1+6 7=2+2+3 7=2+5 7=3+4 total=14
输入自然数 \(n\),按照上面的格式输出拆分方案和方案种数。
分析:使用深度优先搜索算法,对于自然数 \(n\),拆分出来一个整数 \(i\)(\(1<=i<n\))之后,可以用同样的策略继续拆分 \(n-i\)。搜索函数可以设计成 void dfs(int s,int k);,参数 s 表示对自然数 s 拆分,参数 k 表示是整个问题的第 k 次拆分(借助 k 可以很方便地将本次拆出来的数存放到用来记录具体拆分方案的数组中):
#include<iostream>
using namespace std;
const int MAX = 100;
int n;
int ans[MAX+1]; //记录具体拆分方案
int cnt = 0; //方案总数
//输出具体方案
void output(int k){
cout<<n<<"="<<ans[1];
for(int i=2;i<k;i++) cout<<"+"<<ans[i];
cout<<endl;
}
//对s拆分,是整个问题的第k次拆分
void dfs(int s,int k){
if(s==0){
cnt++;
output(k);
return;
}
//粗略来看:第k次拆出来的数可以是ans[k-1]~s中的任意一个自然数
//考虑到k==1时,ans[0]==0,起始值修正为max(1,ans[k-1])
//拆出来的数必须小于n,终止值修正为min(n-1,s)
for(int i=max(1,ans[k-1]);i<=min(n-1,s);i++){
ans[k] = i; //记录第k次拆除来的数i
dfs(s-i,k+1); //继续对s-i拆分,是整个问题的第k+1次拆分
}
}
int main(){
cin>>n;
dfs(n,1); //对n拆分,第1次拆分
cout<<"total="<<cnt<<endl;
return 0;
}
其实也可以将 s、k 设置成全局变量,那么dfs函数可以不带参数,但是要注意在递归调用前要修改 s、k 的值,在递归调用后回溯时要恢复 s、k 的值:
#include<iostream>
using namespace std;
const int MAX = 100;
int n,s,k;
int ans[MAX+1]; //记录具体拆分方案
int cnt = 0; //方案总数
//输出具体方案
void output(int k){
cout<<n<<"="<<ans[1];
for(int i=2;i<k;i++) cout<<"+"<<ans[i];
cout<<endl;
}
//借助全局变量记录s和k,dfs函数无参数
void dfs(){
if(s==0){
cnt++;
output(k);
return;
}
//粗略来看:第k次拆出来的数可以是ans[k-1]~s中的任意一个自然数
//考虑到k==1时,ans[0]==0,起始值修正为max(1,ans[k-1])
//拆出来的数必须小于n,终止值修正为min(n-1,s)
for(int i=max(1,ans[k-1]);i<=min(n-1,s);i++){
ans[k] = i; //记录第k次拆除来的数i
s -= i, k++; //修改全局变量的值
dfs();
s += i, k--; //恢复全局变量的值
}
}
int main(){
cin>>n;
s = n;
k = 1;
dfs();
cout<<"total="<<cnt<<endl;
return 0;
}
二、八皇后问题
问题:在 \(n \times n\) 的国际象棋上放 \(n\) 个皇后,使任意两个皇后之间不能互吃。已知国际象棋规则中,皇后能吃同一行、同一列、同一对角线上的任意棋子。
分析:使用DFS来搜索每一行皇后的放置位置,算法框架如下:
//放置第x行的皇后
void dfs(int x){
if(x==n+1){
//输出方案
return;
}
//粗略来看:第x行的皇后可以放在1~n列的任意位置
for(int y=1;y<=n;y++){
if(第y列上没有皇后 && (x,y)处的两条对角线上没有皇后){
//记录下第x行皇后放在第y列
//对放置皇后的位置进行标记
dfs(x+1);
//恢复放置皇后的位置的标记
}
}
}
因为是通过搜索依次考虑第 1 行,第 2 行,...,第 \(n\) 行皇后放置的位置,每一行上只能有一个皇后,所以搜索过程中放置皇后时只需要考虑“第 \(y\) 列上没有皇后 && \((x,y)\) 处的两条对角线上没有皇后”。可以设置一个全局数组 a[n] 来标记搜索过程中列的占用情况,如果 a[y]==0 就能判断“第 \(y\) 列上没有皇后”。那么如何判断“\((x,y)\) 处的两条对角线上没有皇后”呢?其实对角线上的点 \((x,y)\) 存在一定的特性:
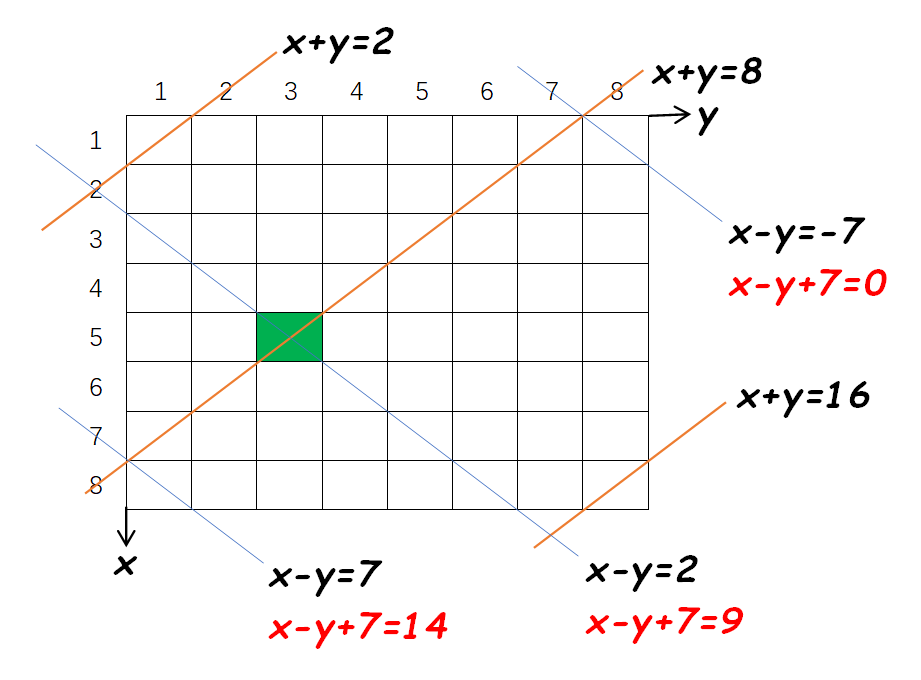
在 \(45^o\) 方向上的某条对角线(上图中黄色对角线)上任意一点 \(x+y\) 是一个定值,所有黄色对角线从上到下这个定值依次是 2、3、...、16(最大值是 \(2n\))。可以设置一个数组 b[2*n+1] 来标记黄色对角线的占用情况,例如上图所示第 5 行第 3 列(\(x=5,y=3,x+y=8\))放置了皇后,将 b[8] 赋值成 1 表示占用,那么第 6 行放置皇后时,考虑第 2 列(\(x=6,y=2,x+y=8\))会发现 b[8]!=0,则不能放在第 2 列;
在 \(135^o\) 方向上的某条对角线(上图中蓝色对角线)上任意一点 \(x-y\) 是一个定值,所有蓝色对角线从上到下这个定值依次是 -7、-6、...、7。如果采用上面类似的策略,数组下标会出现负数,那么可以考虑 \(x-y+7\)(也就是 \(x-y+n-1\))也是定值,并且所有蓝色对角线从上到下这个定值依次是 0、1、...、14(最大值是 \(2n-2\))。可以设置一个数组 c[2*n-1] 来标记蓝色对角线的占用情况,例如上图所示第 5 行第 3 列(\(x=5,y=3,x-y+7=9\))放置了皇后,将 c[9] 赋值成 1 表示占用,那么第 6 行放置皇后时,考虑第 4 列(\(x=6,y=4,x-y+7=9\))会发现 c[9]!=0,则不能放在第 4 列。
通过上述分析,解决 \(n\) 皇后的参考代码如下:
#include<iostream>
using namespace std;
const int MAX = 20;
int n;
int ans[MAX+1]; //记录具体方案(每一行放在哪一列)
int a[MAX+1],b[2*MAX+1],c[2*MAX-1];
int cnt = 0; //方案总数
//输出具体方案
void output(){
//输出n*n的棋盘皇后放置情况
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(ans[i]==j) cout<<"*";
else cout<<"-";
}
cout<<endl;
}
cout<<endl;
}
//放置第x行的皇后
void dfs(int x){
if(x==n+1){
cnt++;
output();
return;
}
//粗略来看:第x行的皇后可以放在1~n列的任意位置
for(int y=1;y<=n;y++){
if(!a[y] && !b[x+y] && !c[x-y+n-1]){ //列、两条对角线没有被占用
//记录下第x行皇后放在第y列
ans[x] = y;
//对放置皇后的位置进行标记(列、两条对角线)
a[y] = b[x+y] = c[x-y+n-1] = 1;
dfs(x+1);
//恢复放置皇后的位置的标记(列、两条对角线)
a[y] = b[x+y] = c[x-y+n-1] = 0;
}
}
}
int main(){
cin>>n;
dfs(1); //从放“第1行皇后”开始搜索
cout<<"total="<<cnt<<endl;
return 0;
}
本问题也可以通过搜索每一列皇后放置情况来解决,读者可以自行完成。
三、向右跳的马
问题:有一个 \(n \times m\) 的棋盘,棋盘左下角坐标为 \((0,0)\),右上角坐标为 \((n,m)\)。马从 \((0,0)\) 出发,每次只能向右跳,输出所有跳到 \((n,m)\) 的跳法。
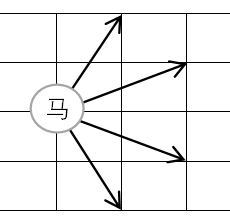
分析:搜索并记录马每次跳的坐标点。马每次只能向右跳,可知在搜索过程中不会出现跳回到之前搜索过的点的情况,那就不需要像走迷宫问题那样借助数组来避免跳到之前跳过的点。马从 \((0,0)\) 出发,最多跳 \(m\) 次就能到达第 \(m\) 列,所以记录具体跳跃路径数组的长度开到 \(m\) 即可。
#include<iostream>
using namespace std;
const int MAX = 20;
int n,m;
int ans[MAX+1][2]; //记录跳跃路径坐标点
int dirs[4][2]={ //马向右4种跳法x,y坐标增量
{2,1},
{1,2},
{-1,2},
{-2,1}
};
//第k次跳跃
void dfs(int k){
if(ans[k-1][0]==n && ans[k-1][1]==m){
cout<<"("<<ans[0][0]<<","<<ans[0][1]<<")";
for(int i=1;i<k;i++) cout<<"->("<<ans[i][0]<<","<<ans[i][1]<<")";
cout<<endl;
return;
}
//向右跳的4种方法
for(int i=0;i<4;i++){
//计算跳过去的坐标
int nx = ans[k-1][0]+dirs[i][0];
int ny = ans[k-1][1]+dirs[i][1];
//在棋盘内
if(nx>=0 && nx<=n && ny>=0 && ny<=m){
ans[k][0] = nx;
ans[k][1] = ny;
dfs(k+1); //搜索第k+1次跳
}
}
}
int main(){
cin>>n>>m;
//记录下开始坐标(第0次跳)
ans[0][0] = ans[0][1] = 0;
dfs(1); //从第1次跳跃开始搜索
return 0;
}
换用DFS另一个模版,就是在递归调用前判断是否到目的地,如果到目的地输出解,否则才递归调用:
#include<iostream>
using namespace std;
const int MAX = 20;
int n,m;
int ans[MAX+1][2]; //记录跳跃路径坐标点
int dirs[4][2]={ //马向右4种跳法x,y坐标增量
{2,1},
{1,2},
{-1,2},
{-2,1}
};
//第k次跳跃
void dfs(int k){
//向右跳的4种方法
for(int i=0;i<4;i++){
//计算跳过去的坐标
int nx = ans[k-1][0]+dirs[i][0];
int ny = ans[k-1][1]+dirs[i][1];
//在棋盘内
if(nx>=0 && nx<=n && ny>=0 && ny<=m){
ans[k][0] = nx;
ans[k][1] = ny;
if(ans[k][0]==n && ans[k][1]==m){ //到达目的地
cout<<"("<<ans[0][0]<<","<<ans[0][1]<<")";
for(int i=1;i<=k;i++)
cout<<"->("<<ans[i][0]<<","<<ans[i][1]<<")";
cout<<endl;
}else{
dfs(k+1); //搜索第k+1次跳
}
}
}
}
int main(){
cin>>n>>m;
//记录下开始坐标(第0次跳)
ans[0][0] = ans[0][1] = 0;
dfs(1); //从第1次跳跃开始搜索
return 0;
}
四、跳马问题
问题:和上面问题一样,马从 \((0,0)\) 出发,不过取消只能往右跳的限制,输出用最少次数跳遍棋盘所有点的方案。
分析:马要用最少次数跳遍所有点,可以转换成从 \((0,0)\) 出发搜索马跳跃次数恰好达到 \((n+1)(m+1)\) 次(这样就用最少次数跳遍了棋盘所有的点)的所有情况,这里需要使用全局数组记录搜索过程中跳过的点。
#include<cstdio>
using namespace std;
const int MAX = 20;
int n,m,total;
int ans[MAX+1][MAX+1]; //记录每个坐标点跳跃次序
int visited[MAX+1][MAX+1]; //记录搜索过程中某点是否已经跳过
int dirs[8][2]={ //马8种跳法x,y坐标增量
{2,-1},
{1,-2},
{-1,-2},
{-2,-1},
{2,1},
{1,2},
{-1,2},
{-2,1}
};
//在(x,y)处搜索第k次跳跃
void dfs(int x,int y,int k){
if(k==total+1){
//输出方案,注意输出时和题意一致,确保(0,0)在左下角
for(int i=n;i>=0;i--){
for(int j=0;j<=m;j++){
printf("%4d",ans[i][j]);
}
printf("\n");
}
printf("\n");
return;
}
//8种方法
for(int i=0;i<8;i++){
//计算跳过去的坐标
int nx = x+dirs[i][0];
int ny = y+dirs[i][1];
//在棋盘内
if(nx>=0 && nx<=n && ny>=0 && ny<=m && !visited[nx][ny]){
ans[nx][ny] = k;
visited[nx][ny] = 1;
dfs(nx,ny,k+1); //在(nx,ny)处搜索第k+1次跳跃
visited[nx][ny] = 0;
}
}
}
int main(){
scanf("%d%d",&n,&m);
total = (n+1)*(m+1);
//开始坐标处记录下第1跳
ans[0][0] = 1;
visited[0][0] = 1;
dfs(0,0,2); //在(0,0)处搜索第2次跳跃
return 0;
}
五、四阶数独
数独是一种著名的益智游戏。这里讨论一种简化的数独——四阶数独。给定 \(4 \times 4\) 的格子,每个格子里只能填写 1~4 之间的数字,要求每行、每列和四等分更小的正方形内部都恰好由 1~4 组成。如下图所示是一个合法的四阶数独:
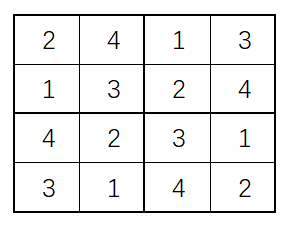
现在给出空白的方格,问一共有多少种合法的填写方法?
分析:使用DFS来解决问题,对 16 个小方格从左上角开始按行编号,搜索每个方格填写的数字。为了让方案合法,那么需要考虑题目中提出的“每行、每列和四等分更小的正方形内部都恰好由 1~4 组成”这一特殊要求,其实就是在每行、每列和四等分更小的正方形内部不能出现相同的数字,和上面介绍的搜索策略相同,使用标记数组来标记数字占用情况即可。
那么对于编号为 \(k\) 的小方格,需要计算其所在的行编号、列编号和四等分小正方形的编号,其实可以通过简单的计算得出:
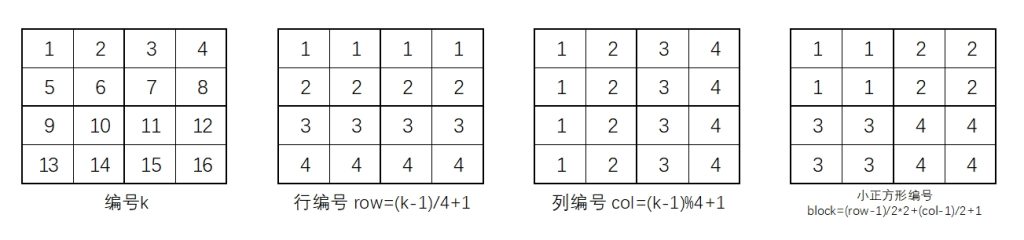
使用DFS框架,参考程序如下:
#include<iostream>
using namespace std;
const int MAX = 4;
const int n = MAX*MAX;
int ans[n+1],cnt = 0;
int a[MAX+1][MAX+1],b[MAX+1][MAX+1],c[MAX+1][MAX+1];
//第k个小方格填写哪一个数字
void dfs(int k){
if(k>n){
cnt++;
for(int i=1;i<=n;i++){
cout<<ans[i]<<" ";
if(i%4==0) cout<<endl;
}
cout<<endl;
return;
}
int row = (k-1)/4+1; //计算行编号
int col = (k-1)%4+1; //计算列编号
int block = (row-1)/2*2+(col-1)/2+1; //计算小正方形编号
//粗略来看:1~4四个数字都可以填写
for(int i=1;i<=4;i++){
//第row行、第col列、第block个小正方形内没有填写数字i才能填写
if(!a[row][i] && !b[col][i] && !c[block][i]){
ans[k] = i;
a[row][i] = b[col][i] = c[block][i] = 1;
dfs(k+1);
a[row][i] = b[col][i] = c[block][i] = 0;
}
}
}
int main(){
dfs(1);
cout<<cnt<<endl;
return 0;
}
还可以搜索第 row 行 col 列方格填数情况:
#include<iostream>
using namespace std;
const int MAX = 4;
const int n = MAX*MAX;
int ans[MAX+1][MAX+1],cnt = 0;
int a[MAX+1][MAX+1],b[MAX+1][MAX+1],c[MAX+1][MAX+1];
//第row行col列个小方格填写哪一个数字
void dfs(int row,int col){
if(row==5){
cnt++;
for(int i=1;i<=4;i++){
for(int j=1;j<=4;j++){
cout<<ans[i][j]<<" ";
}
cout<<endl;
}
cout<<endl;
return;
}
int block = (row-1)/2*2+(col-1)/2+1; //计算小正方形编号
//粗略来看:1~4四个数字都可以填写
for(int i=1;i<=4;i++){
//第row行、第col列、第block个小正方形内没有填写数字i才能填写
if(!a[row][i] && !b[col][i] && !c[block][i]){
ans[row][col] = i;
a[row][i] = b[col][i] = c[block][i] = 1;
if(col+1==5) dfs(row+1,1);
else dfs(row,col+1);
a[row][i] = b[col][i] = c[block][i] = 0;
}
}
}
int main(){
dfs(1,1);
cout<<cnt<<endl;
return 0;
}
六、P2392 考前临时抱佛脚

分析:由于只能一科一科地完成作业,所以每个科目独立处理即可。现在考虑一个科目的情况。对于一个科目,需要分成两组,当这两组分别耗时总和最接近时,完成这一科作业的耗时最小,否则一边大脑是闲置的,没有做到合理分配。因此,只需要从该科目作业中取出一部分,使这些题目的总耗时不超过这个科目总耗时的一半并且这部分的总耗时要尽可能的大,这样就将这个科目的题目划分成了耗时尽可能均等的两个部分。
这是一个典型的子集枚举问题(取或不取),对于每一道题目,需要搜索选取或者不选取两种情况,还可以添加一个参数来记录搜索过程中已经选取的所有题目耗时总和。
#include<iostream>
using namespace std;
const int MAX = 4;
int n,sum,ans;
int cnt[MAX+1],a[21];
//搜索是否取第k道题目,所有取的题目耗时和为s
void dfs(int k,int s){
if(k==n+1){
//越接近总耗时的一半越好,所以取所有方案的最大值
if(s>ans) ans = s;
return;
}
//取第k道题目(取后所有取的题目的耗时和不能超过总耗时的一半)
if(s+a[k]<=sum/2) dfs(k+1,s+a[k]);
//不取第k道题目
dfs(k+1,s);
}
int main(){
for(int i=1;i<=MAX;i++) cin>>cnt[i];
int total = 0;
for(int i=1;i<=MAX;i++){
sum = ans = 0; //清0
n = cnt[i]; //全局变量n赋值为当前科目题目总数
//输入每题耗时,计算总耗时
for(int j=1;j<=n;j++) cin>>a[j],sum+=a[j];
dfs(1,0); //从“是否取第1题”开始搜索
total += sum-ans; //ans非常接近sum的一半,sum-ans就是本科作业耗时
}
cout<<total<<endl;
return 0;
}
还可以使用前面介绍的子集枚举策略,枚举所有非空子集,算法效率和上面搜索策略相同:
#include<iostream>
using namespace std;
const int MAX = 4;
int n,sum,ans;
int cnt[MAX+1],result[21],a[21];
//搜索所有非空子集
void dfs(int k,int s){
if(k==n+1){
return;
}
for(int i=result[k-1]+1;i<=n;i++){
if(s+a[i]<=sum/2){
result[k] = i;
dfs(k+1,s+a[i]);
ans = max(ans,s+a[i]);
}
}
}
int main(){
for(int i=1;i<=MAX;i++) cin>>cnt[i];
int total = 0;
for(int i=1;i<=MAX;i++){
sum = ans = 0; //清0
n = cnt[i]; //全局变量n赋值为当前科目题目总数
//输入每题耗时,计算总耗时
for(int j=1;j<=n;j++) cin>>a[j],sum+=a[j];
dfs(1,0); //从“第一题选哪一道题目开始”开始搜索
total += sum-ans; //ans非常接近sum的一半,sum-ans就是本科作业耗时
}
cout<<total<<endl;
return 0;
}
 NOIP学习小站
NOIP学习小站