搜索与回溯算法（3）——剪枝

DFS算法通过在函数内使用循环枚举下一步（或者是当前步）的所有情况，并在循环体中递归调用函数，实现了在当前基础上进一步搜索。如果根据题意可以严格限制循环枚举的条件（减少循环枚举的次数）或者在循环体中额外添加更全面的进一步递归搜索的条件，这两种做法都可以有效减少递归调用的次数，提高程序的运行效率，这样的搜索技巧形象地称为剪枝。

void dfs(int k){
	if(到达目的地){
		输出解;
		return;
	}
	for(枚举下一步的每一种情况){     //减少循环枚举次数
		if(满足条件){              //设置更严格的条件
			保存结果;
			dfs(k+1);
			恢复到保存结果之前的状态（回溯一步） 
		}
	} 
} 

一、输出组合

前面介绍了组合数，也就是：从 1～\(n\) 这 \(n\) 个整数选择 \(m\) 个不同的数构成组合，输出所有的组合情况。

来看前面给出的参考代码：

#include<iostream>
using namespace std;
const int MAX = 20;
 
//n、m定义成全局变量
int n,m;
//ans用来记录组合的一种方案 
int ans[MAX+1];

//搜索第k个数用哪一个数 
void dfs(int k){
    if(k==m+1){    //现在考虑到了第m+1个数用哪个数字，已经到达“目的地”（递归出口）
        //输出搜索出来的一个组合方案（方案保存在ans数组中） 
        for(int i=1;i<=m;i++) cout<<ans[i]<<" ";
        cout<<endl;
        return;
    }
    //第k个数可以用ans[k-1]+1～n的任意一个数i 
    for(int i=ans[k-1]+1;i<=n;i++){   //循环条件可以进一步限制为：m-k+i<=n
        ans[k] = i;    //第k个数用i，记录到ans数组中  
        dfs(k+1);      //在第k个数用i的基础上，继续搜索第k+1个数用哪一个数字 
    }
} 
int main(){
    cin>>n>>m;
    //主函数只需要调用dfs(1)，以“考虑第1个数用哪一个数”为搜索起点 
    dfs(1); 
    return 0;
} 

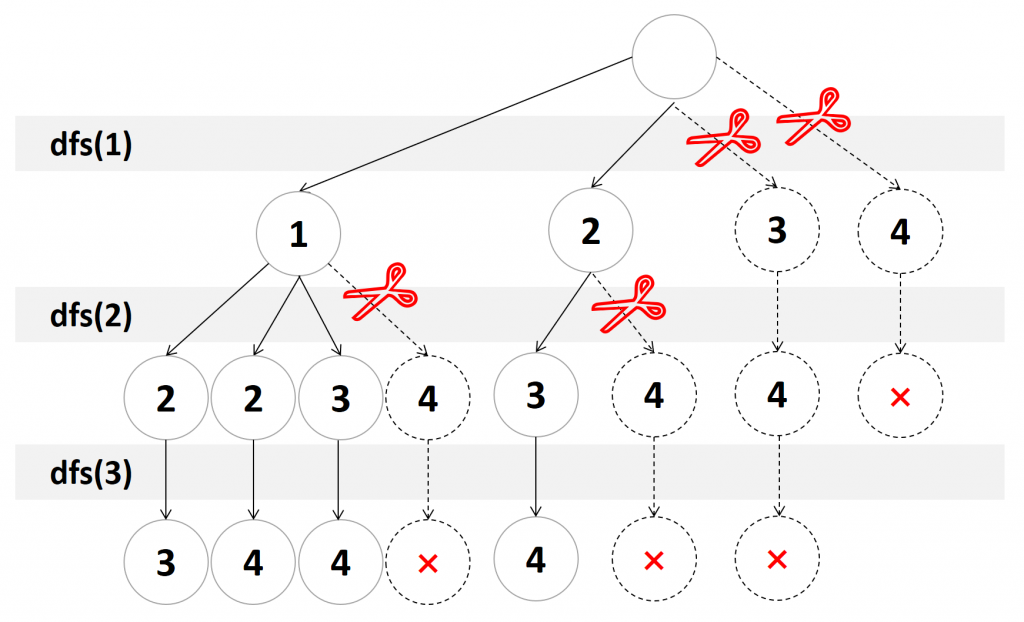
代码中函数递归所属循环处额外加了一句注释：循环的条件可以由i<=n，进一步限制为m-k+i<=n。很明显，进一步限制后循环执行的次数较少了，也就是用更严格的循环条件m-k+i<=n实现了剪枝，为什么可以这样做呢？以 \(n=4,m=3\) 为例，看下图分析：

\(dfs(k)\) 当 \(ans[k]\) 取值 \(i\)，此时如果提前发现 \(i+1\)～\(n\) 之间不足 \(m-k\) 个数，那么可知继续搜索下去是不能凑齐 \(m\) 个数的，所以 \(ans[k]\) 取值 \(i\) 并继续搜索的条件是 \(n-(i+1)-1 \ge m-k\)，也就是 \(m-k+i \le n\)。上图形象化地展示了“剪枝”的过程，如果 \(n,m\) 足够大时，剪枝的效果会更加明显。

二、素数环

问题：从1～\(n\) 中选择所有数围成一个圈环，要求任意相邻的两个数的和是一个素数，输出方案数。

分析：从1～\(n\) 中选择所有数围成一个圈环，可以认为是 \(n\) 个数的全排列，为了让结果不出现重复（例如 \(n=4\) 时，[1,2,3,4 ]和 [2,3,4,1]、[3,4,1,2]、[4,1,2,3] 均为同一种素数环，可知重复的情况其实是由一种结果顺次移位产生），可以人为指定第一个数必须是 1。

#include<iostream>
using namespace std;
const int MAX = 20;
int n,cnt = 0;
int ans[MAX+1],used[MAX+1];

//判断m是否为素数 
bool isPrime(int m){
	for(int i=2;i*i<=m;i++){
		if(m%i==0) return false;
	}
	return true;
}

//搜索第k个数用哪一个数 
void dfs(int k){
    if(k==n+1){
    	//判断是否满足相邻两个数的和是素数 
    	int f = 1;
    	ans[0] = ans[n];
    	for(int i=0;i<n;i++){
    		if(!isPrime(ans[i]+ans[i+1])){
    			f = 0;
    			break;
			}
		}
		cnt += f;
    	return;	
	}
	for(int i=2;i<=n;i++){
		if(!used[i]){
			used[i] = 1;
			ans[k] = i;
			dfs(k+1);
			used[i] = 0;
		}
	}
} 
int main(){
    cin>>n; 
    ans[1] = 1;
    dfs(2);
    cout<<cnt<<endl;
    return 0;
} 

算法的时间复杂度是 \(O((n-1)!)\)，所以当输入 \(n\) 超过 12 时，很容易就超时了。其实在搜索过程中，每次搜索的是第 \(k\) 个数究竟用哪一个数，在判断 ans[k] 是否可以取值 i 时，还可以提前判断 ans[k-1]+i 是否是素数，如果不是素数，那么就没有继续搜索下去的意义了。这是典型的剪枝策略：

#include<iostream>
using namespace std;
const int MAX = 20;
int n,cnt = 0;
int ans[MAX+1],used[MAX+1];
int prime[2*MAX+1];

//筛选法求素数 
void selectPrime(){
	for(int i=2;i*i<=2*n;i++){
		if(!prime[i])
			for(int j=i+i;j<=2*n;j+=i) prime[j]=1;
	}
}

//搜索第k个数用哪一个数 
void dfs(int k){
    if(k==n+1){
		cnt += 1-prime[ans[1]+ans[n]];
    	return;	
	}
	for(int i=2;i<=n;i++){
		if(!used[i] && prime[ans[k-1]+i]==0){
			used[i] = 1;
			ans[k] = i;
			dfs(k+1);
			used[i] = 0;
		}
	}
} 
int main(){
    cin>>n;
    selectPrime();
    ans[1] = 1;
    dfs(2);
    cout<<cnt<<endl;
    return 0;
} 

运行程序还可以发现，当 \(n\) 为奇数时，组成素数环的方案是为 0，还可以通过特判进一步提高效率。

三、走迷宫求途径最小坐标点数

仍然是前面走迷宫问题，要求解途径最小坐标点数，在递归调用前可以再添加一个条件，那就是 k+1<minstep，k+1 就是途径坐标点数量，如果发现 k+1 不小于当前搜索到的途径最小坐标点数 minstep，那么再搜索下去也就没有意义了：

#include<iostream>
using namespace std;
const int MAX = 10; 
//迷宫尺寸 
int n,m; 
//起点坐标(sx,sy)，终点坐标(fx,fy) 
int sx,sy,fx,fy;
//ans记录方案数 
int ans = 0;
//minstep记录路径途径最少坐标点数 
int minstep; 
//space数组记录迷宫里所有点的情况：1-障碍，0-通畅 
int space[MAX][MAX]; 
//used数组记录搜索过程中点是否被使用过 
int used[MAX][MAX];
//四个方向移动x,y变化值 
int dirs[4][2] = {
    {-1,0},
    {0,-1},
    {1,0},
    {0,1}
};

//从坐标点(x,y)开始搜索第k步走法
void dfs(int x,int y,int k){
    if(x==fx && y==fy){    //到达终点，方案数+1 
        ans++;
        if(k<minstep) minstep = k;
        return;
    }
    //对四个方向搜索 
    for(int i=0;i<4;i++){
        //计算下一个坐标点 
        int nx = x+dirs[i][0];
        int ny = y+dirs[i][1];
        //坐标点(nx,ny)在迷宫内、不是障碍、没有被使用过 
        if(nx>=1 && nx<=n && ny>=1 && ny<=m &&
                !space[nx][ny] && !used[nx][ny] && k+1<minstep){
            used[nx][ny] = 1;    //标记被使用
            dfs(nx,ny,k+1);      //对坐标点(nx,ny)继续展开搜索 
            used[nx][ny] = 0;    //恢复为没有被使用 
        }
    } 
} 
int main(){
    int t,x,y;
    
    cin>>n>>m>>t;
    cin>>sx>>sy>>fx>>fy;
    
    minstep = n*m; 
    
    //标记障碍 
    while(t--){
        cin>>x>>y;
        space[x][y] = 1;
    }
    
    used[sx][sy] = 1;    //标记起点被使用 
    dfs(sx,sy,1);        //从起点开始搜索第1步走法 
    
    cout<<(ans?minstep:-1)<<endl;
    return 0;
} 

对于DFS算法，当数据规模超过几十个时，往往会出现超时，如果能够有效剪枝，那么可能会避免超时的情况。后面介绍动态规划的背包问题模型可以更加高效地解决一些采用DFS算法会超时的问题。