接下来介绍另一种搜索算法——广度优先搜索(BFS,有时候又称之为宽度优先搜索)。广度优先搜索比深度优先搜索简单,也更容易理解。如果一个问题两种搜索策略都能解决,一般情况推荐使用广度优先搜索,因为广度优先搜索的时间复杂度一般会低于深度优先搜索。
一、广度优先搜索
仍然来看跳马问题:P1443 马的遍历
对于 \(n \times m\) 的棋盘,马位于 \((x,y)\),计算马跳到棋盘上每一点至少需要的步数。
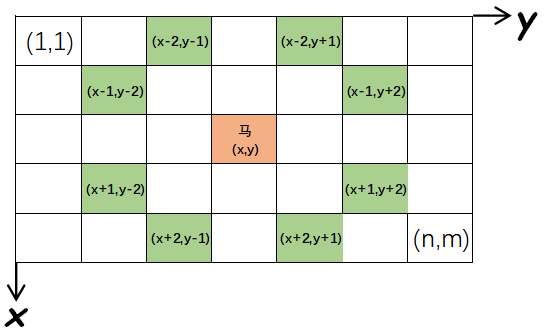
仔细读题,特别是分析输入输出样例,可以得出题目中设定的坐标系和马的跳法如下图所示:
显然,使用DFS来搜索 \((x,y)\) 到棋盘上每一点的最短跳法是很容易超时的,这里用广度优先搜索(BFS)来解决。使用广度优先搜索,与初始状态越接近的情况会优先搜索到,例如本题中从 \((x,y)\) 出发,使用广度优先搜索策略,首先搜索到的是跳 1 步能够到达的所有点,接着搜索到的是跳 2 步能够到达的所有点,……,就这样依次搜索下去,直到没有符合条件的点为止(所有点都被搜索过了)。
和DFS一样,BFS也有固定的结构,一般借助队列结构来实现BFS。首先将初始状态(例如本题中的初始点坐标)入队到空队列中,然后每次取出队首并出队,找出队首能转移到的所有状态(例如本题中马能跳到的所有点的坐标,当然要排除掉已经搜索过的点),将这些满足条件的状态全部入队。如此反复操作,直到队列为空为止。这样做就能保证从初始状态搜索到任意状态时一定是最短路径(例如本题中的最少步数)。
广度优先搜索的一般结构如下:
void bfs(){
初始状态入队;
while(队列不为空){
取出队首;
出队;
//if(取出的队首是目标状态) return;
for(枚举由取出的队首出发能够到达的所有状态){
if(满足条件){ //例如该状态还没有被搜索过
当前状态入队;
}
}
}
}
void bfs(){
初始状态入队;
while(队列不为空){
取出队首;
出队;
for(枚举由取出的队首出发能够到达的所有状态){
if(满足条件){ //例如该状态还没有被搜索过
//if(当前枚举的是目标状态) return;
当前状态入队;
}
}
}
}
这里先给出参考代码,然后结合代码说明BFS的搜索过程:
#include<cstdio>
#include<cstring>
using namespace std;
const int MAX = 400;
//用结构体表示坐标
struct Point{
int x,y;
Point(){}
Point(int x,int y){
this->x = x;
this->y = y;
}
};
int n,m,x,y;
int ans[MAX+1][MAX+1]; //记录到每一点的最小步数
int dirs[8][2]={ //马8种跳法x,y坐标增量
{2,1},
{1,2},
{-1,2},
{-2,1},
{-2,-1},
{-1,-2},
{1,-2},
{2,-1}
};
/****************************************************************/
//使用数组模拟“队列”
Point queue[MAX*MAX+10]; //极限情况是全部点都要入队,这里开到MAX*MAX+10足够用了
int front = 0; //队首“指针”,也就是队首对应数组的下标
int rear = 0; //队尾“指针”,其实是下一个入队元素存放位置(真实队尾应该是rear-1)
void push(Point p){ //入队
queue[rear++] = p;
}
void pop(){ //出队
front++;
}
Point getfront(){ //取队首元素
return queue[front];
}
bool empty(){ //判断队列是否为空
return front==rear;
}
/****************************************************************/
void bfs(){
push(Point(x,y));
ans[x][y] = 0; //起点跳跃步数为0
while(!empty()){
Point p = getfront();
pop();
int d = ans[p.x][p.y]; //跳到(p.x,p.y)的步数
//枚举考查8个方向的跳跃
for(int i=0;i<8;i++){
int nx = p.x+dirs[i][0];
int ny = p.y+dirs[i][1];
//在棋盘内,并且还没有被搜索过(ans[nx][ny]没有被修改过,仍然是初始值-1)
if(nx>=1 && nx<=n && ny>=1 && ny<=m && ans[nx][ny]==-1){
ans[nx][ny] = d+1; //从(p.x,p.y)跳来,步数+1
push(Point(nx,ny));
}
}
}
}
int main()
{
//将所有点跳跃步数赋值为-1(正好与题目中不能跳到某一点用-1输出吻合)
//在深度优先搜索中如果搜到某点发现该点跳跃步数为-1,证明该点没有被搜索过
memset(ans,-1,sizeof(ans));
scanf("%d%d%d%d",&n,&m,&x,&y);
bfs();
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++) printf("%-5d",ans[i][j]);
printf("\n");
}
return 0;
}
以 \(n=4,m=4,x=1,y=1\) 为例,广度优先搜索的具体过程如下:
- 搜索前准备工作,记录到每个点最少步数的二维数组ans 所有元素值赋值为 -1;
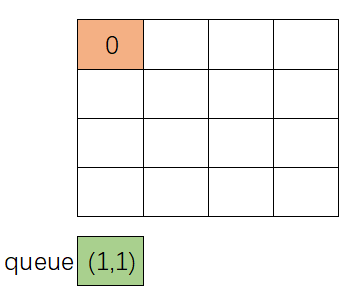
- 队列初始为空队列,起始点 \((x,y)\)(也就是 \((1,1)\))入队(
push(Point(x,y))),起始点跳跃步数设置为 0(ans[x][y]=0)。下图中如果将表格认为是 ans 数组的话,空白处值均为特殊初值 -1;
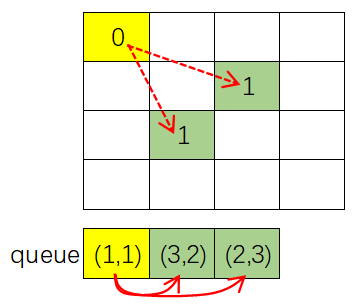
- 取出队首元素并出队,取出来的元素坐标为 \((1,1)\),该点的最小跳跃步数是 d=ans[1][1](值为 0),考查该点 8 个方向跳跃的下一点,有 2 个点 \((3,2)\) 和 \((2,3)\) 在棋盘内,并且这两个点都没有搜索过(ans[3][2] 和 ans[2][3] 值均为特定初始值 -1),可知这两点都符合条件:将 ans[3][2] 和 ans[2,3] 均赋值为 d+1(也就是1),并且这两点入队;
- 取出队首元素并出队,取出来的元素坐标为 \((3,2)\),该点的最小跳跃步数是 d=ans[3][2](值为 1),考查该点 8 个方向跳跃的下一点,有 4 个点 \((4,4)\)、\((2,4)\)、\((1,3)\)、\((1,1)\) 在棋盘内,但只有 3 个点没有搜索过(ans[4][4]、ans[2][4]、ans[1][3] 值均为特定初始值 -1,ans[1][1] 值为 0 不等于 -1),可知这 3 点都符合条件:将 ans[4][4]、ans[2][4]、ans[1][3] 均赋值为 d+1(也就是 2),并且这 3 点入队;
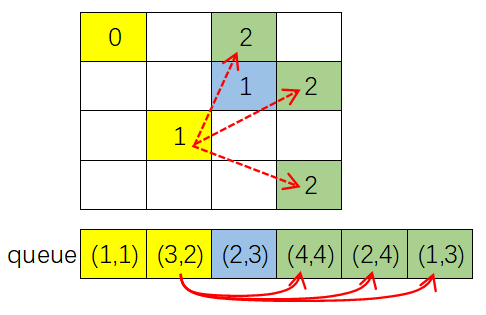
- 取出队首元素并出队,取出来的元素坐标为 \((2,3)\),该点的最小跳跃步数是 d=ans[2][3](值为1),考查该点 8 个方向跳跃的下一点,有 2 个点 \((3,1)\) 和 \((4,2)\) 在棋盘内且没有搜索过(ans[3][1]、ans[4][2] 值均为特定初始值 -1,另外两个在棋盘内的点 ans[4][4]、ans[1][1] 值不等于 -1 表明前面搜索过),可知这 2 点都符合条件:将 ans[3][1]、ans[4][2] 均赋值为 d+1(也就是 2),并且这 2 点入队;
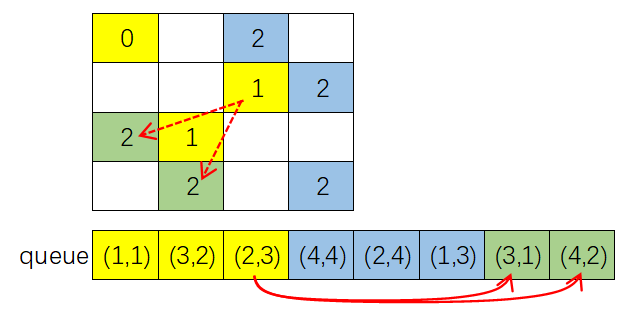
- 取出队首元素并出队,取出来的元素坐标为 \((4,4)\),该点的最小跳跃步数是 d=ans[4][4](值为 2),考查该点 8 个方向跳跃的下一点,发现 2 个点在棋盘内但是都搜索过。本次没有任何点入队;
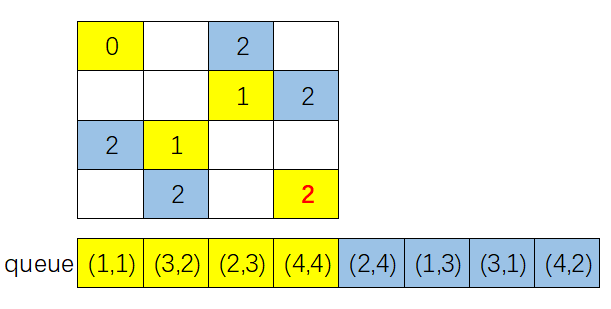
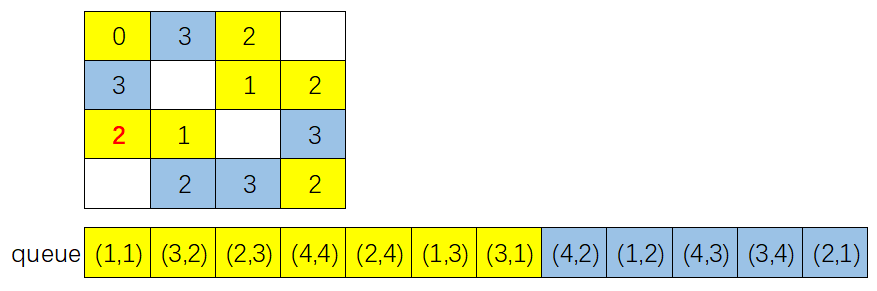
- 取出队首元素并出队,取出来的元素坐标为 \((2,4)\),该点的最小跳跃步数是 d=ans[2][4](值为 2),考查该点 8 个方向跳跃的下一点,有 2 个点 \((1,2)\) 和 \((4,3)\) 在棋盘内且没有搜索过(ans[1][2]、ans[4][3] 值均为特定初始值 -1,另外 1 个在棋盘内的点 ans[3][2] 值不等于 -1 表明前面搜索过),可知这 2 点都符合条件:将 ans[1][2]、ans[4][3] 均赋值为 d+1(也就是 3),并且这 2 点入队;
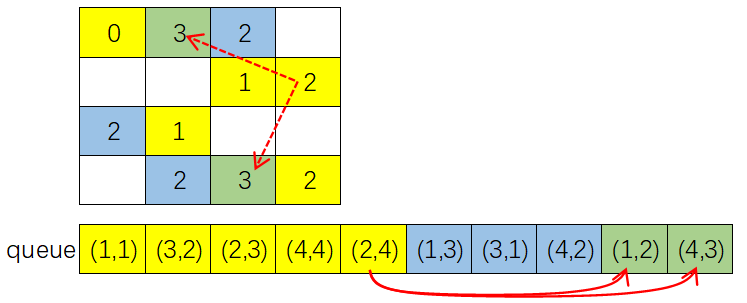
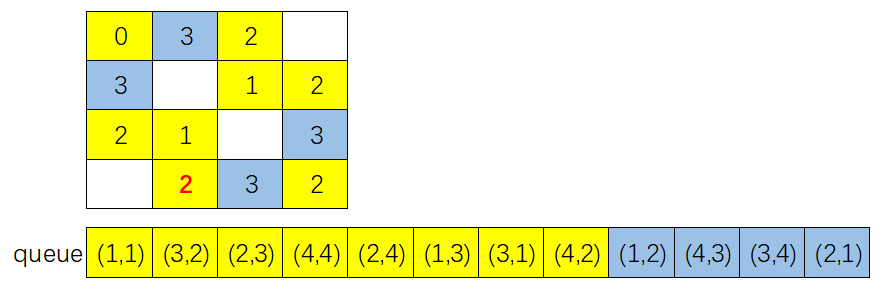
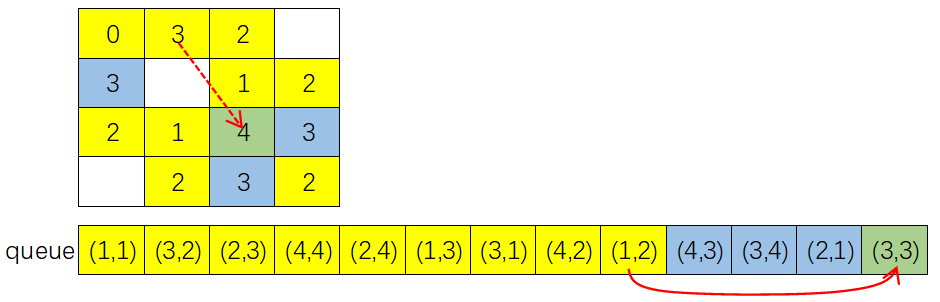
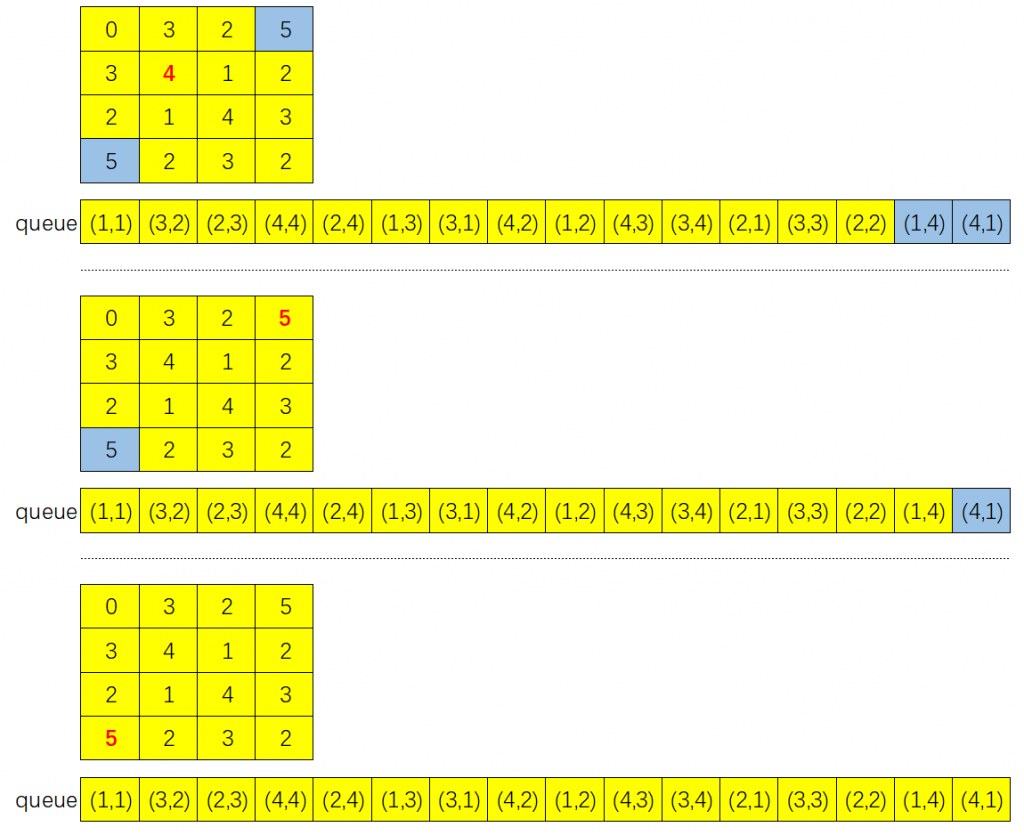
- 剩下步骤给出图示,读者可以自行分析:





二、广搜与深搜
上面问题,广度优先搜索的过程还可以用下图表示:
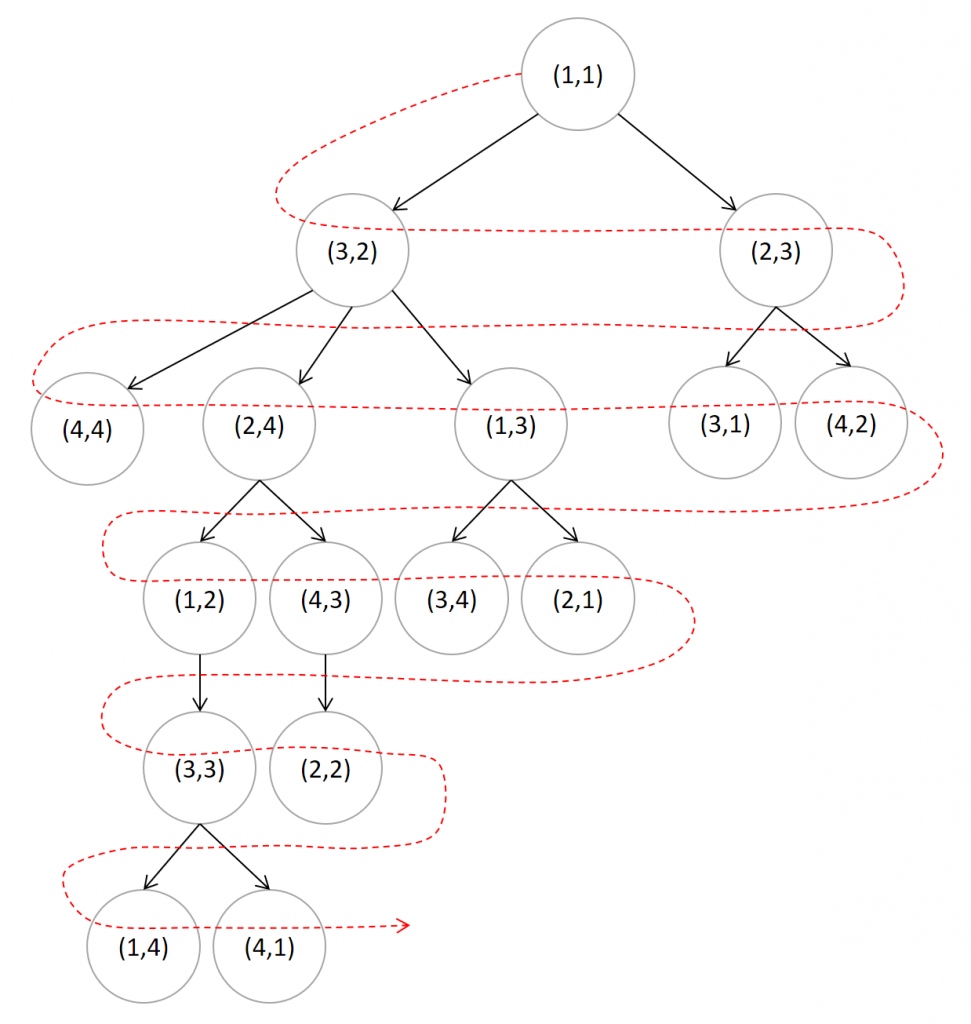
上图这样描述搜索过程的方法称为解答树。从解答树可以直观看出,广度优先搜索从起点开始,依次扩展。先扩展所有近处的结点,然后再依次扩展比较远的结点,而不像深度优先搜索那样沿着一条路径一直往前走到头。基于这个特性,广度优先搜索适合解决寻找步骤最少、距离最近的的问题,空间代价是需要额外维护一个队列来存储搜索到的结点信息。而深度优先搜索适合求解具体方案或者特殊要求操作步骤满足字典序的问题。
三、使用STL中的queue队列
广度优先搜索需要维护一个队列,实际编程时推荐使用 STL(标准模板库)中的队列 queue。STL 中的队列 queue 其实是一个模板类,提供了队列的一系列方法,比起前面使用数组来模拟队列,使用 STL 中的队列 queue 的话操作会更加便捷。后面会详细介绍 STL,这里简单介绍 queue 的使用:
- 引入头文件:
#include<queue> - 定义一个队列:
queue<int> Q;定义了一个元素均为 int 的队列 Q,queue<Point> Q;定义了一个元素均为自定义结构体 Point 的队列 Q; - 入队:
Q.push(要入队的元素);例如Q.push(123);将整数123入队到元素为 int 的队列 Q 中;Q.push(Point(x,y));将构造函数Point(x,y)生成的Point实例入队到元素为 Point 的队列 Q 中; - 取队首元素:
Q.front();例如Point p = Q.front();将队首的元素取出来赋值给 Point 类型变量 p; - 出队:
Q.pop(); - 判断队列为空:
if(Q.empty()){ }
上面的程序改写成使用 STL 中的队列 queue 的参考代码如下:
#include<cstdio>
#include<queue>
#include<cstring>
using namespace std;
const int MAX = 400;
//用结构体表示坐标
struct Point{
int x,y;
Point(){}
Point(int x,int y){
this->x = x;
this->y = y;
}
};
int n,m,x,y;
int ans[MAX+1][MAX+1]; //记录到每一点的最小步数
int dirs[8][2]={ //马8种跳法x,y坐标增量
{2,1},
{1,2},
{-1,2},
{-2,1},
{-2,-1},
{-1,-2},
{1,-2},
{2,-1}
};
/****************************************************************/
//使用STL中的模板类queue实现队列
queue<Point> Q;
/****************************************************************/
void bfs(){
Q.push(Point(x,y));
ans[x][y] = 0; //起点跳跃步数为0
while(!Q.empty()){
Point p = Q.front();
Q.pop();
int d = ans[p.x][p.y]; //跳到(p.x,p.y)的步数
//枚举考查8个方向的跳跃
for(int i=0;i<8;i++){
int nx = p.x+dirs[i][0];
int ny = p.y+dirs[i][1];
//在棋盘内,并且还没有被搜索过(ans[nx][ny]没有被修改过,仍然是初始值-1)
if(nx>=1 && nx<=n && ny>=1 && ny<=m && ans[nx][ny]==-1){
ans[nx][ny] = d+1; //从(p.x,p.y)跳来,步数+1
Q.push(Point(nx,ny));
}
}
}
}
int main()
{
//将所有点跳跃步数赋值为-1(正好与题目中不能跳到某一点用-1输出吻合)
//在深度优先搜索中如果搜到某点发现该点跳跃步数为-1,证明该点没有被搜索过
memset(ans,-1,sizeof(ans));
scanf("%d%d%d%d",&n,&m,&x,&y);
bfs();
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++) printf("%-5d",ans[i][j]);
printf("\n");
}
return 0;
}
 NOIP学习小站
NOIP学习小站