一、queue简介
前面已经介绍过队列(线性表——队列),队列(queue)是一种典型的FIFO(first in first out,先进先出)线性表结构,STL中有专门的queue容器。其实queue是一种容器适配器,默认情况下内部是基于deque容器实现的。
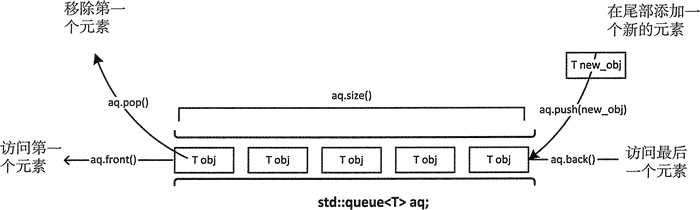
要使用queue,需要先包引入头文件#include<queue>。queue同样也有和stack类似的push()、pop()成员函数。区别在于,queue的push()发生在队尾,pop()发生在队首。此外,还有front()返回队首元素,back()返回队尾元素。
#include<iostream>
#include<queue>
using namespace std;
int main()
{
queue<int> q;
cout<<q.size()<<endl; //队列元素数量
q.push(1); //入队
q.push(2); //入队
cout<<q.front()<<endl; //取队首元素
cout<<q.back()<<endl; //取队尾元素
q.pop(); //出队
cout<<q.front()<<endl;
cout<<q.back()<<endl;
for(int i=1;i<=10;i++) q.push(i);
//所有元素出队
while(!(q.empty())){
cout<<q.front()<<" ";
q.pop();
}
cout<<endl;
//判断队列是否为空
if(q.empty()) cout<<"empty"<<endl;
return 0;
}
因为队列LIFO的特点,常将queue用于广度优先搜索。
二、经典例题
1.约瑟夫问题
可以用队列解决约瑟夫问题,每次数数,就是前\(m-1\)个人从队首依次来到队尾,然后第\(m\)个人出队:
#include<iostream>
#include<queue>
using namespace std;
int main()
{
queue<int> q;
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++) q.push(i);
while(!(q.empty())){
//m-1人从队首来到队尾(取出队首元素入队,队首元素出队)
for(int i=1;i<m;i++){
q.push(q.front());
q.pop();
}
//输出队首元素
cout<<q.front()<<" ";
//第m个人(正好在队首)出队
q.pop();
}
return 0;
}
2.Blah数集
大数学家高斯小时候偶然间发现一种有趣的自然数集合 Blah,对于以 a 为基的集合 Ba 定义如下:
(1) a 是集合 Ba 的基,且 a 是 Ba 的第一个元素;
(2) 如果 x 在集合 Ba 中,则 2x+1 和 3x+1 也都在集合 Ba 中;
(3) 没有其他元素在集合 Ba 中了。
现在提供 a 和 N,小高斯想知道如果将集合 Ba 中元素按照升序排列,第 N 个元素会是多少?
【思路】对于最开始的 a,产生的两个新元素放入到队列中,从队列里取出最小的数再产生新的两个元素,……这样的话,要考虑如何从队列中找最小的元素,并且还要避免产生重复的数,这两个问题都不容易处理。其实可以用三个队列,队列 q 用来记录产生的数,队列 q2 用来记录 2x+1 规则产生的数,队列 q3 用来记录 3x+1 规则产生的数,取 q 的队头元素记为 x,那么将 2x+1 入队列 q2,将 3x+1 入队列 q3,然后将 q2 队首和 q3 队首较小的那个数入队列 q,这样就可以保证 q 中的元素一直从小到大排列,并且不会出现重复。
#include<iostream>
#include<queue>
using namespace std;
int main()
{
int a,n;
cin>>a>>n;
queue<long long> q2,q3,q;
q.push(a);
int i;
for(i=1;i<n;i++){
q2.push(q.front()*2+1); //2x+1 入队q2
q3.push(q.front()*3+1); //3x+1 入队q3
q.pop();
//q新入队元素 是 q2和q3较小的队首元素
if (q2.front() < q3.front()) //q2队首元素小
q.push(q2.front()),q2.pop();
else if (q2.front() > q3.front()) //q3队首元素小
q.push(q3.front()),q3.pop();
else //q2和q3队首元素相等
q.push(q2.front()),q2.pop(),q3.pop(); //q2,q3均出队,避免重复
}
cout<<q.front()<<endl;
return 0;
}
不用队列也能解决问题,请分析体会下面的程序:
#include<iostream>
using namespace std;
long long p[1000100]; //存储结果
long long blah(int a,int n){
p[1] = a; //第一个元素
//t是新元素记录到数组的位置
//t1是记录x*2+1规则产生新元素的x所在下标
//t2是记录x*3+1规则产生新元素的x所在下标
int t = 1,t1 = 1,t2 = 1; //三个下标
while(t<n){
long long x = p[t1]*2+1; //一种是乘2加1
long long y = p[t2]*3+1; //另外一种是乘3加1
//x,y只有3种情况
if(x>y)
p[++t] = y,t2++;
else if(y>x)
p[++t] = x,t1++;
else
p[++t] = x,t1++,t2++;
}
return p[t];
}
int main(){
int a,n;
cin>>a>>n;
cout<<blah(a,n)<<endl;
return 0;
}
3.广度优先搜索
可以查看这里:
三、优先队列priority_queue
普通的队列queue是一种先进先出的数据结构,元素在队列尾追加,而从队首删除。在优先队列priority_queue中,元素被赋予优先级——当访问元素时,具有最高优先级的元素最先访问或者删除。优先队列具有最高级先出(first in largest out)的行为特征。priority_queue可以用vector或deque实现,默认情况下用vector实现。
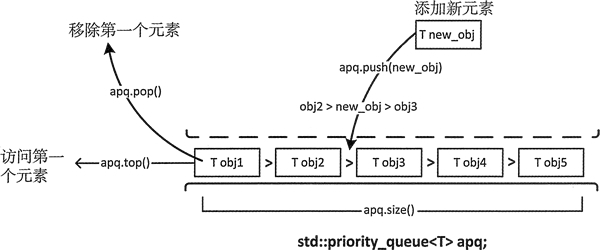
priority_queue默认的元素比较器是less <T>。也就是说,在默认情况下,要放入priority_queue的元素必须是能用“<”运算符进行比较的(如果是结构体可以重载<运算符),而且priority _queue保证以下条件总是成立:对于队首的元素 \(x\) 和任意非队首的元素 \(y\),表达式 \(x<y\) 必为false。
priority_queue是使用“堆排序”技术实现的,其内部并非完全有序,但却能确保最优元素总在队首。因此,priority_queue特别适用于“不停地在一堆元素中取走最优的元素”这种情况。priority_queue插入和删除元素的复杂度都是\(O(log(n))\)。
1.申明优先队列
要使用priority_queue,同样需要引入头文件#include<queue>。简单地申明优先队列时,其内部是基于vector实现的,默认是大根堆,也就是队首元素比其他元素都大:
priority_queue<int> pq; //申明优先队列,默认是大根堆(队首元素比其他元素都大)
也可以指定优先队列的内部实现容器,还可以提供一个比较函数(仿函数)来确定优先队列的优先规则:
//优先队列内部使用vector实现,比较函数是less<int>(优先队列默认比较函数就是less<T>),这里是大根堆 priority_queue<int,vector<int>,less<int> > pq1; //优先队列内部使用vector实现,比较函数是greater<int>,这里是小根堆(队首元素比其他元素都小) priority_queue<int,vector<int>,greater<int> > pq2;
上面使用的less<T>和greater<T>都是C++内置的两个“仿函数”,其实可以通过结构体来自定义仿函数:
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
struct Point{
double x,y;
Point(double x,double y){
this->x = x;
this->y = y;
}
};
//通过结构体自定义类似于less<T>和greater<T>的仿函数
struct cmp{
bool operator ()(const Point &a,const Point &b){
return a.x*a.x+a.y*a.y<b.x*b.x+b.y*b.y;
}
};
int main()
{
priority_queue<Point,vector<Point>,cmp> pq;
return 0;
}
使用仿函数定义优先队列大根堆/小根堆区别方法:如果仿函数用来排序是升序排序,那么用来作为优先队列的优先级规则时是大根堆(队首是排序结果的最大元素),和排序结果正好相反。
对于元素是结构体的情况,还可以重载结构体运算符来申明优先队列:
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
struct Point{
double x,y;
Point(double x,double y){
this->x = x;
this->y = y;
}
void print() const{
cout<<"("<<x<<","<<y<<")";
}
};
//比较规则:坐标点到原点的距离
bool operator < (const Point &a,const Point &b){
return a.x*a.x+a.y*a.y<b.x*b.x+b.y*b.y;
}
bool operator > (const Point &a,const Point &b){
return a.x*a.x+a.y*a.y>b.x*b.x+b.y*b.y;
//return b<a; 亦可
}
int main()
{
//大根堆,需要使用到Point结构体重载的<运算
priority_queue<Point> pq1;
//priority_queue<Point,vector<Point>,less<Point> > pq1;
//小根堆,需要使用到Point结构体重载的>运算
priority_queue<Point,vector<Point>,greater<Point> > pq2;
double arrxy[5] = {1.2,2.3,3.4,4.5,5.6};
for(int i=0;i<5;i++){
pq1.push(Point(arrxy[i],arrxy[i]));
pq2.push(Point(arrxy[i],arrxy[i]));
pq1.top().print();
cout<<" ";
pq2.top().print();
cout<<endl;
}
return 0;
}
priority_queue的成员函数和queue类似,不过没有front()和back(),取队首元素的成员函数是top()。
2.经典例题:priority queue练习题
问题见NOI OpenJudge:OpenJudge - 3345:priority queue练习题

可以申明两个优先队列,分别是大根堆和小根堆,每次操作过程中所有元素入队后再取队首元素并出队,可知每次取出的队首元素就是题目要求的优先级最高和最低的元素。
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
struct Num{
int n; //数字本身
int k; //质因数数量
Num(int n){
this->n = n;
k = 0;
int i = 2,t = n;
while(t!=1){
if(t%i==0){
if(i!=n) k++;
while(t%i==0) t/=i;
}
i++;
}
}
};
bool operator < (const Num &a,const Num &b){
if(a.k==b.k) return a.n<b.n;
return a.k<b.k;
}
bool operator > (const Num &a,const Num &b){
return b<a;
}
priority_queue<Num> pq1;
priority_queue<Num, vector<Num>, greater<Num> > pq2;
int main()
{
int n,m;
cin>>n;
//n次操作
while(n--){
//每次10个元素入队
for(int i=1;i<=10;i++){
cin>>m;
pq1.push(Num(m));
pq2.push(Num(m));
}
//取队首元素输出
cout<<pq1.top().n<<" "<<pq2.top().n<<endl;
//出队
pq1.pop();
pq2.pop();
}
return 0;
}
 NOIP学习小站
NOIP学习小站